Normalkraft
Normalkraften är den kraft som marken (eller någon annan yta) trycker uppåt med. Om det inte fanns någon normalkraft skulle du sakta sjunka ner i marken.
Normalkraften på ett föremål är alltid vinkelrät (i rät vinkel) mot den yta som föremålet befinner sig på.
På en plan yta är ett föremåls normalkraft m g {\displaystyle mg} 
(föremålets vikt, dvs. dess massa multiplicerad med gravitationskraften).
På ett lutande plan minskas normalkraften med vinkeln, och normalkraften är m g c o s θ {\displaystyle mgcos\theta } 
.
Observera att på en plan yta skulle θ {\displaystyle \theta }
vara 0, och därför skulle c o s θ {\displaystyle cos\theta }
vara 1. De två ekvationerna är alltså lika.
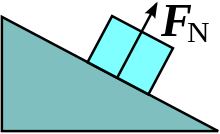
FN representerar normalkraften.
Frågor och svar
F: Vad är normalkraft?
A: Normalkraften är den kraft som marken (eller någon annan yta) trycker tillbaka uppåt med.
F: Vad skulle hända om det inte fanns någon normalkraft?
S: Om det inte fanns någon normalkraft skulle du långsamt sjunka ner i marken.
F: Hur hänger normalkraften på ett föremål samman med dess vikt?
S: På en plan yta är ett föremåls normalkraft lika med dess vikt (föremålets massa multiplicerad med gravitationskraften).
F: Hur påverkar ett lutande plan normalkraften?
S: På ett lutande plan minskar normalkraften med vinkeln, och den kan beräknas med hjälp av m g c o s θ.
F: Vad representerar θ i denna ekvation?
S: θ representerar lutningsvinkeln i denna ekvation.
F: När skulle cosθ vara 1?
S: cosθ skulle vara 1 när θ (vinkeln)är 0, vilket sker på en plan yta.
Fråga: Hur förhåller sig dessa två ekvationer till varandra? S: De två ekvationerna är lika när de är på en plan yta.
