Quicksort
Quicksort är en sorteringsalgoritm som används för att sortera element i en array. Den skapades av Tony Hoare 1959 och används fortfarande flitigt idag. Quicksort skapar partitioner i matrisen, vilket i huvudsak innebär att den delar matrisen i två delar och sedan fortsätter att dela upp dessa delar i fler delar och sorterar längs vägen. Den gör själva sorteringen genom att det är en jämförelsesort. Detta innebär att den väljer en central punkt i matrisen och jämför den sedan med alla andra punkter i matrisen.
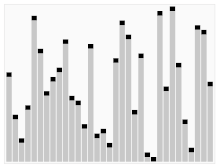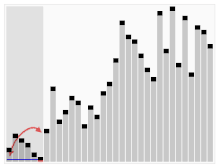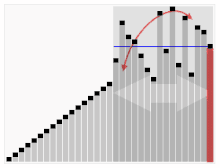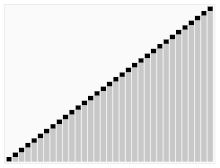
Animerad visualisering av quicksort-algoritmen. De horisontella linjerna är pivotvärden.
Algoritm
- Välj vilket element som helst i matrisen, detta blir nu vridpunkten.
- Dela upp elementen. Jämför alla element i matrisen med pivot, de som är lägre än pivot flyttas till vänster om pivot, och alla element i matrisen som är högre än pivot flyttas till höger om pivot. Observera att vår pivot nu befinner sig i sin sorterade position.
- Återfinns i de två partitionerna. Tillämpa ovanstående två steg på de två partitioner som vi skapade i steg 2.
Ofta väljs det mest vänstra elementet som pivot. Rekursionen innebär att algoritmen kör exakt samma algoritm på de två partitioner som skapats genom jämförelserna med pivot. Observera att denna algoritm fortsätter att dela upp matrisen i delmatriser och dela upp dessa delmatriser i ännu mindre delmatriser. Varje gång den gör detta kommer den att välja en ny pivot inom delmängden och jämföra elementen med delmängden. Basfallet är när algoritmen når en delmall med endast ett element, där den bara stannar eftersom ett element inte behöver sorteras.
