Theorema egregium
Gauss' Theorema Egregium (latin för "anmärkningsvärd sats") är ett viktigt resultat inom differentialgeometrin som bevisades av Carl Friedrich Gauss. Teoremet handlar om ytors krökning. Enligt teoremet kan krökningen bestämmas enbart genom att mäta vinklar, avstånd och deras hastighet på en yta. Det finns inget behov av att tala om det särskilda sätt på vilket ytan är inbäddad i det omgivande tredimensionella euklidiska rummet. Med andra ord förändras inte den gaussiska krökningen av en yta om man böjer ytan utan att sträcka ut den.
Gauss presenterade satsen på följande sätt (översatt från latin):
Av denna anledning leder formeln i föregående artikel till den anmärkningsvärda satsen. Om en krökt yta utvecklas på vilken annan yta som helst, förblir krökningsmåttet i varje punkt oförändrat.
Satsen är "anmärkningsvärd" eftersom den ursprungliga definitionen av gaussisk krökning direkt utnyttjar ytans position i rummet. Det är därför ganska förvånande att resultatet inte beror på dess inbäddning trots alla böjnings- och vridningsdeformationer som genomgåtts.
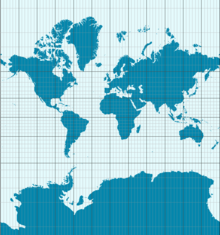
En konsekvens av Theorema Egregium är att jorden inte kan visas på en karta utan att den förvrängs. Mercatorprojektionen, som visas här, bevarar vinklarna men ändrar ytan. Som ett exempel visas Antarktis mycket större än vad det egentligen är.
Frågor och svar
Fråga: Vad är Gauss Theorema Egregium?
S: Gauss Theorema Egregium är ett viktigt resultat inom differentialgeometri som handlar om ytors krökning, bevisat av Carl Friedrich Gauss.
F: Hur kan krökningen bestämmas, enligt Gauss teorem Egregium?
S: Enligt Gauss Theorema Egregium kan krökningen bestämmas enbart genom att mäta vinklar, avstånd och deras hastighet på en yta.
F: Är det nödvändigt att tala om det speciella sätt på vilket ytan är inbäddad i den omgivande tredimensionella euklidiska rymden för att bestämma krökningen?
S: Nej, det är inte nödvändigt att tala om det särskilda sätt på vilket ytan är inbäddad i den omgivande tredimensionella euklidiska rymden för att bestämma krökningen enligt Gauss teorema Egregium.
F: Ändras den gaussiska krökningen hos en yta om man böjer ytan utan att sträcka ut den?
S: Nej, den Gaussiska krökningen av en yta ändras inte om man böjer ytan utan att sträcka ut den enligt Gauss Teorema Egregium.
F: Vem presenterade satsen på detta sätt?
S: Gauss presenterade satsen på detta sätt.
F: Vad är satsen anmärkningsvärd för?
S: Satsen är "anmärkningsvärd" eftersom den inledande definitionen av gaussisk krökning direkt använder sig av ytans position i rummet. Därför är det ganska förvånande att resultatet inte beror på dess inbäddning trots alla böjande och vridande deformationer som den utsätts för.
F: På vilket sätt presenterade Gauss satsen?
S: Gauss presenterade satsen på ett sådant sätt att om en krökt yta utvecklas på någon annan yta, förblir krökningens mått i varje punkt oförändrad.
Sök