Graffärgning: definition, kromatiskt tal och grundläggande begrepp
Upptäck graffärgning i grafteori: definition, kromatiskt tal och grundläggande begrepp för att förstå hur man bestämmer och minimerar färger i grafer.
Graffärgning är namnet på ett antal problem från grafteorin. Dessa problem handlar om att färga (eller märka) hörnen i en graf under vissa förutsättningar. Ett enkelt problem i detta sammanhang kan vara att söka efter det minsta antalet färger som behövs för att färga hörnen, när två sammanhängande hörn inte kan ha samma färg. I grafen som visas kallas cirklarna för hörn och de linjer som förbinder dem kallas för kanter. Det minsta antalet färger som behövs för att färga en graf kallas dess kromatiska tal.
Definition och grundläggande begrepp
En riktig (korrekt) graffärgning är en tilldelning av färger till varje hörn så att vilka två hörn som är förbundna med en kant aldrig får samma färg. Det minsta antalet färger som behövs för en sådan korrekt färgning kallas grafens kromatiska tal och skrivs ofta χ(G).
Andra vanliga begrepp:
- Klukka (klique): en mängd hörn där alla par är förbundna. Om grafen innehåller en klikk av storlek k så gäller χ(G) ≥ k.
- Grad (degree) för ett hörn: antal kanter som går ut från hörnet. Den maximala graden i grafen skrivs ofta Δ.
- Bipartit graf: en graf utan udda cykler. En icke-tom bipartit graf har χ(G)=2. En graf utan kanter har χ(G)=1.
- Kromatisk index (edge coloring): motsvarande problem för kanter, det vill säga att färga kanter så att intilliggande kanter får olika färger.
Enkla exempel
- Komplett graf K_n: varje par hörn är förbundet, därför krävs n olika färger, så χ(K_n)=n.
- Cykliska grafer: en jämn cykel C_{2k} är bipartit och har χ=2, medan en udda cykel C_{2k+1} har χ=3.
- Stjärngraf (en nod i mitten kopplad till flera löv): har χ=2 om det finns minst en kant.
Viktiga satser och gränser
- Övre begränsning med grad: en enkel följd är att χ(G) ≤ Δ+1. En enkel färgningsalgoritm (greedy) ger denna gräns.
- Brooks sats: för en sammanhängande graf G med maximal grad Δ gäller i allmänhet χ(G) ≤ Δ, med undantag för kompletta grafer och udda cykler där χ(G)=Δ+1.
- Fyra-färgssatsen: varje plan graf kan färgas med högst 4 färger, alltså χ(G) ≤ 4 för planar grafer.
- Vizings sats (för kantfärgning): grafens kromatiska index är antingen Δ eller Δ+1.
- Kromatisk polynom: för varje graf finns ett polynom P_G(k) som räknar antalet korrekta färgningar med k färger. Det uppfyller en rekursiv formel via deletion–contraction.
Algoritmer och komplexitet
Beslutet om en graf kan färgas med högst k färger (k-graffärgningsproblemet) är i allmänhet NP-fullständigt för fasta k≥3. Det innebär att det inte finns kända effektiva algoritmer som alltid löser problemet snabbt för stora godtyckliga grafer. För speciella grafer (t.ex. träd, bipartita grafer eller planar grafer under vissa villkor) finns dock effektiva algoritmer.
Vanliga algoritmer och heuristiker:
- Greedy-algoritmen: färgar hörn i en ordning och väljer lägsta möjliga färg. Enkel men beroende av ordningen.
- DSATUR: en heuristik som successivt väljer hörnet med störst antal redan använda närliggande färger (saturation).
- Exacta metoder: backtracking, branch-and-bound och SAT-reduktioner används för små eller medelstora instanser.
Varianter och generaliseringar
- Listfärgning: varje hörn har en lista med tillåtna färger; man söker en korrekt färgning där varje hörn får en färg från sin lista.
- Fraktionell kromatisktal: en relaxation som tillåter blandningar av färgningar och ger ett rationellt värde mellan 1 och n.
- Kantfärgning: se kromatisk index och Vizings sats.
- Färgning med restriktioner: ex.vis distansfärgning där hörn inom viss avståndsgräns inte får samma färg (används i frekvensplanering).
Tillämpningar
Graffärgning används i praktiska problem som:
- Schemaläggning (tidsluckor för prov, lektioner eller jobb utan konflikter).
- Registerallokering i kompilatorer (minimera antalet register genom färgning av interferensgrafen).
- Frekvensallokering i mobilnät (minimera störningar mellan sändare).
- Pussel och spel, t.ex. Sudoku kan formuleras som en graffärgningsuppgift.
Sammanfattning
Graffärgning är ett centralt område i grafteorin med enkla definitioner men ofta svåra och intressanta frågor. Begreppet kromatiskt tal fångar hur många färger som behövs för en korrekt färgning, och både teoretiska resultat (som Brooks sats och fyra-färgssatsen) och praktiska algoritmer (greedy, DSATUR, backtracking) spelar viktiga roller när man analyserar och försöker lösa färgningsproblem.
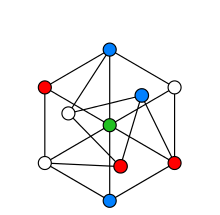
En giltig lösning för att färglägga en graf när två anslutna hörn inte får ha samma färg.
Frågor och svar
F: Vad är graffärgning?
S: Graffärgning är ett problem inom grafteori som handlar om att färga eller märka topparna i en graf enligt vissa villkor.
F: Vad är ett enkelt problem i samband med graffärgning?
S: Ett enkelt problem kan vara att hitta det minsta antalet färger som behövs för att färglägga topparna i en graf, samtidigt som man ser till att två sammanhängande toppar inte har samma färg.
F: Vad kallas cirklarna i en graf?
S: Cirklarna i en graf kallas för hörnpunkter.
F: Vad kallas linjerna som förbinder cirklarna i en graf?
S: Linjerna som förbinder cirklarna i en graf kallas för kanter.
F: Vad kallas det minsta antal färger som behövs för att färglägga en graf?
S: Det minsta antalet färger som behövs för att färglägga en graf kallas dess kromatiska tal.
F: Vad är syftet med att färglägga grafer?
S: Syftet med graffärgning är att hitta lösningar på problem inom grafteori som involverar färgning eller märkning av topparna i en graf enligt vissa villkor.
F: Varför är graffärgning viktigt?
S: Graffärgning är viktigt inom en mängd olika områden, inklusive datavetenskap, fysik och samhällsvetenskap, och kan användas för att modellera verkliga problem som schemaläggning, resursallokering och nätverksoptimering.
Sök