Grafteori | ett område av matematik om grafer
Grafteori är ett område inom matematiken som handlar om grafer. En graf är en abstrakt representation av: ett antal punkter som är förbundna med linjer. Varje punkt brukar kallas en hörn (fler än en kallas hörn), och linjerna kallas kanter. Grafer är ett verktyg för att modellera relationer. De används för att hitta svar på ett antal problem.
Några av dessa frågor är:
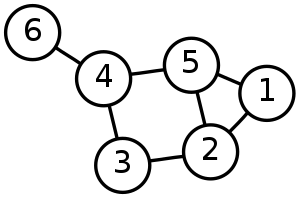
En oledd graf.
Olika typer av grafer
- Grafteorin har många aspekter. Grafer kan vara riktade eller oriktade. Ett exempel på en riktad graf är vägsystemet i en stad. Vissa gator i staden är enkelriktade gator. Det innebär att det på dessa delar bara finns en riktning att följa.
- Grafer kan viktas. Ett exempel är ett vägnät med avstånd eller vägtullar (för vägar).
- Noderna (cirklarna i schemat) i ett diagram kallas hörn. De linjer som förbinder noderna kallas kanter. Det kan inte finnas någon linje mellan två noder, det kan finnas en linje eller flera linjer.
- Inom grafteorin används ofta trädstrukturer som representerar hierarkiska strukturer. Ett träd är en riktad eller oriktad graf där det inte finns någon cykel, dvs. inget sätt att gå från en punkt (t.ex. en stad) till samma punkt med hjälp av varje kant som man bara använder en gång (man går bara en gång på varje väg som man tar).
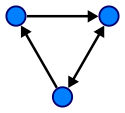
En riktad graf.
Historia
 →
→ →
→ 
En visualisering av Königbergs sju broar. Leonhard Euler löste detta problem 1736, vilket ledde till utvecklingen av topologi och modern grafteori.
En graf är en abstrakt datastruktur. Den innehåller noder som vanligtvis är relaterade till varandra. En nod är ett dataset, vanligtvis i form av ordnade par. Noder är antingen anslutna eller inte anslutna till en annan nod. Relationen mellan noder definieras vanligtvis som en kant. Grafer är användbara för sin förmåga att associera noder med andra noder. Det finns ett fåtal representationer av grafer i praktiken.
Leonhard Euler bodde i en stad som heter Königsberg. (Namnet ändrades till Kaliningrad 1946). Staden ligger vid floden Pregel. Det finns en ö i floden. Det finns några broar över floden. Euler ville gå runt och använda varje bro en gång. Han frågade om han kunde göra detta. År 1736 publicerade han en vetenskaplig artikel där han visade att detta inte var möjligt. Idag är detta problem känt som Königsbergs sju broar. Artikeln ses som den första artikeln i grafteorins historia.
Denna artikel, liksom Vandermondes artikel om riddarproblemet, fortsatte den analys av situs som Leibniz påbörjat. Eulers formel var om antalet kanter, hörn och ytor i en konvex polyeder studerades och generaliserades av Cauchy och L'Huillier och ligger till grund för topologin.
Fusionen av idéer från matematiken med idéer från kemin ligger till grund för en del av grafteorins standardterminologi. Termen "graf" introducerades av Sylvester i en artikel som publicerades 1878 i Nature.
Ett av de mest kända och produktiva problemen inom grafteorin är fyrfärgsproblemet: "Är det sant att alla kartor som ritas i planet kan ha sina regioner färgade med fyra färger, på ett sådant sätt att två regioner som har en gemensam gräns har olika färger?"
.png)
Samma problem, men med hjälp av en graf
.png)
Problemet med Königsbergbron, på en stadskarta
Grafteori i perspektiv
Grafteori är en viktig del av matematiken och datavetenskapen. För många av dessa problem finns det exakta lösningar. Många gånger är de dock mycket svåra att beräkna. Därför används ofta approximationer. Det finns två typer av sådana approximationer, Monte-Carlo-algoritmer och Las-Vegas-algoritmer.
Relaterade sidor
Frågor och svar
F: Vad är grafteori?
S: Grafteori är ett område inom matematiken där man studerar grafer, som är abstrakta representationer av punkter som är förbundna med linjer.
F: Vad kallas punkterna i en graf?
S: Punkterna i en graf brukar kallas hörnpunkter.
F: Vad representerar linjerna mellan hörnen?
S: Linjerna mellan hörnpunkterna representerar relationer eller förbindelser mellan dem.
F: Hur kan grafer användas?
S: Grafer kan användas för att modellera relationer och hitta svar på olika problem.
F: Vilken typ av frågor kan grafer hjälpa till att besvara?
S: Grafer kan hjälpa till att besvara frågor som rör nätverksanalys, optimering och schemaläggning.
F: Finns det olika typer av grafer?
S: Ja, det finns olika typer av grafer, t.ex. riktade och oriktade grafer, viktade och oviktade grafer, kompletta och ofullständiga grafer osv.
F: Finns det någon programvara för att arbeta med grafteori?
S: Ja, det finns programvara för att arbeta med grafteori, t.ex. Gephi och NetworkX.
Sök