Schemateoremet — John Hollands grundsats för genetiska algoritmer

Upptäck Schemateoremet: John Hollands grundsats om hur korta, högpresterande scheman i genetiska algoritmer växer exponentiellt—teori, kritik och koppling till Price‑ekvationen.

Författare: Leandro Alegsa

29-12-2025 23:40

Hollands schematsats, ofta kallad den grundläggande satsen för genetiska algoritmer, är en analytisk uppskattning som fångar en viktig mekanism bakom hur genetiska algoritmer arbetar. Schemateoremet säger i informella termer att korta, lågordnade scheman (mönster) som har högre fitness än populationsgenomsnittet tenderar att öka i frekvens i efterföljande generationer. Satsen föreslogs av John Holland på 1970‑talet och användes tidigt för att förklara varför genetiska algoritmer ofta hittar bra lösningar. Senare analyser har nyanserat den ursprungliga tolkningen; bland annat kan schemateoremet ses som ett specialfall av Price‑ekvationen när man använder schemaindikatorfunktionen som makroskopiskt mått, och flera studier har påpekat dess begränsningar i praktiska, stokastiska populationer.

Vad är ett schema?

Ett schema är ett mönster eller en mall som specificerar värden i vissa positioner i en bitsträng och lämnar andra positioner obestämda (vanligtvis betecknade med en jokertecken, t.ex. *). Ett enkelt exempel i binära strängar är schemat 1*0*, vilket beskriver alla strängar som har 1 i första positionen och 0 i tredje positionen, medan andra positioner kan vara antingen 0 eller 1. Formellt är scheman en specialform av cylindermängder och kan betraktas i ett topologiskt perspektiv som delar upp rymden av strängar i delmängder (delmängd), vilket också har samband med begrepp som topologiskt rum.

Formell version av schemateoremet

Schemateoremet uttrycks vanligen som en (nedre) ojämlikhet för det förväntade antalet kopior av ett schema H i nästa generation. I en vanlig formulering får man förväntat antal E[m(H,t+1)] minst

E[m(H,t+1)] ≥ m(H,t) · (f(H)/f_bar) · [1 − p_c · (δ(H)/(l−1))] · (1 − p_m)^{o(H)}

där

m(H,t) = antal individer som matchar schemat H vid generation t
f(H) = medelfitnessen bland individer som matchar H
f_bar = medelfitnessen i hela populationen
p_c = sannolikheten för korsning (crossover)
p_m = mutationssannolikheten per bit
δ(H) = definierande längd för H (avståndet mellan de yttre fasta positionerna)
o(H) = ordningen för H (antalet fasta positioner)
l = längden på kromosomerna (antal gener)

Formeln visar tre huvudmekanismer: selektion (f(H)/f_bar) som ökar frekvensen av bättre än medel‑schema, korsningsdisruption som är proportionell mot schemats definierande längd och mutationsdisruption som beror på schemats ordning.

Begrepp: ordning och definierande längd

Ordning o(H): antalet bestämda (icke‑jokertecken) positioner i schemat. Högre ordning innebär större sårbarhet för mutation (fler positioner kan mutera).
Definierande längd δ(H): avståndet mellan de första och sista bestämda positionerna i schemat. Ett schema med längre definierande längd löper större risk att brytas upp av crossover.

Byggstenshypotesen och tolkningar

Schemateoremet låg till grund för den så kallade byggstenshypotesen, som hävdar att genetiska algoritmer fungerar genom att kombinera korta, bra scheman ("byggstenar") till bättre och bättre lösningar över tiden. I denna tolkning samlas och rekombineras korta, lågordnade scheman selektivt för att bygga upp högkvalitativa individer.

Begränsningar och kritik

Schemateoremet är en nedre gräns (ojämlikhet), inte en exakt prediktion. Det ger en förväntad tendens, inte en deterministisk lag.
Det baseras vanligen på antaganden som proportionell selektion och förväntade värden; i ändliga populationer kan stokastiska effekter (genetisk drift) och urvalssampling ge stora avvikelser.
Kritiker har påpekat att schemateoremet inte räcker för att garantera att en GA finner globala optima, särskilt i problem med stark epistasis eller "deceptive" fitnesslandskap där kombinationer av byggstenar inte leder till bättre lösningar.
Analytiskt kan schemateoremet härledas inom en större ram, till exempel Price‑ekvationen; därför ses det numera ofta som en delkomponent i en mer allmän förklaringsmodell snarare än som en fristående förklaring.

Praktisk betydelse

Trots sina begränsningar har schemateoremet haft stor påverkan på hur man tänker kring representation och operatorer i evolutionära algoritmer. Det ger intuitiva riktlinjer:

Föredra representationer där bra egenskaper kan beskrivas av korta, lågordnade scheman.
Undvik onödigt höga mutationsnivåer som slår sönder ordningens bestämda positioner.
Anpassa crossover‑operatorer så att de inte rutinmässigt splittrar korta byggstenar (t.ex. använd punktkorsning eller positionella korsningsmetoder beroende på representation).

Moderna analyser av evolutionära algoritmer använder ofta kompletterande verktyg (stokastiska processer, informationsteori, dynamiska system med mera) för att få en mer komplett bild av beteendet i praktiska, ändliga populationer.

Exempel

Anta 8‑bitars kromosomer och schemat H = 1*0***1 (ordning o(H)=3, definierande längd δ(H)=6). Om m(H,t) = 10 och f(H)/f_bar = 1.2, p_c = 0.7 och p_m = 0.001 ger schemateoremet en uppskattning av hur många exemplar av H vi kan förvänta oss i nästa generation, med avräkning för både korsnings‑ och mutationsdisruption.

Sammanfattningsvis: Hollands schemateorem ger en användbar, intuitiv och formellt härledd förklaring till varför korta, lågordnade och övergenomsnittliga mönster ofta förstärks i genetiska algoritmer. Det är dock en del av ett större analytiskt ramverk och bör användas tillsammans med förståelse för dess antaganden och begränsningar i praktiska tillämpningar.

Beskrivning

Betrakta binära strängar med längden 6. Schemat 1*10*1 beskriver mängden av alla strängar med längden 6 med 1:or på positionerna 1, 3 och 6 och en 0 på position 4. * är en jokertecken-symbol, vilket innebär att positionerna 2 och 5 kan ha värdet 1 eller 0. Ordningen i ett schema o ( H ) {\displaystyle o(H)} $o(H)$ definieras som antalet fasta positioner i mallen, medan den definierande längden δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ är avståndet mellan den första och sista specifika positionen. Ordningen för 1*10*1 är 4 och dess definierande längd är 5. Ett schemas lämplighet är den genomsnittliga lämpligheten hos alla strängar som matchar schemat. En strängs lämplighet är ett mått på värdet av den kodade problemlösningen, som beräknas av en problemspecifik utvärderingsfunktion. Med hjälp av de etablerade metoderna och de genetiska operatörerna för genetiska algoritmer, säger schemateoremet att korta, lågt ordnade scheman med högre genomsnittlig lämplighet ökar exponentiellt i successiva generationer. Uttryckt som en ekvation:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Här är m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ antalet strängar som tillhör schema H {\displaystyle H} $H$ vid generation t {\displaystyle t}. $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ är den observerade genomsnittliga lämpligheten för schema H {\displaystyle H} $H$ och a t {\displaystyle a_{t}} $a_{t}$ är den observerade genomsnittliga lämpligheten vid generation t {\displaystyle t} $t$ . Sannolikheten för störning p {\displaystyle p} $p$ är sannolikheten för att crossover eller mutation kommer att förstöra schemat H {\displaystyle H} $H$ . Den kan uttryckas som:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

där o ( H ) {\displaystyle o(H)} $o(H)$ är ordningen i schemat, l {\displaystyle l} $l$ är kodens längd, p m {\displaystyle p_{m}} $p_{m}$ är sannolikheten för mutation och p c {\displaystyle p_{c}} $p_{c}$ är sannolikheten för crossover. Ett schema med en kortare definierande längd δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ har alltså mindre sannolikhet att bli störd.
En ofta missförstådd punkt är varför schematsatsen är en ojämlikhet snarare än en jämlikhet. Svaret är i själva verket enkelt: teoremet försummar den lilla, men icke-noll, sannolikheten att en sträng som tillhör schemat H {\displaystyle H} $H$ kommer att skapas "från grunden" genom mutation av en enda sträng (eller rekombination av två strängar) som inte tillhörde H {\displaystyle H} $H$ i den föregående generationen.

Begränsning

Schematsatsen gäller under antagandet att en genetisk algoritm upprätthåller en oändligt stor population, men den överförs inte alltid till den (ändliga) praktiken: på grund av provtagningsfel i den ursprungliga populationen kan genetiska algoritmer konvergera mot scheman som inte har någon selektiv fördel. Detta händer särskilt vid multimodal optimering, där en funktion kan ha flera toppar: populationen kan driva till att föredra en av topparna och ignorera de andra.

Skälet till att schemateoremet inte kan förklara de genetiska algoritmernas styrka är att det gäller för alla probleminstanser och inte kan skilja mellan problem där genetiska algoritmer presterar dåligt och problem där genetiska algoritmer presterar bra.

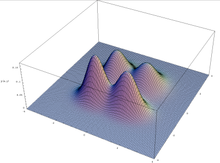
Plott av en multimodal funktion i två variabler.

Frågor och svar

F: Vad är Hollands schemateorem?

S: Hollands schemateorem är ett teorem om genetiska algoritmer som säger att individer med en fitness som är högre än genomsnittet är mer benägna att segra.

F: Vem föreslog Hollands schemateorem och när?

S: John Holland föreslog Hollands schemateorem på 1970-talet.

F: Vad är ett schema i samband med genetiska algoritmer?

S: I samband med genetiska algoritmer är ett schema en mall som identifierar en delmängd av strängar med likheter vid vissa strängpositioner.

F: Vad är tolkningen av Hollands schemateorem som användes som grund för förklaringar av kraften i genetiska algoritmer?

S: Tolkningen av Hollands schemateorem som användes som grund för förklaringar av genetiska algoritmers kraft är att individer med en fitness som är högre än genomsnittet är mer benägna att segra.

F: Vad har kritiken mot Hollands schemateorem visat att den är?

S: Kritik mot Hollands schemateorem har visat att det är ett specialfall av Price-ekvationen med schemats indikatorfunktion som makroskopisk mätning.

F: Vad är ett specialfall av cylinderuppsättningar?

S: Schemata är ett specialfall av cylindermängder.

F: Vilken typ av utrymme bildar schemata?

S: Schemata bildar ett topologiskt rum.

Sök