Young-Laplace ekvation
Inom fysiken är Young-Laplaceekvationen (/ləˈplɑːs/) en icke-linjär partiell differentialekvation som beskriver den kapillära tryckskillnaden över gränssnittet mellan två statiska vätskor, t.ex. vatten och luft. Denna skillnad beror på fenomenet ytspänning eller väggspänning. Väggspänning kan endast användas för mycket tunna väggar. Young-Laplace-ekvationen relaterar tryckskillnaden till ytans eller väggens form. Den är mycket viktig vid studier av statiska kapillära ytor.
Inom fysiologin är den känd som Laplaces lag. Den används för att beskriva trycket i ihåliga organ.
Ekvationen är uppkallad efter Thomas Young, som utvecklade den kvalitativa teorin om ytspänning 1805, och Pierre-Simon Laplace som fullbordade den matematiska beskrivningen året därpå. Den kallas ibland även Young-Laplace-Gauss-ekvationen: Carl Friedrich Gauss förenade Young och Laplaces arbete 1830. Gauss härledde både differentialekvationen och randvillkoren med hjälp av Johann Bernoullis principer för virtuellt arbete.
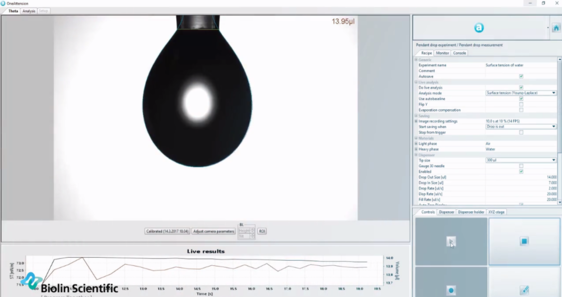
Optiska tensiometrar använder Young-Laplace-ekvationen för att automatiskt bestämma vätskans ytspänning utifrån dropparnas form.
Frågor och svar
Fråga: Vad är Young-Laplace-ekvationen?
S: Young-Laplace-ekvationen är en icke-linjär partiell differentialekvation som beskriver den kapillära tryckskillnaden över gränssnittet mellan två statiska vätskor, t.ex. vatten och luft.
F: Vad har den att göra med?
S: Den relaterar tryckskillnaden till ytans eller väggens form.
F: Vem utvecklade denna teori?
S: Teorin utvecklades av Thomas Young 1805 och Pierre-Simon Laplace slutförde den matematiska beskrivningen året därpå. Den förenhetligades senare av Carl Friedrich Gauss 1830.
F: Hur används den inom fysiologin?
S: Inom fysiologin är den känd som Laplaces lag och används för att beskriva trycket i ihåliga organ.
F: Vilket fenomen förklarar den?
S: Young-Laplace-ekvationen förklarar fenomenet ytspänning eller väggspänning.
F: Gäller väggspänning för tjocka väggar? S: Nej, väggspänning kan endast användas för mycket tunna väggar.
