Coulombs lag – definition, formel och exempel på elektrostatisk kraft

Coulombs lag: Lär dig definition, formel och praktiska exempel på elektrostatisk kraft — förstå hur två laddningar påverkar varandra och räkna ut kraften steg för steg.

Författare: Leandro Alegsa

24-12-2025 11:22

Coulombs lag är en funktion som utvecklades på 1780-talet av fysikern Charles-Augustin de Coulomb. Den förklarar hur stark kraften blir mellan två elektrostatiska laddningar. Elektrostatisk innebär att elektriska laddningar inte rör sig.

Definition

Coulombs lag beskriver den kraft som verkar mellan två punktladdningar i vila. Kraftens storlek är proportionell mot produkten av laddningarnas storlekar och omvänt proportionell mot kvadraten på avståndet mellan dem. Kraften är riktad längs linjen som förbinder laddningarna.

Formel (skalär och vektor)

Scalar form (storlek):

F = k · |q1 · q2| / r²

Här är

F kraftens storlek (Newton, N)
q1 och q2 laddningarna (Coulomb, C)
r avståndet mellan laddningarnas positioner (meter, m)
k proportionalitetskonstanten, i vakuum k = 1 / (4π·ε0) ≈ 8,98755179·10^9 N·m²/C² (vanligtvis avrundat till 9,0·10^9)

Vektorform (inklusive riktning):

F₁₂ = k · q1 · q2 / r² · r̂₁₂

där r̂₁₂ är enhetsvektorn som pekar från laddning 1 mot laddning 2. Tecknet hos produkten q1·q2 avgör riktningen: samma tecken ger repulsion (kraften pekar bortåt), motsatt tecken ger attraktion (kraften pekar inåt).

Konstant och medium

ε0 (permiviteten i vakuum) ≈ 8,854187817·10^−12 F/m.
I ett material (dielektrikum) ersätts ε0 med ε = εr·ε0, och kraften minskar med faktor 1/εr jämfört med vakuum.

Exempel: numerisk uträkning

Två punktladdningar q1 = +2,0 μC och q2 = −3,0 μC ligger 5,0 cm från varandra. Bestäm kraftens storlek och riktning.

q1 = 2,0·10^−6 C
q2 = −3,0·10^−6 C
r = 0,050 m
k ≈ 9,0·10^9 N·m²/C²

Beräkning:

F = k · |q1·q2| / r² = 9,0·10^9 · (2,0·10^−6 · 3,0·10^−6) / (0,050)² = 9,0·10^9 · 6,0·10^−12 / 0,0025 = 21,6 N

Eftersom laddningarna har motsatt tecken är kraften attraherande (de dras mot varandra) med storlek 21,6 N.

Elektriskt fält från Coulombs lag

Elektriskt fält definieras som kraft per enhetstestladdning:

E = k · q / r² · r̂

Det innebär att Coulombs lag omedelbart ger fältet från en punktladdning, och därefter kan kraften på en testladdning q_test fås som F = q_test · E.

Superpositionsprincipen

Om flera punktladdningar finns, kan den totala kraften på en laddning beräknas som vektorsumman av krafterna från varje enskild laddning. Coulombs lag är linjär i laddningarna och tillåter därför enkel summering:

F_total = Σ_i F_i = Σ_i k · q · q_i / r_i² · r̂_i

Egenskaper, begränsningar och tillämpningar

Coulombs lag gäller exakt för punktladdningar och för laddningsfördelningar som kan betraktas som punktlika (t.ex. sfäriskt symmetriska fördelningar utanför sfären).
På mycket små (atomära) avstånd krävs kvantmekaniska beskrivningar; Coulombs lag är då en klassisk approximation.
I material påverkas kraften av dielektriska egenskaper (relativ permittivitet εr).
Coulombs lag är ett fundamentalt verktyg inom elektrostatiska beräkningar och används i allt från enkel kraftanalys till beräkningar av fält i kondensatorer och kring ledningsfördelningar.

Relation till andra lagar

Formellt har Coulombs lag samma 1/r²‑beroende som Newtons gravitationslag, men tecknen och konstanterna skiljer — elektriska krafter kan vara attraktiva eller repulsiva beroende på laddningarnas tecken.
Coulombs lag är konsekvent med Gauss lag i elektrostatiken; Gauss lag ger ofta enklare sätt att beräkna fält för symmetriska laddningsfördelningar.

Historik i korthet

Charles-Augustin de Coulomb mätte krafter mellan laddade kroppar med en vridbalans under 1780‑talet och formulerade den lag som numera bär hans namn. Hans arbete gav en kvantitativ grund för klassisk elektrostatik.

Vanliga misstag att undvika

Glöm inte att använda radien r (inte diameter) i formeln.
Var noga med tecknet på laddningarna när du bestämmer riktningen (attraktion vs repulsion) — i vektorform hanteras detta automatiskt.
Räkna om enheter så att alla är i SI (C, m, N) innan du använder konstanten k.

Sammanfattningsvis ger Coulombs lag en enkel och kraftfull beskrivning av elektrostatisk kraft mellan punktladdningar: styrkan beror på laddningarnas storlekar, avståndet mellan dem och det omgivande mediets permittivitet.

Charles Augustin de Coulomb

Riktning

Låt oss tänka oss två elektriska laddningar i ett tomt utrymme. Om de två laddningarna är motsatta, till exempel + och -, kommer de att attrahera varandra. Och om två laddningar är lika, till exempel båda (+) eller båda (-), kommer de att trycka på varandra. Detta liknar hur magneter fungerar: N och S drar till sig varandra och N och N, S och S trycker på varandra.

Detta beror på att elektriska laddningar skapar ett elektriskt fält. Om två fält existerar i samma rum samtidigt, utövar de två fälten en kraft på varandra. Den kraft som de utövar på varandra kallas "Coulombs kraft" eller den elektrostatiska kraften. Coulombs lag förklarar hur stor kraften blir.

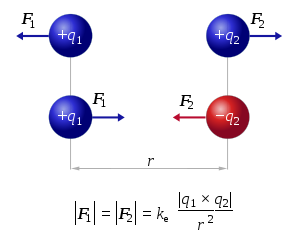
Den här bilden visar hur Coulombs kraft verkar; liknande laddningar trycker mot varandra och motsatta laddningar drar till sig varandra.

Skala

Coulombs lag förklarar skalan mellan två elektriska laddningar. Den elektrostatiska kraftens skala följer nedanstående funktion.

F = K c q 1 q 2 r 2 {\displaystyle F={K_{c}}{\frac {q_{1}q_{2}}{r^{2}}}} $F={K_{c}}{\frac {q_{1}q_{2}}{r^{2}}}$

Coulombs lag förklarar att kraftskalan F är relativ till förhållandet mellan q 1 , q 2 {\displaystyle q_{1},q_{2}}} $q_{1},q_{2}$ , 1 r 2 {\displaystyle {\frac {\frac {1}{r^{2}}}} ${\frac {1}{r^{2}}}$ .

q 1 {\displaystyle q_{1}} $q_{1}$ och q 2 {\displaystyle q_{2}} $q_{2}$ är skalorna för varje elektrisk laddning. r {\displaystyle r} är avståndet mellan de två elektriska laddningarna. Och K c {\displaystyle K_{c}} $K_{c}$ har ett visst värde. Det ändras inte i förhållande till q 1 {\displaystyle q_{1}}}. $q_{1}$ , q 2 {\displaystyle q_{2}}} $q_{2}$ eller r {\displaystyle r} . Medan K c {\displaystyle {K_{c}}} ${K_{c}}$ förblir konstant, kommer den elektrostatiska kraften också att bli större när multiplar av q 1 {\displaystyle q_{1}} $q_{1}$ och q 2 {\displaystyle q_{2}} $q_{2}$ blir större. När avståndet r {\displaystyle r} blir större blir den elektrostatiska kraften mindre i förhållande till 1 r 2 {\displaystyle {\frac {1}{r^{2}}}} ${\frac {1}{r^{2}}}$ . Den
exakta storleken på K c {\displaystyle K_{c}}} $K_{c}$ är k c = 8.987 551 787 × 10 9 {\displaystyle {\begin{aligned}k_{c}}&=8.987\ 551\ 787\times 10^{9}\\end{aligned}}} ${\begin{aligned}k_{c}&=8.987\ 551\ 787\ \times 10^{9}\\\end{aligned}}$ ≈ 9 × 10 9 {\displaystyle \approx 9\times 10^{9}}} $\approx 9\times 10^{9}$ N m² C⁻² (eller m F⁻¹ ). Denna konstant kallas Coulombs kraftkonstant eller den elektrostatiska kraftkonstanten.

Lagen om omvänt kvadrat

Förhållandet mellan tryck- eller dragkraften (F) och avståndet mellan partiklarna ( r {\displaystyle r} ) följer lagen om omvänd kvadrat. Den omvända kvadratlagen innebär att när avståndet r {\displaystyle r} blir större, blir kraften svagare i förhållandet 1 r 2 {\displaystyle {\frac {1}{r^{2}}}} ${\frac {1}{r^{2}}}$ . Gravitation, elektromagnetisk strålning och ljudstyrka följer också denna lag.

Relaterade sidor

Coulomb, SI-enheten för elektrisk laddning, uppkallad efter Charles-Augustin de Coulomb.
Invers kvadratlag, den fysikaliska lag som visar förhållandet mellan avstånd och intensitet.
Elektrostatisk
Magnetisk

Sök