Kurvanpassning: definition, metoder, interpolation och utjämning

Kurvanpassning är att konstruera en matematisk funktion som bäst passar en uppsättning datapunkter.

Kurvanpassning kan innebära antingen interpolering eller utjämning. Interpolation kräver en exakt anpassning till data. Vid utjämning konstrueras en "slät" funktion som passar data ungefärligt. Ett närliggande ämne är regressionsanalys, som är mer inriktad på frågor om statistisk slutsats, t.ex. hur stor osäkerhet som finns i en kurva som anpassas till data som observerats med slumpmässiga fel.

Anpassade kurvor kan användas för att visualisera data, för att gissa värden för en funktion när inga data finns tillgängliga och för att sammanfatta sambanden mellan två eller flera variabler. Extrapolering avser användning av en anpassad kurva utanför de observerade dataens område. Detta är behäftat med en viss grad av osäkerhet, eftersom det kan återspegla den metod som används för att konstruera kurvan lika mycket som den återspeglar de observerade uppgifterna.

Vanliga metoder för kurvanpassning

Minsta kvadraters metod (OLS) — Den vanligaste metoden för att hitta parametrar till en funktion genom att minimera summan av kvadrerade residualer: minimize Σ(yi − f(xi))^2. Lämplig när observationsfelen antas vara oberoende och ha konstant varians.
Viktad minsta kvadrater (WLS) — Används när observationsosäkerheten varierar; varje punkt vägs med omvänt proportionell vikt till variansen.
Polynom- och rationella funktioner — Enkel och ofta användbar, men höga polynomgrader kan ge oscillerande beteende (Runge-fenomen) och dålig extrapoleringsförmåga.
Splines och B-splines — Styckvis polynomiska funktioner som kopplas samman med villkor på kontinuitet; bra för att få en slät kurva utan att använda mycket höga polynomgrader.
Utjämningssplines och regularisering — Inför en straffterm (t.ex. integralen av kvadraten av andra derivatan) för att balansera passform och släthet. Ett sätt att undvika överanpassning.
LOESS / LOWESS — Lokal regressionsmetod som passar enkla modeller i ett rörligt fönster; bra för att fånga lokala mönster utan att anta en global funktionsform.
Kernel-smoothing och glidande medelvärde — Icke-parametriska metoder som bygger släthet genom lokala vikter.
Robusta metoder — M-estimatorer och andra tekniker som minskar påverkan från avvikande datapunkter (outliers).
Bayesianska och probabilistiska metoder — T.ex. Gaussiska processer som ger en fördelning över funktioner och inkluderar osäkerhet i prognoser.

Interpolation kontra utjämning

Interpolation tvingar kurvan att gå exakt genom alla datapunkter. Metoder är t.ex. polynominterpolation och styckvis interpolation med splines. Interpolering är lämpligt när mätdata anses exakta eller när man behöver återfinna funktionens värde mellan kända punkter.

Utjämning (smoothing) låter kurvan approximera datapunkterna utan att nödvändigtvis passera genom dem. Detta är användbart när data innehåller brus eller mätfel. Valet av utjämningsstyrka (smoothing parameter) påverkar bias–varians-avvägningen: för stark utjämning ger hög bias (undanförpassning), för svag utjämning ger hög varians (överanpassning).

Modellval, regularisering och överanpassning

Överanpassning uppstår när modellen fångar slumpmässigt brus i stället för underliggande struktur. Tecken är mycket låg felkvadrat på träningsdata men dålig förutsägelse på ny data.
Regularisering (t.ex. Ridge/Tikhonov, Lasso) lägger till en straffterm för modellens komplexitet och hjälper till att undvika överanpassning.
Cross-validation och kriterier som AIC, BIC eller justerat R^2 används för att välja modellens komplexitet och jämföra alternativa modeller.

Diagnostik och praktiska råd

Analysera residualerna: de bör vara slumpmässigt fördelade utan tydligt mönster. Avvikelser kan indikera felaktig funktionsform, heteroskedasticitet eller beroende i feltermerna.
Kontrollera inflytande och hävstång (leverage), t.ex. med Cook's distance, för att hitta punkter som oproportionerligt påverkar anpassningen.
Använd transformationer (log, kvadratrot) vid behov för att stabilisera varians eller linearisera samband.
Vid tidsserier, beakta autokorrelation i residualerna (Durbin–Watson-test) och använd lämpliga modeller eller korrigeringar.
Använd bootstrap eller bayesianska metoder för att uppskatta osäkerhet i anpassade kurvor när antaganden om fel inte håller.

Extrapolering och begränsningar

Extrapolering utanför det observerade område innebär ofta betydligt större osäkerhet än interpolation. Kurvans beteende utanför dataintervallet beror i hög grad på val av modellform; linjära modeller kan underskatta krökning, och högre ordningens polynom kan ge orealistiska svängningar. Var försiktig och kvantifiera osäkerheten om extrapolering ska användas i beslut eller prognoser.

Programvara och implementation

Det finns många verktyg för kurvanpassning: statistiska paket (R, Python med bibliotek som numpy, scipy, statsmodels, scikit-learn), matematikprogram (MATLAB) och specialiserade bibliotek för interpolation och splines. Val av verktyg beror på metoden (parametrisk, icke-parametrisk, bayesiansk) och praktiska krav på prestanda och tolkbarhet.

Sammanfattningsvis är kurvanpassning ett mångsidigt verktyg för att beskriva, visualisera och förutsäga samband i data. Rätt metodval, modellkontroll och förståelse för osäkerheter är centrala för att få tillförlitliga resultat.

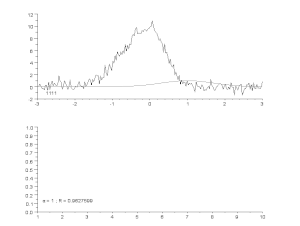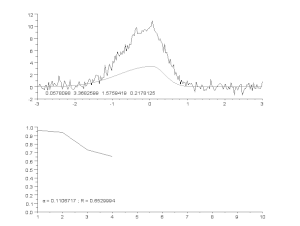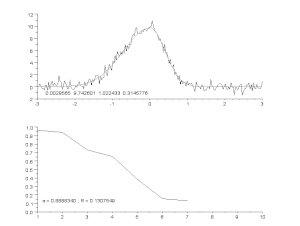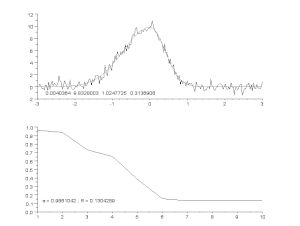
Anpassning av en bullrig kurva med en asymmetrisk toppmodell, med en iterativ process (Gauss-Newton-algoritm med variabel dämpningsfaktor α). Överst: rådata och modell. Nederst: utveckling av den normaliserade summan av felens kvadrater.

Frågor och svar

Fråga: Vad är kurvanpassning?

S: Kurvanpassning är processen att skapa en matematisk funktion som bäst passar en uppsättning datapunkter.

F: Vilka är de två typerna av kurvanpassning?

S: De två typerna av kurvanpassning är interpolering och utjämning.

F: Vad är interpolering?

S: Interpolation är en typ av kurvanpassning som kräver en exakt anpassning till data.

F: Vad är utjämning?

Svar: Utjämning är en typ av kurvanpassning där man konstruerar en "slät" funktion som passar data ungefärligt.

F: Vad är regressionsanalys?

Svar: Regressionsanalys är ett relaterat ämne som fokuserar på frågor om statistisk inferens, t.ex. hur stor osäkerhet som finns i en kurva som anpassas till data som observerats med slumpmässiga fel.

F: Vilka är några användningsområden för anpassade kurvor?

S: Anpassade kurvor kan användas för att hjälpa till att visualisera data, gissa värden för en funktion när inga data finns tillgängliga och sammanfatta samband mellan två eller flera variabler.

F: Vad är extrapolering?

S: Extrapolering är användningen av en anpassad kurva utanför de observerade dataens intervall. Detta är dock behäftat med en viss grad av osäkerhet eftersom det kan återspegla den metod som använts för att konstruera kurvan lika mycket som den återspeglar de observerade uppgifterna.