Vad är en funktion? Definition, domän och exempel i matematik

Lär dig vad en funktion är: tydlig definition, domän och praktiska exempel i matematik — förklarat steg för steg för elever och lärare.

Författare: Leandro Alegsa

07-12-2025 18:45

Inom matematiken är en funktion ett matematiskt objekt som för varje indata tilldelar ett entydigt utdata. Indatan kan vara ett tal, en vektor eller vilket element som helst i en mängd.

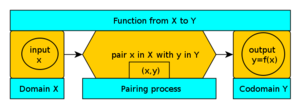
Man kan tänka på en funktion som en maskin som tar emot ett värde x och returnerar ett värde y. Mängden av alla tillåtna indata kallas domänen, och mängden som innehåller alla möjliga utdata kallas kodomänen. En funktion betecknas ofta med kursiva bokstäver, t.ex. f {\displaystyle f}, g {\displaystyle g} , h {\displaystyle h} $h$ .

Om detta sker säger vi att y är en funktion av x och skriver y = f ( x ) {\displaystyle y=f(x)} $y=f(x)$ . Här är f {\displaystyle f} namnet på funktionen, och man skriver f : X → Y {\displaystyle f:X\to Y} (funktion från X till Y) för att representera funktionens tre delar: domänen (X), kodomänen (Y) och avbildningen (pilen).

Ett enkelt exempel på en funktion är f ( x ) = x + 1 {\displaystyle f(x)=x+1} $f(x)=x+1$ . Om man t.ex. anger ett naturligt tal x {\displaystyle x} som indata får man ut ett annat naturligt tal y {\displaystyle y} som är x + 1 {\displaystyle x+1} $x+1$ . Om man till exempel ger 3 som indata till f {\displaystyle f} får man 4 som utdata.

En funktion behöver inte uttryckas som en enkel ekvation — huvudidén är att varje indata kopplas till exakt ett utdata, även om avbildningen kan vara mycket komplicerad eller byggd av flera steg.

Domän, kodomän och värdemängd

Domän: mängden av alla giltiga indata. Exempel: för f(x)=1/x är domänen alla reella tal utom 0.
Kodomän (målmängd): den mängd vi säger att funktionen avbildar till—vanligtvis en övergripande mängd som utdata hör till.
Värdemängd (bild eller "range"): den faktiska mängd av utdata som funktionen antar. Viktigt: värdemängden är en delmängd av kodomänen och behöver inte vara lika stor som kodomänen. Exempel: för f(x)=x^2 med f: R→R är värdemängden [0, ∞), medan kodomänen R innehåller även negativa tal som inte är bilder av något x.

Formella definitioner och representation

Formellt kan en funktion f från en mängd X till en mängd Y beskrivas som en mängd av ordnade par (x,y) med x∈X och y∈Y där varje x i X förekommer i exakt ett par. Man skriver f: X → Y och för varje x i X finns ett unikt y = f(x) i Y. Detta gör tydligt vad som krävs: entydighet (ett x får inte ge två olika y).

Vanliga egenskaper

Injektiv (en-till-en): olika indata ger olika utdata. Formellt: om f(x1)=f(x2) så är x1=x2.
Surjektiv (på): värdemängden är hela kodomänen, det vill säga varje element i kodomänen är bild av minst ett element i domänen.
Bijektiv: både injektiv och surjektiv. En bijektion har en invers funktion f^{-1} som går åt andra hållet.

Graf, visualisering och test

För reella funktioner f: R→R visualiseras ofta funktionen som en graf i ett koordinatsystem {(x,f(x))}. Ett praktiskt test: den vertikala linjetesten — om en vertikal linje skär grafen i mer än en punkt, så är relationen inte en funktion (eftersom ett x skulle ge flera y).

Sammansättning och invers

Man kan kombinera funktioner genom sammansättning: (f∘g)(x)=f(g(x)). Om f är bijektiv finns en invers f^{-1} med f^{-1}(f(x))=x för alla x i domänen.

Exempel

f(x)=x+1 med f: N → N. Här är domänen och kodomänen de naturliga talen, och värdemängden är också N.
g(x)=1/x med g: R\{0} → R\{0}. Domänen utesluter 0 eftersom 1/0 inte är definierat.
h(x)=x^2 med h: R → R. Domänen är alla reella tal, kodomänen kan anges som R, men värdemängden är [0, ∞).
En bitvis funktion, t.ex. f(x)= { x^2 för x≤0, 2x+1 för x>0 }, där regel för indata beror på var x ligger.
Funktioner kan också ha vektorer som värden eller argument, t.ex. F: R^2 → R där F(x,y)=x^2+y^2.

Funktioner i mer abstrakta sammanhang

I mer avancerad matematik används funktioner mellan godtyckliga mängder (inte bara tal). Funktioner är centrala i många teorier — från analys och algebra till sannolikhet och topologi — och kan beskrivas algebraiskt, geometriskt eller som algoritmer.

Sammanfattning: En funktion är en regel som tilldelar varje element i en domän ett entydigt element i en kodomän. Viktiga begrepp att skilja på är domän, kodomän och värdemängd, samt egenskaper som injektivitet, surjektivitet och möjligheten att bilda invers eller komponera funktioner.

Metaforer

Tabeller

In- och utdata kan placeras i en tabell som bilden; detta är enkelt om det inte finns för mycket data.

Diagram

I bilden kan man se att både 2 och 3 har kopplats ihop med c. Detta är inte tillåtet i den andra riktningen, eftersom 2 inte kan ge ut c och d samtidigt (varje ingång kan bara ha en utgång). Alla f ( x ) {\displaystyle f(x)} f(x) (c och d i bilden) brukar kallas för bildmängden av f {\displaystyle f} , och bildmängden kan vara hela kodomänen eller en av dess delmängder. Man kan säga att bildmängden för en delmängd A av domänen är f(A). Om ingångarna och utgångarna har en ordning är det lätt att plotta dem på en graf:

På så sätt kommer bilden till bilden av mängden A.

Historia

På 1690-talet använde Gottfried Leibniz och Johann Bernoulli ordet "funktion" i bokstäver mellan sig. Det moderna begreppet började alltså samtidigt med kalkylen.

År 1748 gav Leonhard Euler följande definition av funktion:

"En funktion av en variabel storhet är ett analytiskt uttryck som på något sätt är sammansatt av den variabla storheten och tal eller konstanta storheter."

och sedan år 1755:

"Om vissa storheter är så beroende av andra storheter att de förstnämnda förändras om de sistnämnda förändras, kallas de förstnämnda storheterna för funktioner av de sistnämnda. Denna definition gäller ganska brett och omfattar alla sätt på vilka en kvantitet kan bestämmas av andra. Om därför x betecknar en variabel storhet, så kallas alla storheter som på något sätt beror på x eller bestäms av den för funktioner av x."

Vanligtvis är det Peter Dirichlet som har den första moderna definitionen av funktion (formulerad 1837). Den användes ofta i skolor fram till andra hälften av 1900-talet:

"y är en funktion av en variabel x, definierad i intervallet a < x < b, om det till varje värde av variabeln x i detta intervall finns ett bestämt värde av variabeln y. Det är också irrelevant på vilket sätt denna korrespondens upprättas."

År 1939 generaliserade Bourbaki Dirichlet-definitionen och gav en mängdteoretisk version av definitionen som en korrespondens mellan in- och utdata.

1970 gav Bourbaki slutligen den moderna definitionen som en trippel f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} , med F ⊂ X × Y , ( x , f ( x ) ) ∈ $F\subset X\times Y,(x,f(x))\in F$ (dvs. f : X → Y {\displaystyle f:X\till Y} och F = { ( x , f ( x ) ) ∣ $F=\{(x,f(x))\mid x\in X,f(x)\in Y\}$ ). $X$ kallas för $f:s$ domän, $Y$ för dess kodomän och $F$ för dess graf. Mängden av alla element av formen $f (x),$ där $x$ sträcker sig över elementen i domänen $X$ , kallas bilden av $f$ . Bilden av en funktion är en delmängd av dess koddomän och kanske inte sammanfaller med den.

Typer av funktioner

Elementära funktioner - De funktioner som vanligtvis studeras i skolan: bråk, kvadratrötter, sinus-, cosinus- och tangentfunktionen samt några andra funktioner.
Icke elementära funktioner - De flesta av dem använder operationer som vi inte lär oss i skolan (som + eller - eller potenser). Många integraler är till exempel inte elementära.
Inversa funktioner - Funktioner som upphäver en annan funktion. Till exempel: Om F(x) är inversen av f(x)=y, så är F(y)=x. Alla funktioner har inte inverser.
Särskilda funktioner: Funktioner som har namn. Dessa inkluderar trigonometriska funktioner som sinus, cosinus och tangent. Funktioner som f(x)=3x (tre gånger x) kallas inte specialfunktioner. Specialfunktioner kan vara elementära, icke-elementära eller inverser.

Relaterade sidor

Konstant funktion
Kontinuerlig funktion
Funktionens sammansättning
Särskilda funktioner

Gammafunktion
Matrisfunktion

Linjär funktion
Lucy Joan Slater - brittisk matematiker som studerade matematiska funktioner.
MATLAB, Wolfram Mathematica - programvara för att beräkna matematiska funktioner.
Relation (matematik)

Frågor och svar

F: Vad är en funktion i matematiken?

S: En funktion i matematik är ett objekt som producerar en utgång när det ges en ingång, vilket kan vara ett tal, en vektor eller något som kan existera inom en mängd saker.

F: Vilka är de två uppsättningar som är förknippade med funktioner?

S: Mängden med alla värden som x kan ha kallas domänen och den mängd som innehåller alla värden som y kan ha kallas kodomänen.

Fråga: Hur betecknas funktioner ofta?

S: Funktioner betecknas ofta med kursiva bokstäver, t.ex. f, g, h.

F: Hur representerar vi en funktion?

S: Vi representerar en funktion genom att skriva y = f(x), där f är funktionens namn och man skriver f : X → Y (funktion från X till Y) för att representera funktionens tre delar - domän (X), koddomän (Y) och parningsprocessen (pilen).

F: Kan du ge ett exempel på en funktion?

S: Ett exempel på en funktion är f(x) = x + 1. Man ger ett naturligt tal x som indata och får det naturliga talet y som är x + 1. Om man till exempel ger 3 som indata till f får man 4 som utdata.

Fråga: Måste varje funktion vara en ekvation?

S: Nej, alla funktioner behöver inte vara ekvationer. Huvudidén bakom funktioner är att ingångar och utgångar kopplas ihop på något sätt - även om det kan vara mycket komplicerat.

Sök