Uppsättning | en idé från matematiken

Vad ska man göra med uppsättningar?

Föreställ dig att uppsättningen är en väska.

Element av

I en väska kan man lägga olika saker. Senare kan en bra fråga vara om en viss sak finns i påsen. Matematikerna kallar detta element för. Något är ett element i en mängd om det finns i påsen. Symbolen som används för detta är ∈ {\displaystyle \in } :

a ∈ A {\displaystyle a\in {\mathit {A}}}} ,

vilket innebär att en {\displaystyle a} ingår i påsen A {\displaystyle {\mathit {A}}} eller att en {\displaystyle a} ingår i A {\displaystyle {\mathit {A}}} .

Till skillnad från en påse kan en uppsättning innehålla högst ett objekt av en viss typ. För en uppsättning frukter spelar det alltså ingen roll om det finns en apelsin eller 10 apelsiner.

Tom uppsättning

Precis som en väska kan en uppsättning också vara tom. En tom mängd är som en tom väska: den har ingenting i sig. Den "tomma mängden" kallas också för nollmängden och representeras av symbolen ∅ {\displaystyle \varnothing } .

Universum

Om vi betraktar till exempel vissa uppsättningar av amerikanska bilar, t.ex. en uppsättning av alla Fords och en uppsättning av alla Dodges, kanske vi också vill betrakta hela uppsättningen av amerikanska bilar. I detta fall skulle mängden av alla amerikanska bilar kallas ett universum.

Med andra ord är ett universum en samling av alla element som man vill ta hänsyn till i ett visst problem. Universumet benämns vanligen U {\displaystyle U} .

Jämförelse av uppsättningar

Två uppsättningar kan jämföras. Det är som att titta i två olika väskor. Om de innehåller samma saker är de lika stora. Det spelar ingen roll i vilken ordning dessa saker är.

Till exempel, om A = { S t a n f o r d , S t a n l e y } {\displaystyle {\mathit {A}}}=\{Stanford,Stanley\}} och B = { S t a n l e y , S t a n f o r d } {\displaystyle {\mathit {B}}=\{Stanley,Stanford\}} är uppsättningarna desamma.

Kardinaliteten hos en mängd

När matematiker talar om en mängd vill de ibland veta hur stor en mängd är (eller hur stor dess kardinalitet är). Det gör de genom att räkna hur många element som ingår i mängden (hur många föremål som finns i påsen). För ändliga mängder är kardinaliteten ett enkelt tal. Den tomma mängden har kardinaliteten 0. Mängden { a p p l e , o r a n g e } {\displaystyle \{apple,orange\}} har kardinaliteten 2.

Två mängder har samma kardinalitet om vi kan para ihop deras element - om vi kan sammanfoga två element, ett från varje mängd. Mängden { a p p l e , o r a n g e } {\displaystyle \{apple,orange\}}} och mängden { s u n , m o o n } {\displaystyle \{sun,moon\}} har samma kardinalitet. Vi kan t.ex. para ihop äpple med sol och apelsin med måne. Ordningen spelar ingen roll. Det är möjligt att para ihop alla element, och inget element lämnas utanför. Men mängden { d o g , c a t , b i r d } {\displaystyle \{dog,cat,bird\}} och mängden { 5 , 6 } {\displaystyle \{5,6\}} har olika kardinalitet. Om vi försöker para ihop dem, lämnar vi alltid bort ett djur.

Oändlig kardinalitet

Ibland är kardinaliteten inte ett nummer. Ibland har en mängd oändlig kardinalitet. Mängden av alla heltal är en mängd med oändlig kardinalitet. Vissa mängder med oändlig kardinalitet är större (har större kardinalitet) än andra. Det finns till exempel fler verkliga tal än naturliga tal, vilket innebär att vi inte kan para ihop mängden heltal och mängden verkliga tal, även om vi skulle arbeta i all evighet.

Räkneförmåga

Om man kan räkna elementen i en mängd kallas den en räknbar mängd. Räknebara mängder omfattar alla mängder med ett ändligt antal medlemmar. Räknebara mängder omfattar också vissa oändliga mängder, som de naturliga talen. Du kan räkna de naturliga talen med 1 , 2 , 3 ... {\displaystyle {1,2,3...}} . De naturliga talen har fått smeknamnet "de räknebara talen", eftersom det är dem vi vanligtvis använder för att räkna saker med.

En oräknelig mängd är en oändlig mängd som är omöjlig att räkna. Om vi försöker räkna elementen kommer vi alltid att hoppa över några. Det spelar ingen roll vilket steg vi tar. Mängden reella tal är en oräknelig mängd. Det finns många andra oräkneliga mängder, till och med ett så litet intervall som [ 0 , 1 ] {\displaystyle [0,1]} .[3]

Undergrupper

Om du tittar på mängden A = { a , b } {\displaystyle A=\{a,b\}} och mängden B = { a , b , c , d } {\displaystyle B=\{a,b,c,d\}} kan man se att alla element i den första mängden också finns i den andra mängden.
 Vi säger: Vi säger också: { a , b } {\displaystyle \{a,b\}} är en delmängd av { a , b , c , d } {\displaystyle \{a,b,c,d\}}
 Som en formel ser det ut så här:
{ a , b } ⊆ { a , b , c , d } {\displaystyle \{a,b\}\subseteq \{a,b,c,d\}}

När alla element i mängden A {\displaystyle A} också är element i mängden B {\displaystyle B} , kallar vi A {\displaystyle A} för en delmängd av B {\displaystyle B} :
A ⊆ B {\displaystyle A\subseteq B} .
Vanligtvis läses det "A {\displaystyle A} ingår i B {\displaystyle B} ."

Exempel: Varje Chevrolet är en amerikansk bil. Så mängden av alla Chevrolets ingår i mängden av alla amerikanska bilar.

Ange åtgärder

Det finns olika sätt att kombinera uppsättningar.

Korsningar

Skärningspunkten A ∩ B {\displaystyle A\cap B} mellan två uppsättningar A {\displaystyle A} och B {\displaystyle B} är en uppsättning som innehåller alla element som samtidigt finns både i uppsättning A {\displaystyle A} och i uppsättning B {\displaystyle B} .

Exempel: När A {\displaystyle A} är mängden av alla billiga bilar och B {\displaystyle B} är mängden av alla amerikanska bilar, så är A ∩ B {\displaystyle A\cap B} mängden av alla billiga amerikanska bilar.

Fackföreningar

Föreningen A ∪ B {\displaystyle A\cup B} av två uppsättningar A {\displaystyle A} och B {\displaystyle B} är en uppsättning som innehåller alla element som finns i uppsättning A {\displaystyle A} eller i uppsättning B {\displaystyle B} . Detta "eller" är en inkluderande disjunktion, så föreningen innehåller också de element som finns i uppsättning A {\displaystyle A} och i uppsättning B {\displaystyle B} . Det betyder förresten att skärningspunkten är en delmängd av föreningen: ( A ∩ B ) ⊆ ( A ∪ B ) {\displaystyle (A\cap B)\subseteq (A\cup B)} .

Exempel: När A {\displaystyle A} är mängden av alla billiga bilar och B {\displaystyle B} är mängden av alla amerikanska bilar, så är A ∪ B {\displaystyle A\cup B} mängden av alla bilar, utan alla dyra bilar som inte är från Amerika.

Kompletterar

Komplement kan betyda två olika saker:

• Komplementet till A {\displaystyle A} är universum U {\displaystyle U} utan alla element i A {\displaystyle A} :

A C = U ∖ A {\displaystyle A^{\rm {C}}=U\setminus A}
 Universum U {\displaystyle U} är mängden av alla saker du talar om.
Exempel: När U {\displaystyle U} är mängden av alla bilar, och A {\displaystyle A} är mängden av alla billiga bilar,
så är A {\displaystyle A}^C mängden av alla dyra bilar.

• Mängdskillnaden mellan A {\displaystyle A} och B {\displaystyle B} är mängden B {\displaystyle B} utan alla element i A {\displaystyle A} :

B ∖ A {\displaystyle B\setminus A}
 Det kallas också det relativa komplementet till A {\displaystyle A} i B {\displaystyle B} .
Exempel: När A {\displaystyle A} är mängden av alla billiga bilar och B {\displaystyle B} är mängden av alla amerikanska bilar, så är B ∖ A {\displaystyle B\setminus A} mängden av alla dyra amerikanska bilar.

Om du byter ut uppsättningarna i skillnaden blir resultatet annorlunda:
I exemplet med bilarna är skillnaden A ∖ B {\displaystyle A\setminus B} uppsättningen av alla billiga bilar som inte är tillverkade i Amerika.

 
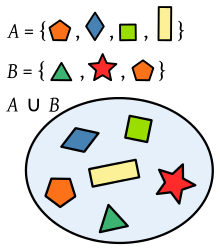
Union av två uppsättningar polygoner  


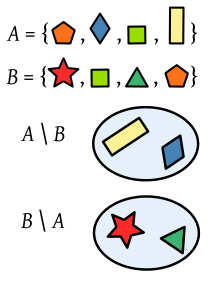
Skillnader mellan två uppsättningar polygoner  


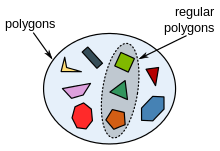
En delmängd av regelbundna polygoner  


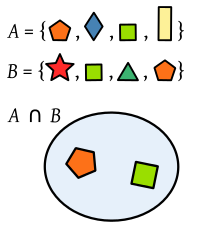
Skärning av två uppsättningar polygoner  

Notation

De flesta matematiker använder stora italienska bokstäver (vanligtvis romerska) för att skriva om mängder (t.ex. A {\displaystyle A} , B {\displaystyle B} , C {\displaystyle C} ). De saker som ses som element i uppsättningar skrivs vanligtvis med små bokstäver i romerska bokstäver.

Ett sätt att visa en mängd är att lista dess medlemmar, separerade med kommatecken och inskrivna i parenteser. Till exempel,

• X = { 1 , 2 , 3 } {\displaystyle X=\{{1,2,3\}}} är en mängd med medlemmarna 1, 2 och 3.

Ett annat sätt, som kallas set-builder-notationen, är att ange vad som är sant för medlemmarna i mängden, till exempel så här:

• {x | x är ett naturligt tal & x < 4}.

På talad engelska lyder detta: "mängden av alla x så att x är ett naturligt tal och x är mindre än fyra". Symbolen [ipe "|" betyder "så att" eller "så att".

Den tomma mängden skrivs på ett speciellt sätt: ∅ {\displaystyle \emptyset } , ∅ {\displaystyle \varnothing } eller { } {\displaystyle \{\}} .

När objektet a är medlem av mängden A {\displaystyle A} skrivs det som:

• a ∈ A.

På talad engelska lyder detta: "a är en medlem av A {\displaystyle A} ".

 

Venn-diagram

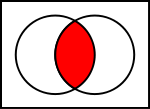
För att illustrera operationer på mängder använder matematiker Venn-diagram. Venndiagrammen använder cirklar för att visa enskilda mängder. Universum avbildas med en rektangel. Resultaten av operationer visas som färgade områden. I illustrationen av skärningsoperationen visar den vänstra cirkeln mängden A {\displaystyle A} och den högra cirkeln mängden B {\displaystyle B} .

 

 

Särskilda uppsättningar

Vissa uppsättningar är mycket viktiga för matematiken. De används mycket ofta. En av dessa är den tomma mängden. Många av dessa speciella mängder är skrivna med svart tavla fet stil, och dessa inkluderar:

• P {\displaystyle \mathbb {P} } , som betecknar mängden av alla primtal.
• N {\displaystyle \mathbb {N} } , som betecknar mängden av alla naturliga tal. Det vill säga, N {\displaystyle \mathbb {N} } = {1, 2, 3, ...}, eller ibland N {\displaystyle \mathbb {N} } = {0, 1, 2, 3, ...}.
• Z {\displaystyle \mathbb {Z} } , som betecknar mängden av alla heltal (positiva, negativa eller noll). Så Z {\displaystyle \mathbb {Z} } = {..., -2, -1, 0, 1, 2, ...}.
• Q {\displaystyle \mathbb {Q} } , som betecknar mängden av alla rationella tal (dvs. mängden av alla korrekta och okorrekta bråk). Q = { a b | a , b ∈ Z , b ≠ 0 } {\displaystyle \mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}\end{matrix}}}|a,b\in \mathbb {Z} ,b\neq 0\right\}}} , dvs. alla bråk a b {\displaystyle {\begin{matrix}{\frac {a}{b}}\end{matrix}}}} där a och b ingår i mängden av alla heltal och b inte är lika med 0. Till exempel 1 4 ∈ Q {\displaystyle {\begin{matrix}{\frac {1}{4}}}\end{matrix}}}\in \mathbb {Q} } och 11 6 ∈ Q {\displaystyle {\begin{matrix}{\frac {11}{6}}\end{matrix}}}\in \mathbb {Q} } . Alla heltal ingår i denna mängd eftersom varje heltal a kan uttryckas som bråket a 1 {\displaystyle {\begin{matrix}{\frac {a}{1}}}\end{matrix}}}} .
• R {\displaystyle \mathbb {R} } , som betecknar mängden av alla reella tal. Denna mängd omfattar alla rationella tal, tillsammans med alla irrationella tal (dvs. tal som inte kan skrivas om som bråk, t.ex. π , {\displaystyle \pi ,} e , {\displaystyle e,} och √2).
• C {\displaystyle \mathbb {C} } , som betecknar mängden av alla komplexa tal.

Var och en av dessa taluppsättningar har ett oändligt antal element, och P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C {\displaystyle \mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} } .

 

Paradoxer om mängder

Matematikern Bertrand Russell upptäckte att det finns problem med den informella definitionen av mängder. Han konstaterade detta i en paradox som kallas Russells paradox. En enklare version, som ligger närmare verkligheten, kallas Barberparadoxen.

Paradoxen med frisören

Det finns en liten stad någonstans. I den staden finns det en frisör. Alla män i staden gillar inte skägg, så antingen rakar de sig själva eller så går de till barberaren för att bli rakade av barberaren.

Vi kan därför göra ett uttalande om frisören själv: Barberaren rakar alla män som inte rakar sig själva. Han rakar bara dessa män (eftersom de andra rakar sig själva och inte behöver en barberare för att raka sig).

Detta väcker naturligtvis frågan: Vad gör frisören varje morgon för att se rakad ut? Detta är paradoxen.

Om barberaren rakar sig själv kan han inte vara barberare, eftersom en barberare inte rakar sig själv. Om han inte rakar sig själv, hör han till kategorin av dem som inte rakar sig själva och kan därför inte vara barberare.

 

Relaterade sidor

• Cantor-uppsättning
• Gruppteori
• Öppen uppsättning
• Relation
• Mängdteori