Ellips – definition, egenskaper och ekvationer
Lär dig ellipsens definition, egenskaper och viktiga ekvationer – från fokus och axlar till standardform och tillämpningar i planetbanor och geometri.
En ellips är en sluten kurva i planet som liknar en oval eller en tillplattad cirkel. I geometrin uppstår en ellips som en plan kurva som bildas när en kon skärs av ett snittplan så att skärningen blir en sluten kurva.
Egenskaper
En ellips kan också definieras som platsen för alla punkter i planet vars avstånd till två fasta punkter (de två fokus,) har en konstant summa. De två fasta punkterna kallas fokus (plural: fokus eller foci). En cirkel är ett specialfall av ellips där de två fokuserna sammanfaller i ett enda centrum.
De viktigaste geometriska elementen hos en ellips är:
- Centrum (h,k) – mittpunkten mellan de två fokuspunkterna.
- Semi-axlar a och b – avstånden från centrum till ellipsens ändpunkter längs huvudaxlarna. Den längre av dessa, kallad semi-stora axeln, betecknas ofta a, och den kortare semi-lilla axeln betecknas b.
- Huvudaxel – linjen genom centrum och båda ändpunkterna för den långa axeln (längd 2a).
- Sidaxel – linjen genom centrum och båda ändpunkterna för den korta axeln (längd 2b).
- Fokuser – två punkter på huvudaxeln på avstånd c från centrum, där c uppfyller c^2 = a^2 − b^2 (när a ≥ b).
- Eccentricitet e = c/a, ett tal mellan 0 och 1 som beskriver ellipsens "utsträckning" (e = 0 för en cirkel).
Ekvationer och parametrisering
För en ellips vars axlar är parallella med koordinataxlarna och med centrum i (h,k) gäller i standardform:
( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}}{a^{2}}}}+{\frac {(y-k)^{2}}}{b^{2}}}}=1}
I klar text: ((x − h)^2)/(a^2) + ((y − k)^2)/(b^2) = 1. Här är a semi-stora axeln och b semi-lilla axeln. Om a > b är ellipsens huvudaxel horisontell; om b > a är huvudaxeln vertikal (i så fall används ofta formen ((x − h)^2)/(b^2) + ((y − k)^2)/(a^2) = 1 efter omdefiniering så att a alltid betecknar semi-stora axeln).
Relationen mellan a, b och c (avståndet från centrum till varje fokus) är
c^2 = a^2 − b^2.
Parametriskt kan ellipsen skrivas som
x(t) = h + a cos t, y(t) = k + b sin t, för t i [0, 2π).
Allmän andragradsekvation för en konisk snitt (möjlig rotat ellips) är
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0, där villkoret för att kurvan ska vara en ellips (och inte hyperbel eller parabel) är B^2 − 4AC < 0 (för reella koefficienter och att den beskriver en sluten kurva).
Yta, omkrets och andra formler
Arean för en ellips är enkel:
Area = πab.
Omkretsen (perimetern) saknar enkel sluten form i elementär funktioner, men det finns noggranna approximationer. En välkänd approximation av Ramanujan är:
P ≈ π [3(a + b) − sqrt((3a + b)(a + 3b))].
Det finns också mer precisa serier och numeriska metoder för att beräkna omkretsen.
Tillämpningar och exempel
En praktisk konstruktion av en ellips är "två-nål-metoden": sätt två nålar i ett papper i positions för fokuspunkterna, loopa ett snöre runt dem och håll en penna spänd i snöret; genom att dra pennan runt så att snöret är spänt ritas en ellips — summan av avstånden till nålarna är konstant.
I astronomin beskriver Keplers första lag att planeternas banor runt solen är ellipser med solen i ett av fokusen. Det är ett viktigt exempel på hur ellipser uppträder i naturen.
Ytterligare anmärkningar
- En cirkel är ett specialfall där a = b (alltså e = 0).
- En horisontellt orienterad ellips har fokus på (h ± c, k); en vertikalt orienterad ellips har fokus på (h, k ± c).
- Rotera en ellips kring sitt centrum ändrar termerna i den kvadratiska formen (B ≠ 0) och kräver diagonaliseringsprocedurer eller koordinatrotation för att återgå till standardform.
Om du vill ha konkreta exempel (med numeriska värden på a, b, c), grafiska skisser eller härledningar av formlerna, kan jag lägga till det också.
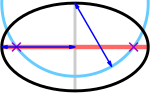
Brännpunkterna (lila kryss) ligger i skärningspunkterna mellan huvudaxeln (röd) och en cirkel (cyan) med en radie som är lika stor som den halva huvudaxeln (blå), centrerad på en ände av den lilla axeln (grå).

En ellips som erhålls som skärningspunkten mellan en kon och ett plan.
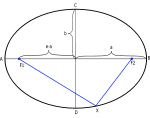
En ellips och dess egenskaper.
Frågor och svar
F: Vad är en ellips?
S: En ellips är en form som ser ut som en oval eller en tillplattad cirkel. Inom geometrin är det en plan kurva som uppstår när en kon skärs av ett plan på ett sätt som ger en sluten kurva.
F: Hur skapar man en ellips?
S: En ellips kan skapas genom att sätta två stift i kartong och sedan slinga ett snöre runt dessa två stift och sätta en penna i slingan och dra så långt som möjligt utan att bryta snöret i alla riktningar.
F: Vad är cirklar specialfall av?
S: Cirklar är specialfall av ellipser, som skapas när snittplanet är vinkelrätt mot konens axel.
Fråga: Hur många brännpunkter har en ellips?
S: En ellips har två brännpunkter.
Fråga: Vilken ekvation beskriver en ellips?
S: Ekvationen för en ellips är (x - h)²/a² + (y - k)²/b² = 1 där h och k representerar ellipsens centrum och 2a representerar längden från varje ände av den längre magra sidan, medan 2b representerar längden mellan varje ände av den kortare sidan. C representerar längden mellan dess brännpunkt och centrum, så att A²-B²=C².
Fråga: Var ser vi exempel på elliptiska banor?
S: Elliptiska banor kan ses hos planeter med solen i en av fokuspunkterna.
Sök