Cirkel – definition och formler: radie, diameter, omkrets & area
Lär dig allt om cirkeln: definition, radie, diameter, omkrets och area med tydliga formler, exempel och förklaringar — perfekt för studier och snabb repetition.
En cirkel är en rund, tvådimensionell form. Alla punkter på cirkelns kant är på samma avstånd från centrum.
En cirkels radie är en linje från cirkelns centrum till en punkt på sidan. Matematiker använder bokstaven 

Diametern (som betyder "hela vägen över") i en cirkel är en rak linje som går från en sida till den motsatta sidan och rakt igenom cirkelns centrum. Matematiker använder bokstaven 


En cirkels omkrets (som betyder "hela vägen runt") är den linje som går runt cirkelns centrum. Matematiker använder bokstaven 
Talet π (skrivet som den grekiska bokstaven pi) är ett mycket användbart tal. Det är omkretsens längd dividerat med diameterns längd ( 





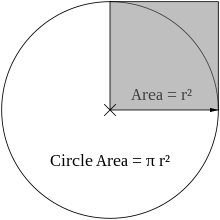
Området, 





Viktiga formler — översikt
- Diameter: d = 2r (diametern är dubbla radien).
- Omkrets (längden runt cirkeln): C = 2πr = πd.
- Area (ytan inuti cirkeln): A = πr² = π(d/2)² = πd²/4.
Enheter och tolkning
Om radien anges i meter (m) blir omkretsen i meter och arean i kvadratmeter (m²). Om radien anges i centimeter blir arean i cm², osv. Tänk på att area alltid får kvadratenhet.
Bågar, sektorer och strängar
- Båglängd: Längden av en båge med centralvinkel θ (i radianer) är s = rθ. För vinklar i grader konverterar du först: θ(rad) = θ(°)·π/180.
- Sektor (tårtbit): Arean av en sektor med vinkel θ (i radianer) är A_sektor = ½ r² θ.
- Sträng (chord): Längden på en sträng som skär av en vinkel θ i centrum (i radianer) är c = 2r·sin(θ/2).
- Cirkelsegment: Arean av ett segment (delen av cirkeln avgränsad av en sträng och motsvarande båge) med centralvinkel θ är A_segment = ½ r²(θ − sin θ), där θ är i radianer.
Exempel
Anta r = 3 cm. Med π ≈ 3,1416 får vi:
- Omkrets: C = 2πr ≈ 2·3,1416·3 ≈ 18,8496 cm.
- Area: A = πr² ≈ 3,1416·3² ≈ 28,2744 cm².
Mer om π
Talets π är irrationellt (kan inte skrivas som ett ändligt eller upprepande bråk) och till och med transcendental (det är inte roten till något icke-noll polynom med heltalskoefficienter). Det betyder att decimalerna aldrig upprepar sig och fortsätter i all oändlighet. För praktiska beräkningar används ofta avrundningar som 3,14 eller 3,1416, eller när högre noggrannhet behövs används rationella approximationer som 22/7 eller 355/113.
Användning och tillämpningar
Cirkelformer och formler för omkrets och area används i många praktiska sammanhang: mätning av hjulspår, beräkning av materialåtgång för runda ytor, konstruktioner med bågar, planering av rundade parkytor, samt inom fysik och teknik (t.ex. vågor, rotation och områden för tvärsnitt). Formlerna för båglängd och sektor är viktiga när man arbetar med vinklar, t ex vid konstruktion av cirkulära bågar och vid beräkning av områden för utskurna delar.
Tips
- Skriv om formler i termer av den storhet du känner (t.ex. om du känner diametern d, använd C = πd och A = πd²/4).
- Kontrollera enheterna – area = längd².
- Använd radianer i formler för båglängd, sektorarea och stränglängd om du använder de enkla uttrycken ovan; konvertera grader till radianer vid behov.

En cirkel
Beräkning av π






Även om denna serie är lätt att skriva och beräkna är det inte lätt att se varför den är lika med 





Genom att hitta en uppsättning punkter inuti cirkeln kan cirkelns area 




Beräkning av en cirkels area, omkrets, diameter och radie
Område
Med hjälp av dess radie:
Genom att använda dess diameter:
Med hjälp av dess omkrets:
Omkrets
Genom att använda dess diameter:
Med hjälp av dess radie:
Användning av sitt område:
Diameter
Med hjälp av dess radie:
Med hjälp av dess omkrets:
Med hjälp av dess area:
Radius
Med hjälp av dess diameter:
Med hjälp av dess omkrets:
Med hjälp av dess area:
Relaterade sidor
- Halvcirkel
- Sfär
- Att göra cirkeln fyrkantig
- Pi
- Pi (bokstav)
- Tau
Frågor och svar
F: Vad är en cirkel?
S: En cirkel är en rund, tvådimensionell form. Alla punkter på cirkelns kant befinner sig på samma avstånd från centrum.
F: Vad använder matematiker för att representera längden på en cirkels radie?
S: Matematiker använder bokstaven r för längden på en cirkels radie.
F: Vad skrivs som O i cirklar?
S: En cirkels centrum skrivs ofta med O.
F: Hur lång är diametern på en cirkel?
S: En cirkels diameter (som betyder "hela vägen över") är en rät linje som går från en sida till den motsatta och rakt genom cirkelns centrum. Den är lika med två gånger dess radie (d är lika med 2 gånger r).
F: Vilken bokstav använder matematikerna för att beteckna omkrets?
S: Matematiker använder C för omkrets, vilket betyder "runtom".
F: Hur kan vi beräkna arean inom en cirkel?
S: Arean, A, inuti en cirkel kan beräknas genom att multiplicera dess radie med sig själv och sedan multiplicera med ً (A är lika med ً gånger r gånger r).
Sök