Balkteori
Euler-Bernoulli-balkteori (även känd som ingenjörens balkteori eller klassisk balkteori) är en enkel metod för att beräkna böjning av balkar när en belastning läggs på. Detta gäller för små deformationer (hur långt något rör sig) av en balk utan att ta hänsyn till effekterna av skjuvdeformationer. Därför kan den betraktas som ett specialfall av Timosjenkos balkteori. Den introducerades för första gången omkring 1750. Den blev populär under utvecklingen av Eiffeltornet och pariserhjulet i slutet av 1800-talet. Därefter användes den inom många tekniska områden, bland annat maskinteknik och byggteknik. Även om andra avancerade metoder har utvecklats är Euler-Bernoulli-balkteorin fortfarande mycket använd på grund av sin enkelhet.
En vibrerande glasbalk som visar böjningen av balkar som kan uppskattas med hjälp av Euler-Bernoullis balkteori.
Historia
Leonhard Euler och Daniel Bernoulli var de första som sammanställde teorin 1750. På den tiden såg man annorlunda på vetenskap och teknik än i dag. Man litade inte på matematiska teorier som Euler-Bernoulli-balkteorin för praktisk teknisk användning. Broar och byggnader fortsatte att konstrueras med samma metoder fram till slutet av 1800-talet. Det var då Eiffeltornet och pariserhjulet visade teorins giltighet i större skala.
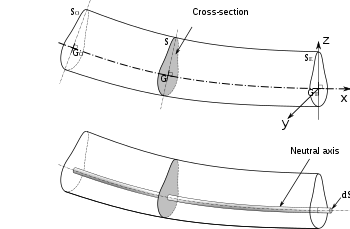
Ritning av ett tvärsnitt av en böjd balk som visar den neutrala axeln.
Statisk balkekvation
Euler-Bernoulli-ekvationen beskriver förhållandet mellan balkens nedböjning och den påförda belastningen enligt nedan:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}\right)=q\,} 
Där w ( x ) {\displaystyle w(x)} 
beskriver balkens nedböjning i z-ledet {\displaystyle z}
vid en viss position x {\displaystyle x}
. q {\displaystyle q}
är en distribuerad belastning, med andra ord en kraft per längdenhet (analogt med att tryck är en kraft per area); den kan vara en funktion av x {\displaystyle x} , w {\displaystyle w} 
eller andra variabler.
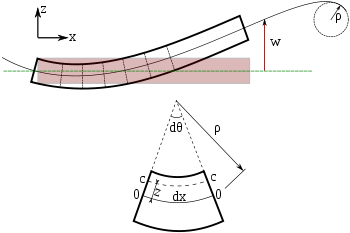
Böjning av en Euler-Bernoulli-balk. Varje tvärsnitt av balken är i 90 grader mot den neutrala axeln.
Frågor och svar
F: Vad är Euler-Bernoulli-balkteorin?
S: Euler-Bernoulli-balkteorin är en enkel metod som används för att beräkna böjning av balkar när en last läggs på, utan att ta hänsyn till effekterna av skjuvdeformationer.
F: När introducerades Euler-Bernoulli-balkteorin för första gången?
S: Euler-Bernoulli-balkteorin introducerades för första gången omkring 1750.
F: Användes Euler-Bernoulli-balkteorin vid utvecklingen av Eiffeltornet och pariserhjulet?
Svar: Ja, Euler-Bernoulli-balkteorin blev populär under utvecklingen av Eiffeltornet och pariserhjulet i slutet av 1800-talet.
F: Inom vilka tekniska områden har Euler-Bernoulli-balkteorin använts?
S: Euler-Bernoulli-balkteorin har använts inom många tekniska områden, bland annat maskinteknik och byggteknik.
F: Används Euler-Bernoulli-balkteorin fortfarande i stor utsträckning i dag?
S: Ja, Euler-Bernoulli-balkteorin används fortfarande i stor utsträckning i dag på grund av sin enkelhet, även om andra avancerade metoder har utvecklats.
F: Vilka typer av böjningar av en balk tillämpas Euler-Bernoulli-balkteorin på?
S: Euler-Bernoulli-balkteorin gäller för små böjningar av en balk.
F: Tar Euler-Bernoulli-balkteorin hänsyn till effekterna av skjuvdeformationer?
S: Nej, Euler-Bernoulli-balkteorin tar inte hänsyn till effekterna av skjuvdeformationer.
