Minkowskis rymdtid – definition och förklaring i speciella relativitetsteorin

Minkowskis rymdtid – tydlig, illustrerad förklaring av fyrdimensionell rymdtid i den speciella relativitetsteorin: definition, metrik och betydelse.

Författare: Leandro Alegsa

I den speciella relativitetsteorin är Minkowskis rymdtid en fyrdimensionell mångfald som introducerades av Hermann Minkowski. Den består av tre rumsdimensioner (x, y, z) och en tidsdimension (t). I den enklaste, platta versionen har rymdtiden metriksignaturen (-+++), vilket betyder att tidskomponenten skiljer sig i tecken från rumsdimensionerna. I den här artikeln kallar vi Minkowskis rymdtid helt enkelt för rymdtid.

Definition och matematisk form

Avståndet mellan två händelser i Minkowskis rymdtid ges av det invarianta intervallet s². I vanliga enheter skrivs detta som

s² = -c²(Δt)² + (Δx)² + (Δy)² + (Δz)²,

där c är ljushastigheten i vakuum och Δt, Δx, Δy, Δz är skillnader i tid och rum mellan de två händelserna. I relativistiska enheter där c = 1 blir uttrycket enklare: s² = - (Δt)² + (Δx)² + (Δy)² + (Δz)².

Metriska tensorn i dessa koordinater kan skrivas som diag(-1, 1, 1, 1). En viktig egenskap är att s² är invariant under Lorentztransformationer — alla inertialsystem kommer överens om värdet av s² mellan två händelser.

Tidslik, rumslik och ljuslik interval

  • Tidslikt (s² < 0): Det finns ett referenssystem där de två händelserna sker på samma plats i rummet. En materia-partikel kan resa mellan händelserna, och man kan definiera ett positivt proper tidsintervall Δτ (egentlig tid) med Δτ² = −s²/c².
  • Ljuslikt (s² = 0): Händelserna är förenade av ett ljus- eller fotonspår. Inga massiva partiklar kan förflytta sig mellan dem, endast ljus.
  • Rumslikt (s² > 0): Händelserna kan inte påverka varandra orsakssambandsmässigt — ingen signal som rör sig långsammare än ljuset kan koppla dem.

Fysisk tolkning

Minkowskis rymdtid ger en geometrisk bild av speciell relativitet: tids- och rumskoordinater kombineras till ett enda fyrdimensionellt objekt. Begrepp som samtidighet blir beroende av referensram: två händelser som är samtidiga i ett inertialsystem behöver inte vara det i ett annat.

Värdet av det invarianta intervallet bestämmer vilket typ av separation två händelser har (tidslik/rumslik/ljuslik) och därmed vilka fysiska processer som är möjliga mellan dem. Proper tid längs en partikels världslinje svarar mot den tid som en observatör bärande partikeln själv upplever.

Minkowski och Lorentztransformationer

Minkowski visade att de transformationer som lämnar intervallet s² oförändrat är de geometriska symmetrierna i rymdtiden — de så kallade Lorentztransformationerna. Dessa kopplar ihop tid och rum på ett sådant sätt att ljushastigheten blir densamma i alla inertialsystem och att fysikens lagar bevaras.

Begränsningar: när rymdtiden är krökt

Minkowskis rymdtid beskriver en platt rymdtid utan gravitation. I närvaro av massor och energi blir rymdtiden krökt och beskrivs istället av den allmänna relativitetsteorin. Där ersätts den konstanta Minkowski-metriken av en rumtidsmetrik som varierar med position, och parallellförflyttning, geodeter och gravitationella effekter måste behandlas med hjälp av Riemanngeometri.

Sammanfattning

Minkowskis rymdtid är en fyrdimensionell, platt geometrisk modell som förenar tid och rum i den speciella relativitetsteorin. Genom det invarianta intervallet s² klassificeras separationen mellan händelser och bestäms vad som är orsaksföljder och vad som inte är det. För gravitationella effekter krävs dock den mera allmänna, krökta beskrivningen i allmänna relativitetsteorin.

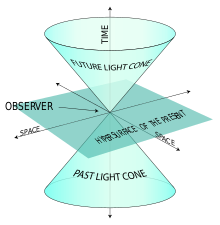
Exempel på en ljuskägel.  Zoom
Exempel på en ljuskägel.  

Definition(er)

Matematisk

Rymdtiden kan ses som ett fyrdimensionellt koordinatsystem där axlarna ges av följande

( c t , x , y , z ) {\displaystyle (ct,x,y,z)} {\displaystyle (ct,x,y,z)}

De kan också betecknas med följande beteckningar

( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} {\displaystyle (x_{1},x_{2},x_{3},x_{4})}

Där x 1 {\displaystyle x_{1}}}{\displaystyle x_{1}} representerar c t {\displaystyle ct}{\displaystyle ct} . Anledningen till att tiden mäts i enheter av ljusets hastighet gånger tidskoordinaten är att tidsenheterna är desamma som rumsenheterna. Rymdtiden har differential för båglängd som ges av

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}} {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}

Detta innebär att rymdtiden har en metrisk tensor som ges av följande

g u v = [ - 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0&0\\0&1&0&0&0\\\0&0&1&0\\\0&0&1\end{bmatrix}}} {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}}

Som tidigare nämnts är rymdtiden platt överallt; i viss mån kan den betraktas som ett plan.

Enkelt

Rymdtiden kan ses som den "arena" där alla händelser i universum äger rum. Allt man behöver för att ange en punkt i rymdtiden är en viss tid och en typisk rumslig orientering. Det är svårt (praktiskt taget omöjligt) att visualisera fyra dimensioner, men en viss analogi kan göras med hjälp av nedanstående metod.



 

Rymdtidsdiagram

Hermann Minkowski införde en viss metod för att grafera koordinatsystem i Minkowskis rumtid. Som framgår av bilden till höger kommer olika koordinatsystem att vara oense om ett föremåls rumsliga orientering och/eller position i tiden. Som du kan se i diagrammet finns det bara en rumslig axel (x-axeln) och en tidsaxel (ct-axeln). Om det behövs kan man införa en extra rumslig dimension (y-axeln), men tyvärr är detta gränsen för antalet dimensioner: det är omöjligt att göra grafer i fyra dimensioner. Regeln för grafer i Minkowskis rymdtid är följande:

1) Vinkeln mellan x-axeln och x'-axeln ges av t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}}{\displaystyle tan(\alpha )={\frac {v}{c}}} där v är objektets hastighet.

2) Ljusets hastighet genom rymdtiden bildar alltid en vinkel på 45 grader med någon av axlarna.



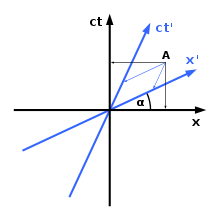
 I relativitetsteorin tilldelar båda observatörerna händelsen i A olika tidpunkter.  Zoom
I relativitetsteorin tilldelar båda observatörerna händelsen i A olika tidpunkter.  

Rymdtid i allmän relativitetsteori

I den allmänna relativitetsteorin använde Einstein ekvationen

G m v = 8 π G T m v {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T} _{mv}} {\displaystyle \mathbb {G} _{mv}=8\pi {\mathcal {G}}\mathbb {T} _{mv}}

För att rymdtiden faktiskt ska kunna kröka sig. Effekterna av detta är gravitationens effekter.



 

Relaterade sidor

Myndighetskontroll: Nationella bibliotek Edit this at Wikidata
  • Frankrike (uppgifter)
  • Tyskland
  • Förenta staterna
  • Lettland
  • Tjeckien


 

Frågor och svar

F: Vad är Minkowskis rymdtid?


S: Minkowskis rymdtid är en fyrdimensionell manifest som skapades av Hermann Minkowski. Den har tre rumsdimensioner (x, y, z) och en tidsdimension.

F: Vad är den metriska signaturen för Minkowskis rumtid?


S: Den metriska signaturen för Minkowskis rymdtid är (-+++).

Fråga: Hur beskriver Minkowskis rymdtid en plan yta?


S: När ingen massa finns närvarande beskriver Minkowskis rymdtid en plan yta.

Fråga: Gäller Minkowskis rymdtid för den allmänna relativitetsteorin?


Svar: Nej, Minkowskis rymdtid gäller endast i den speciella relativitetsteorin. I den allmänna relativitetsteorin används begreppet krökt rumtid för att beskriva effekterna av gravitation och accelererad rörelse.

F: Hur många dimensioner har Minkowskis rumtid?


S: Minkowsi rymdtid har fyra dimensioner - tre rymddimensioner (x, y, z) och en tidsdimension.

F: Vem skapade begreppet Minkowsi Spacetime?


S: Hermann Minkowksi skapade begreppet MInkowskis rymdtid.


Sök
AlegsaOnline.com - 2020 / 2025 - License CC3