Rumtid: Vad är det? Definition, Minkowski och relativitet
Rumtid: tydlig förklaring av begreppet, Minkowskis fyrdimensionella rum och relativitetsteorins konsekvenser — definition, exempel och betydelse för universum.
Rymd-tid är en matematisk modell som förenar rum och tid till en enda idé som kallas kontinuum. Detta fyrdimensionella kontinuum är känt som Minkowskis rum. I denna bild behandlas tid som en fjärde dimension som tillsammans med de tre rumsdimensionerna bildar en enhetlig struktur där händelser (punkter i rumtid) kan beskrivas med fyra koordinater.
Minkowski, metrik och invarianta intervall
I Minkowskis rum är det centrala begreppet det invarianta intervallet mellan två händelser. Intervallet är ett kvantitativt mått som är samma för alla inertialsystem (dvs. observatörer i likformig rörelse). I enklaste form kan intervallet skrivas som
s² = -c²(Δt)² + (Δx)² + (Δy)² + (Δz)²,
där c är ljushastigheten, Δt tidsintervallet och Δx, Δy, Δz rumsförskjutningarna mellan händelserna (konventioner för teckensnitt kan variera: vissa författare skriver +c²Δt² − Δx² − ...). Att intervallet är invariant betyder att dess värde inte ändras under Lorentztransformationer — de koordinattransformationer som kopplar ihop olika inertialsystem i speciella relativitetsteorin.
Ljuskägla och kausalitet
Intervallet delar in relationen mellan händelser i tre kategorier:
- Tidlik (s² < 0 enligt ovanstående konvention): en händelse kan påverka en annan genom en fysisk signal som färdas långsammare än ljuset.
- Rumslik (s² > 0): händelser ligger utanför varandras ljuskäglor och kan inte orsaka varandra.
- Ljuslik (s² = 0): händelser kopplade av en ljussignal (på ljuskäglan).
Denna uppdelning ger en tydlig geometrisk bild av kausalitet i ett relativistiskt universum: bara händelser inom den framtida ljuskäglan kan påverkas av en given händelse.
Relativitetseffekter: tiddilatation och längdkontraktion
En viktig följd av rumtidens geometri är att tid och rum inte är absoluta. I den icke-relativistiska klassiska mekaniken är det bra att använda euklidisk rymd i stället för rumtid, eftersom tiden behandlas som universell. Men i ett relativistiskt universum kan tiden inte skiljas från de tre dimensionerna av rymden. Detta beror på att den observerade hastigheten med vilken tiden går beror på ett objekts hastighet i förhållande till observatören.
Två av de mest kända effekterna är:
- Tiddilatation: en klocka som rör sig relativt en observatör går långsammare enligt observatören. Kvantitativt ges detta av Δt' = γ Δt, där γ = 1 / sqrt(1 − v²/c²) är Lorentzfaktorn och v är relativ hastighet.
- Längdkontraktion: objekt som rör sig i förhållande till en observatör mäts kortare i rörelseriktningen: L = L0 / γ, där L0 är objektets längd i dess eget vilosystem.
Gravitation och allmän relativitet
Effekter av gravitation beskrivs bättre i Einsteins allmänna relativitetsteori, där gravitation inte är en kraft i traditionell mening utan uttryck för rumtidens krökning orsakad av massa och energi. Styrkan hos ett gravitationsfält fördröjer också tidens gång för ett objekt sett av en observatör utanför fältet — detta kallas gravitationell tidsdilatation och är experimentellt verifierat (t.ex. i atomklockor på olika höjder och i GPS-systemet, som måste kompensera både speciella och allmänna relativitetseffekter).
Minkowskis rum är en modell för platt rumtid (ingen massa/energi som kröker rummet). När massor finns med blir rumtiden krökt och beskrivs av metriska tensorer i allmän relativitet.
Tillämpningar och observationer
Begreppet rumtid är centralt för modern fysik och kosmologi. Kombinationen av dessa idéer hjälpte kosmologin att förstå hur universum fungerar på stor nivå (t.ex. galaxer) och på liten nivå (t.ex. atomer). Relativistiska beräkningar används också i tekniska system (GPS), partikelfysik (partiklar nära ljusets hastighet) och i analys av svarta hål och gravitationsvågor.
Sammanfattning
Rumtid är en geometrisk ram som förenar rum och tid till ett enda fyrdimensionellt kontinuum. I den speciella relativitetsteorin är detta kontinuum platt och beskrivs av Minkowskis rum och ett invariant intervall bevarat av Lorentztransformationer. I närvaro av massa och energi kröks rumtiden och beskrivs av allmän relativitet, vilket leder till fenomen som gravitationell tidsdilatation och böjning av ljus.
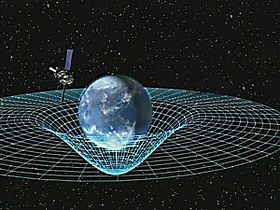
En illustration av den krökning av rymdtiden som orsakas av jorden.
Ytterligare aspekter
Överallt där det finns materia böjer den rymdtidens geometri. Detta resulterar i en krökt form av rumtiden som kan förstås som gravitation. De vita linjerna på bilden till höger representerar massans effekt på rumtiden.
I den klassiska mekaniken är användningen av rymdtid frivillig, eftersom tiden är oberoende av rörelsen i den euklidiska rummets tre dimensioner. När en kropp rör sig med hastigheter som ligger nära ljusets hastighet (relativistiska hastigheter) kan tiden dock inte separeras från rummets tre dimensioner. Tiden, från en stationär observatörs synvinkel, beror på hur nära ljusets hastighet föremålet rör sig.
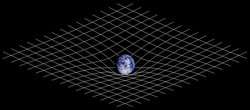
Tvådimensionell analogi av rymdtidsförvrängning
Historiskt ursprung
Många förknippar rymdtid med Albert Einstein, som föreslog den speciella relativitetsteorin 1905. Det var dock Einsteins lärare Hermann Minkowski som föreslog rumtiden i en uppsats från 1908. Hans begrepp Minkowskis rum är den tidigaste behandlingen av rum och tid som två aspekter av en enhetlig helhet, vilket är kärnan i den speciella relativitetsteorin. Han hoppades att denna nya idé skulle klargöra den speciella relativitetsteorin.
Minkowskis rymdtid är endast korrekt när det gäller att beskriva konstant hastighet. Det var dock Einstein som upptäckte rymdtidens krökning (gravitation) i den allmänna relativitetsteorin. I den allmänna relativitetsteorin generaliserade Einstein Minkowskis rumtid för att inkludera effekterna av acceleration. Einstein upptäckte att krökningen i hans 4-dimensionella representation av rumtiden faktiskt var orsaken till gravitationen.
Den trettonde upplagan av Encyclopedia Britannica från 1926 innehöll en artikel av Einstein med titeln "space-time".
Litterär bakgrund
Edgar Allan Poe skrev en essä om kosmologi med titeln Eureka (1848) där det står att "rymd och varaktighet är ett". Detta är det första kända exemplet på att rymd och tid är olika uppfattningar om en sak. Poe kom fram till denna slutsats efter cirka 90 sidor av resonemang, men använde ingen matematik.
År 1895 skrev H.G. Wells i sin roman Tidsmaskinen: "Det finns ingen skillnad mellan tiden och någon av rummets tre dimensioner, förutom att vårt medvetande rör sig längs den". Han tillade: "Vetenskapsmännen vet mycket väl att tiden bara är ett slags rymd".
Rymdtid inom kvantmekaniken
I den allmänna relativitetsteorin betraktas rymdtiden som jämn och kontinuerlig. I den kvantmekaniska teorin är rymdtiden dock inte alltid kontinuerlig.
Relaterade sidor
- Dimension
- Manifold
Frågor och svar
F: Vad är rymdtid enligt texten?
S: Rymd-tid är en matematisk modell som kopplar samman rum och tid och bildar ett fyrdimensionellt kontinuum som kallas Minkowski-rymden.
F: Hur har kombinationen av rum och tid hjälpt kosmologin?
S: Kombinationen av rymd och tid har gjort det möjligt för kosmologin att bättre förstå hur universum fungerar på både den stora nivån, t.ex. galaxer, och den lilla nivån, t.ex. atomer.
F: Varför är det bra att använda euklidisk rymd istället för rumtid i icke-relativistisk klassisk mekanik?
S: I icke-relativistisk klassisk mekanik är det bra att använda euklidisk rymd eftersom tiden behandlas som universell med en konstant hastighet som är oberoende av observatörens rörelsetillstånd.
F: Varför är tiden oskiljaktig från de tre rumsdimensionerna i ett relativistiskt universum?
S: Tiden kan inte separeras från de tre rumsdimensionerna i ett relativistiskt universum eftersom den observerade hastigheten med vilken tiden går beror på ett objekts hastighet i förhållande till observatören.
F: Hur påverkar styrkan hos ett gravitationsfält tidsförloppet för ett objekt?
S: Styrkan i ett gravitationsfält saktar ner tidens gång för ett objekt som ses av en observatör utanför fältet.
F: Vad kallas det fyrdimensionella kontinuum som förenar tid och rum?
S: Det fyrdimensionella kontinuum som förenar tid och rum kallas Minkowski-rymden.
F: Hur har kombinationen av rum och tid hjälpt kosmologin att förstå universum?
S: Kombinationen av rymd och tid har hjälpt kosmologin att bättre förstå hur universum fungerar, både på den stora nivån, som galaxer, och på den lilla nivån, som atomer.
Sök