Högerhandsregeln: Så bestämmer du riktningen på vektorers korsprodukt
Lär dig Högerhandsregeln för korsprodukt: enkel steg-för-steg-guide som visar hur du bestämmer riktningen på vektorers korsprodukt snabbt och säkert.
Högerregeln är en enkel och användbar konvention inom vektormatiken. Den hjälper dig att komma ihåg riktningen för korsprodukten (vektorprodukten) mellan två vektorer: resultatvektorn står vinkelrät mot planet som bildas av de två ursprungliga vektorerna och dess riktning bestäms av högerhanden.
- Forma din högra hand så att fingrarna kan stå i tre olika riktningar som är i rät vinkel mot varandra.
- Sträck ut pekfingret i den ena riktningen och håll tummen rakt upp som när du formar en pistol. (Tummen, pekfingret och långfingret ska vara ungefär i 90° mot varandra.)
- Rikta tummen i riktning mot den första vektorn (A) och pekfingret i riktning mot den andra vektorn (B). Då pekar långfingret i riktningen för korsprodukten A × B.
Kom ihåg att ordningen spelar roll: om du byter plats på vektorerna vänder riktningen på resultatet. Med andra ord gäller
A × B = − (B × A)
Rent geometriskt är A × B en vektor som är vinkelrät mot både A och B, med storleken
|A × B| = |A| |B| sin(θ),
där θ är vinkeln mellan A och B. Om A och B är parallella (θ = 0° eller 180°) blir korsprodukten noll eftersom sin(θ) = 0.
Exempel i ett kartesiskt koordinatsystem med enhetsvektorerna i, j och k (eller e_x, e_y, e_z):
- i × j = k
- j × i = −k
Användningsområden: korsprodukten används bland annat för att beräkna moment (vridmoment) τ = r × F, den magnetiska kraften F = q v × B på en laddning i ett magnetfält, och arean av parallellogrammet som spänns upp av två vektorer (arean = |A × B|).
Praktiska tips: om du vill vara säker på tecknet, håll alltid höger hand och tänk "tummen först" — rikta tummen längs den första vektorn (A), pekfingret längs den andra (B) och läs av långfingret som A × B.

Högerhandregeln för rörelser som produceras med skruvgängor

Den vänsterhänta orienteringen visas till vänster och den högerhänta till höger.
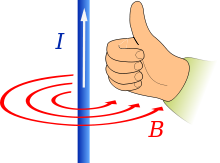
Förutsägelse av fältets riktning (B) när strömmen I flyter i riktning mot tummen.
Variationer
Det finns en annan regel som kallas högergreppsregeln (eller korkskruvsregeln) och som används för magnetfält och saker som roterar.
1. Börja med att lägga ut höger hand och rikta tummen rakt ut så att den står i rät vinkel mot de andra fingrarna.
2. Knyt nu fingrarna till en knytnäve och håll tummen utåt (som en tumme upp).
3. Anpassa hur dina fingrar krullar sig till hur något rör sig. Den riktning som din tumme pekar i är riktningen för den vektor som vi använder för att tala om det.
Du kan göra det omvänt genom att börja tummen i vektorns riktning och se hur fingrarna kröker sig för att se rotationsriktningen. Om du pekar med tummen i strömriktningen i en tråd är magnetfältet som uppstår runt den i riktning mot dina krökande fingrar.
Frågor och svar
F: Vad är högerregeln?
S: Högerregeln är en konvention i vektormatematik som hjälper dig att komma ihåg riktningen när vektorer korsmultipliceras.
F: Hur använder man högerregeln för att räkna ut riktningen för en korsprodukt?
S: För att räkna ut riktningen för en korsprodukt ska du stänga din högra hand och sträcka ut pekfingret. Sträck tummen rakt uppåt som om du gjorde tecknet för en pistol. Rikta din "pistol" rakt fram och stick sedan ut ditt långfinger så att det pekar åt vänster och alla dina fingrar står i rät vinkel mot varandra. Rikta tummen i den första vektorns riktning och peka med pekfingret i den andra vektorns riktning. Ditt långfinger pekar i riktning mot korsprodukten.
F: Vad händer om du ändrar ordningen när vektorer korsmultipliceras?
S: När du ändrar ordningen när vektorerna korsmultipliceras, går resultatet i motsatt riktning. Därför är det viktigt att se till att du går i ordningen tumme x pekare = mitt .
F: Vad betyder den här ekvationen? {\displaystyle {\vec {thumb}}\times {\vec {pointer}}={\vec {middle}}} .
S: Denna ekvation betyder att om två vektorer korsas multipliceras med varandra (tumme x pekare), så kommer det att resultera i en tredje vektor (mitten).
Sök
