Korsprodukt

Korsprodukten är en matematisk operation som kan utföras mellan två vektorer. Efter att ha utfört korsprodukten bildas en ny vektor. Korsprodukten av två vektorer är alltid vinkelrät mot båda de vektorer som "korsades". Detta innebär att korsprodukten alltid måste användas i tredimensionella rum.

Korsproduktens betydelse

Eftersom korsprodukten är en vektoroperation är den extremt viktig inom alla vetenskaper (särskilt fysik), teknik och matematik. Ett viktigt exempel på korsprodukt är vridmoment eller moment. Ett annat viktigt användningsområde är magnetfältet.

Visualisering av korsprodukten i tre dimensioner

Korsprodukten av a → {\displaystyle {\vec {a}}} ${\vec {a}}$ och b → {\displaystyle {\vec {b}}} ${\vec {b}}$ är en vektor som vi kallar c → {\displaystyle {\vec {c}}} ${\vec {c}}$ :

c → = a → × b → {\displaystyle {\vec {c}}={\vec {a}}\times {\vec {b}}} ${\vec {c}}={\vec {a}}\times {\vec {b}}$

Storleken på c → {\displaystyle {\vec {c}}}} ${\vec {c}}$ ges då av:

c = | c → | = | a → | | b → | sin θ = a b sin θ {\displaystyle c=|{\vec {c}}|=|{\vec {a}}||{\vec {b}}|\sin \theta =ab\sin \theta } $c=|{\vec {c}}|=|{\vec {a}}||{\vec {b}}|\sin \theta =ab\sin \theta$ ,

där θ {\displaystyle \theta } $\theta$ är vinkeln mellan a → {\displaystyle {\vec {a}}} ${\vec {a}}$ och b → {\displaystyle {\vec {b}}} ${\vec {b}}$ . Vektorn a → × b → {\displaystyle {\vec {a}}\times {\vec {b}}} ${\vec {a}}\times {\vec {b}}$ är vinkelrät mot både a → {\displaystyle {\vec {a}}} ${\vec {a}}$ och b → {\displaystyle {\vec {b}}} ${\vec {b}}$ . Riktningen för a → × b → {\displaystyle {\vec {a}}\times {\vec {b}}} ${\vec {a}}\times {\vec {b}}$ bestäms genom en variant av högerregeln. Om du håller din högra hand så som visas i figuren är tummen i riktning mot c → {\displaystyle {\vec {c}}} ${\vec {c}}$ , pekfingret pekar i riktning mot a → {\displaystyle {\vec {a}}} ${\vec {a}}$ och ditt andra finger pekar i riktning mot b → {\displaystyle {\vec {b}}} ${\vec {b}}$ . Om vinkeln mellan ditt pekfinger och ditt andra finger är större än 180° måste du vända handen upp och ner.

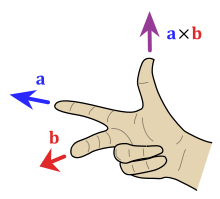
Hitta riktningen på korsprodukten.

Hur man beräknar korsprodukten i vektornotation

Liksom alla matematiska operationer kan korsprodukten göras på ett enkelt sätt.

Två dimensioner

Om
a → = ⟨ a 1 , a 2 ⟩ {\displaystyle {\vec {a}}=\langle a_{1},a_{2}\rangle } ${\vec {a}}=\langle a_{1},a_{2}\rangle$
och
b → = ⟨ b 1 , b 2 ⟩ {\displaystyle {\vec {b}}=\langle b_{1},b_{2}\rangle } ${\vec {b}}=\langle b_{1},b_{2}\rangle$
då
a → × b → = ( a 1 b 2 - a 2 b 1 ) k ^ {\displaystyle {\vec {a}}\times {\vec {b}}=(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}} ${\vec {a}}\times {\vec {b}}=(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}$

eller

a → × b → = c → {\displaystyle {\vec {a}}\times {\vec {b}}={\vec {c}}} ${\vec {a}}\times {\vec {b}}={\vec {c}}$
och
c → = ⟨ 0 , 0 , a 1 b 2 - a 2 b 1 ⟩ = ( a 1 b 2 - a 2 b 1 ) k ^ {\displaystyle {\vec {c}}=\langle 0,0,a_{1}b_{2}-a_{2}b_{1}\rangle =(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}} ${\vec {c}}=\langle 0,0,a_{1}b_{2}-a_{2}b_{1}\rangle =(a_{1}b_{2}-a_{2}b_{1}){\hat {k}}$

k ^ {\displaystyle {\hat {k}}}} ${\hat {k}}$ är bara en symbol som säger att vår nya vektor pekar uppåt (i z-riktningen). Om du "korsar" två vektorer som båda befinner sig i x-y-planet kommer produkten alltid att vara vinkelrät mot båda vektorerna, och om båda vektorerna befinner sig i x-y-planet är det enda sättet att vara vinkelrät mot båda vektorerna att vara i z-riktningen. Om värdet av a 1 b 2 - a 2 b 1 {\displaystyle a_{1}b_{2}-a_{2}b_{1}}} $a_{1}b_{2}-a_{2}b_{1}$ är positivt pekar den ut ur sidan; om värdet är negativt pekar den in i sidan.

Tre dimensioner

Om
a → = ⟨ a 1 , a 2 , a 3 ⟩ {\displaystyle {\vec {a}}=\langle a_{1},a_{2},a_{3}\rangle } ${\vec {a}}=\langle a_{1},a_{2},a_{3}\rangle$
och
b → = ⟨ b 1 , b 2 , b 3 ⟩ {\displaystyle {\vec {b}}=\langle b_{1},b_{2},b_{3}\rangle } ${\vec {b}}=\langle b_{1},b_{2},b_{3}\rangle$
då
a → × b → = ⟨ a 2 b 3 - a 3 b 2 , a 3 b 1 - a 1 b 3 , a 1 b 2 - a 2 b 1 ⟩ {\displaystyle {\vec {a}}\times {\vec {b}}=\langle a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1}\rangle } ${\vec {a}}\times {\vec {b}}=\langle a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1}\rangle$

Grundläggande egenskaper hos korsprodukten

a → × b → = - b → × a → {\displaystyle {\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}} ${\vec {a}}\times {\vec {b}}=-{\vec {b}}\times {\vec {a}}$

a → × ( b → + c → ) = a → × b → + a → × c → {\displaystyle {\vec {a}}\times ({\vec {b}}+{\vec {c}}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}}} ${\vec {a}}\times ({\vec {b}}+{\vec {c}})={\vec {a}}\times {\vec {b}}+{\vec {a}}\times {\vec {c}}$

c ( a → × b → ) = ( c a → ) × b → = a → × ( c b → ) {\displaystyle c({\vec {a}}\times {\vec {b}})=(c{\vec {a}})\times {\vec {b}}={\vec {a}}\times (c{\vec {b}})} $c({\vec {a}}\times {\vec {b}})=(c{\vec {a}})\times {\vec {b}}={\vec {a}}\times (c{\vec {b}})$

Frågor och svar

F: Vad är korsprodukten?

S: Korsprodukten är en matematisk operation som kan göras mellan två tredimensionella vektorer.

F: Hur representeras ofta korsprodukten?

S: Korsprodukten representeras ofta av symbolen × eller \times.

F: Vad händer efter att man har utfört korsprodukten?

S: Efter att ha utfört korsprodukten bildas en ny vektor.

F: Vad är förhållandet mellan korsproduktvektorn och de vektorer som "korsades"?

S: Korsprodukten av två vektorer är alltid vinkelrät (den bildar en hörnformad vinkel) mot båda de vektorer som "korsades".

F: I vilken dimension fungerar normalt korsprodukten?

S: Korsprodukten fungerar normalt endast i tredimensionella rum.

F: Vilka är de tre dimensioner där korsprodukt kan utföras?

S: De tre dimensioner där korsprodukt kan utföras är upp eller ner, vänster eller höger, samt framåt eller bakåt.

F: Varför kan korsprodukt normalt bara fungera i tredimensionell rymd?

S: Korsprodukt fungerar normalt bara i tredimensionell rymd eftersom det är de dimensioner där du kan gå upp eller ner, vänster eller höger, och framåt eller bakåt.