Vektor – definition, riktning och magnitud | Matematik & fysik

Lär dig vad en vektor är: definition, riktning och magnitud med klara förklaringar, exempel och illustrationer för matematik & fysik.

Författare: Leandro Alegsa

15-02-2026 21:31

A vector

En vektor är ett matematiskt objekt som har en storlek (magnitud) och en riktning. Den representeras ofta av feta bokstäver (t.ex. u {\displaystyle \mathbf {u} } $\mathbf {u}$ , v {\displaystyle \mathbf {v} } $\mathbf {v}$ , w {\displaystyle \mathbf {w} , w {\displaystyle \mathbf {w} } $\mathbf {w}$ ), eller som ett linjesegment från en punkt till en annan (som i A B → {\displaystyle {\overrightarrow {AB}}} ${\overrightarrow {AB}}$ ).

En vektor kan till exempel användas för att visa avståndet och riktningen i vilken något rör sig. Om man frågar efter riktningar och säger "Gå en kilometer mot norr" är det en vektor, men om man säger "Gå en kilometer" utan att ange en riktning är det en skalär.

Vanligtvis ritar vi vektorer som pilar. Pilens längd är proportionell mot vektorns storlek. Den riktning som pilen pekar mot är vektorns riktning.

Komponenter och koordinater

En vektor i planet (2D) kan beskrivas med två komponenter, till exempel v = (v_x, v_y). I rummet (3D) används tre komponenter: v = (v_x, v_y, v_z). Komponenterna är koordinaterna för vektorn i en vald bas (vanligtvis standardbasen).

Man kan också skriva vektorer som kolumner eller rader i matrisform. I analys och linjär algebra är detta praktiskt när man ska utföra operationer eller byta koordinatsystem.

Längd (magnitud) och enhetsvektor

Vektorns längd, eller magnitud, betecknas ofta |v| och beräknas i 2D som |v| = sqrt(v_x^2 + v_y^2) och i 3D som |v| = sqrt(v_x^2 + v_y^2 + v_z^2). En enhetsvektor är en vektor med längd 1 och fås genom att dela en vektor med dess magnitud: u = v / |v| (förutsatt att v ≠ 0).

Addition och skalärmultiplikation

Vektoraddition: Två vektorer adderas komponentvis: (a_x, a_y) + (b_x, b_y) = (a_x + b_x, a_y + b_y). Geometriskt motsvarar detta att lägga pilar "ände till början".
Skalärmultiplikation: Multiplicera en vektor med ett reellt tal (skalär) ändrar dess längd och ibland riktning: c(a_x, a_y) = (c a_x, c a_y). Om c < 0 vänder riktningen.

Skalärprodukt och vektorprodukt

Skalärprodukt (dotprodukt) mellan v och w i 3D är v·w = v_x w_x + v_y w_y + v_z w_z. Den kan också uttryckas som v·w = |v||w| cos θ, där θ är vinkeln mellan v och w. Dotprodukten ger ett skalärvärde och används för att bestämma vinklar och projektioner.

Vektorprodukt (kryssprodukt) är definierad i 3D och ger en vektor som är vinkelrät mot både v och w. Dess längd är |v × w| = |v||w| sin θ och riktningen bestäms av högerhandsregeln. I 2D används kryssprodukt inte på samma sätt, men man kan betrakta en "skalär kryssprodukt" genom att införliva en tredje dimension.

Geometriska tolkningar och exempel

Displacement (förflyttning): Vektorer beskriver hur långt och i vilken riktning ett objekt förflyttas.
Hastighet och acceleration: Inom fysiken är hastighet en vektor (storlek + riktning). Exempel: "20 m/s nordost".
Kraft: Krafters storlek och riktning anges med vektorer. Resultanten av flera krafter fås genom vektoraddition.

Egenskaper och viktiga begrepp

Nollvektorn: Den vektor som har alla komponenter 0, betecknas 0. Den har ingen riktning och längd 0.
Negativ vektor: För varje vektor v finns en -v som har samma längd men motsatt riktning.
Linjära kombinationer: Kombinationer a v + b w är centrala i linjär algebra — vektorer kan kombineras med skalärer för att bilda nya vektorer.
Parallellism och ortogonalitet: Två vektorer är parallella om den ena är en skalär gånger den andra; de är ortogonala (vinkelräta) om deras dotprodukt är noll.

Övningsexempel

1) Givet v = (3, 4), beräkna |v|. Svar: |v| = sqrt(3^2 + 4^2) = 5.

2) Givet v = (1, 2, 2) och w = (2, 0, 1), beräkna v·w. Svar: v·w = 1·2 + 2·0 + 2·1 = 4.

Sammanfattningsvis är vektorer grundläggande i både matematik och fysik eftersom de kombinerar storlek och riktning. De används för att beskriva lägen, rörelser, krafter och mycket mer, och de följer enkla algebraiska regler som gör dem lätta att manipulera både geometriskt och analytiskt.

Exempel på vektorer

John går 20 meter norrut. Riktningen "norr" tillsammans med avståndet "20 meter" är en vektor.
Ett äpple faller ner med 10 meter per sekund. Riktningen "nedåt" i kombination med hastigheten "10 meter per sekund" är en vektor. Denna typ av vektor kallas också hastighet.

Exempel på skalarer

Avståndet mellan två platser är 10 kilometer. Detta avstånd är inte en vektor eftersom det inte innehåller någon riktning.
Antalet frukter i en låda är inte en vektor.
En person som pekar är inte en vektor eftersom det bara finns en riktning. Det finns ingen storlek (avståndet från personens finger till en byggnad, till exempel).
Längden på ett objekt.
En bil kör i 100 kilometer i timmen. Detta beskriver inte en vektor, eftersom det bara finns en storlek, men ingen riktning.

Fler exempel på vektorer

Förskjutning är en vektor. Förskjutning är den sträcka som något rör sig i en viss riktning. Ett mått på enbart avstånd är en skalär.
En kraft som innehåller en riktning är en vektor.
Hastigheten är en vektor, eftersom den är en hastighet i en viss riktning.
Acceleration är hastighetsförändringen. Ett föremål accelererar om det ändrar hastighet eller riktning.

Hur man lägger till vektorer

Lägg till vektorer på papper med hjälp av huvud till svans-metoden

Metoden Head to Tail för att addera vektorer är användbar för att göra en uppskattning på papper av resultatet av att addera två vektorer. Så här gör du:

Varje vektor ritas som en pil med en viss längd bakom sig, där varje längdenhet på pappret representerar en viss storlek på vektorn.
Rita nästa vektor, med den andra vektorns svans (ände) vid den första vektorns huvud (framsida).
Upprepa för alla ytterligare vektorer: Dra nästa vektors svans i huvudet på den föregående vektorn.
Dra en linje från den första vektorns svans till den sista vektorns huvud - det är resultanten (summan) av alla vektorerna.

Det kallas "Head to Tail"-metoden, eftersom varje huvud från den föregående vektorn leder till svansen i nästa vektor.

Användning av komponentformulär

^{[behöver förklaras ]}

Att använda komponentformen för att addera två vektorer innebär bokstavligen att man adderar vektorernas komponenter för att skapa en ny vektor. Låt till exempel a och b vara två tvådimensionella vektorer. Dessa vektorer kan skrivas i termer av deras komponenter.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})} $\mathbf {a} =(a_{x},a_{y})$

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})} $\mathbf {b} =(b_{x},b_{y})$

Anta att c är summan av dessa två vektorer, så att c = a + b. Detta innebär att c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} $\mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})$ .

Här är ett exempel på addition av två vektorer med hjälp av deras komponentformer:

a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)} $\mathbf {a} =(3,-1)$

b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)} $\mathbf {b} =(2,2)$

c = a + b = ( a x + b x , a y + b y ) = ( 3 + 2 , - 1 + 2 ) = ( 5 , 1 ) {\displaystyle {\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}} ${\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}$

Den här metoden fungerar för alla vektorer, inte bara tvådimensionella.

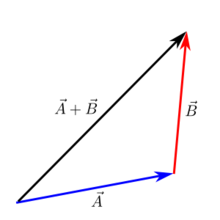
Tillägg från huvud till svans

Hur man multiplicerar vektorer

Med hjälp av punktprodukten

Punktprodukten är en metod för att multiplicera vektorer. Den ger en skalär. Den använder komponentform:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ ${\begin{aligned}\mathbf {a} &=(2,3)\\\mathbf {b} &=(1,4)\\\mathbf {a} \cdot \mathbf {b} &=(2,3)\cdot (1,4)\\&=(2\cdot 1)+(3\cdot 4)\\&=2+12\\&=14\end{aligned}}$

Användning av korsprodukten

Korsprodukten är en annan metod för att multiplicera vektorer. Till skillnad från punktprodukten ger den en vektor. Med hjälp av komponentformen:

a × b = | a | | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} } $\mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n}$

Här är | a | {\displaystyle |\mathbf {a} |} $|\mathbf {a} |$ betyder längden på en {\displaystyle \mathbf {a} } $\mathbf {a}$ och n {\displaystyle \mathbf {n} } $\mathbf {n}$ är enhetsvektorn i rät vinkel mot både en {\displaystyle \mathbf {a} } $\mathbf {a}$ och b {\displaystyle \mathbf {b} } $\mathbf {b}$ .

Multiplicering med en skalär

För att multiplicera en vektor med en skalär (ett normalt tal) multiplicerar du talet med varje komponent i vektorn:

c x = ( c x 1 , c x 2 , . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})} $c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})$

Ett exempel på detta är

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ ${\begin{aligned}c&=5\\\mathbf {x} &=(3,4)\\c\,\mathbf {x} &=(5\cdot 3,5\cdot 4)\\&=(15,20)\end{aligned}}$

Relaterade sidor

Analytisk geometri
Nollvektor
Enhetsvektor
Vektorfält
Vektorgrafik
Vektorrum
Vektorsubrymd

Frågor och svar

F: Vad är en vektor?

S: En vektor är ett matematiskt objekt som har en storlek, kallad magnitud, och en riktning. Det representeras ofta av feta bokstäver eller som ett linjesträck från en punkt till en annan.

F: Hur brukar vi rita vektorer?

S: Vi brukar rita vektorer som pilar. Längden på pilen är proportionell mot vektorns magnitud och riktningen som pilen pekar mot är vektorns riktning.

F: Vad betyder det när någon frågar efter vägbeskrivningar?

S: Om någon säger "Gå en kilometer mot norr" är det en vektor, men om han eller hon säger "Gå en kilometer" utan att ange en riktning är det en skalär.

F: Vilka är några exempel på hur vektorer kan användas?

S: Vektorer kan användas för att visa avståndet och riktningen för något som rört sig. De kan också användas när man frågar efter vägbeskrivningar eller när man navigerar i ett område.

F: Hur representeras vektorer matematiskt?

S: Vektorer representeras ofta med fetstil (t.ex. u, v, w) eller som ett linjesträck från en punkt till en annan (t.ex. A→B).

F: Vad betyder det när något kallas skalär?

S: När något kallas skalärt betyder det att det inte finns någon riktningsinformation kopplad till det, utan endast numeriska värden som avstånd eller hastighet.

Sök