Histogram
Ett histogram är ett begrepp från statistiken. Det är en grafisk bild som berättar om fördelningen av de berörda proverna. De är vanligen en bild som görs av en tabell med många kategorier. I tabellen står det hur många prover det finns i varje kategori.
Ordet histogram kommer från histos och gramma på grekiska. Histos betyder väv eller mast. Gramma betyder ritning, anteckning eller skrivning. Ett histogram av något är därför etymologiskt sett en ritning av detta väv.
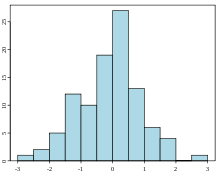
Exempel på ett histogram med 100 normalfördelade slumpmässiga värden.
Liknande idéer
Histogrammet är ett av de sju grundläggande verktygen för kvalitetskontroll, som även omfattar Paretodiagram, kontrollblad, kontrolldiagram, orsaks- och effektdiagram, flödesschema och spridningsdiagram.
En generalisering av histogrammet är kärnutjämningstekniker. På så sätt konstrueras en jämn sannolikhetstäthetsfunktion från de tillhandahållna uppgifterna.
Frågor och svar
F: Vad är ett histogram?
S: Ett histogram är en grafisk display som berättar om fördelningen av de inblandade proverna.
F: Vad är syftet med ett histogram?
S: Syftet med ett histogram är att visa fördelningen av de aktuella proverna.
F: Vad betyder ordet histogram?
S: Ordet histogram kommer från grekiskans histos och gramma. Histos betyder väv eller mast. Gramma betyder ritning, protokoll eller skrift.
F: Vad betyder termen "histos" på grekiska?
S: Termen "histos" betyder väv eller mast på grekiska.
F: Vad betyder termen "gramma" på grekiska?
S: Termen "gramma" betyder ritning, uppteckning eller skrift på grekiska.
F: Vad är en vanlig egenskap hos ett histogram?
S: En vanlig egenskap hos ett histogram är att det är en bild som är gjord av en tabell med många kategorier.
F: Vilken information ger en histogramtabell?
S: En histogramtabell ger information om hur många prover det finns i varje kategori.
