Sannolikhetstäthetsfunktion (PDF) – definition, egenskaper och exempel
Lär dig allt om sannolikhetstäthetsfunktion (PDF): definition, viktiga egenskaper, integration och tydliga exempel för kontinuerliga sannolikhetsfördelningar.
Inom sannolikhet och statistik är en sannolikhetstäthetsfunktion en funktion som karakteriserar en kontinuerlig sannolikhetsfördelning. För en slumpmässig variabel X skrivs sannolikhetstäthetsfunktionen för X ibland som 
. Integralen av sannolikhetstäthetsfunktionen i intervallet ![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
ger sannolikheten för att en given slumpvariabel med den givna tätheten ingår i det angivna intervallet. Per definition är sannolikhetsdensitetsfunktionen icke-negativ i hela sitt område, där integralen summerar till 1.
Formellt krav och grundläggande egenskaper
- Icke-negativitet: f_X(x) ≥ 0 för alla x.
- Normalisering: ∫_{-∞}^{∞} f_X(x) dx = 1.
- Sannolikhet för intervall: För a ≤ b gäller P(a ≤ X ≤ b) = ∫_a^b f_X(x) dx.
- P(något exakt värde): För en kontinuerlig variabel är P(X = x) = 0 för varje enskilt x (eftersom integralen över en punkt är noll).
- Support: Mängden där f_X(x) > 0 kallas för variabelns support.
- PDF kan vara större än 1: Värdet f_X(x) kan överskrida 1 på vissa intervall; det är integralens värde över ett intervall som representerar sannolikhet, inte funktionen i en punkt.
Relation till fördelningsfunktion (CDF)
Den kumulativa fördelningsfunktionen (CDF) definieras som F_X(x) = P(X ≤ x). För en kontinuerlig variabel är sambandet mellan PDF och CDF
F_X(x) = ∫_{-∞}^{x} f_X(t) dt.
Om f_X är kontinuerlig gäller f_X(x) = dF_X(x)/dx, det vill säga PDF är derivatan av CDF.
Förväntningsvärde, varians och moment
Momenter beräknas med hjälp av PDF:
- Förväntningsvärde (medelvärde): E[X] = ∫_{-∞}^{∞} x f_X(x) dx, förutsatt att integralen konvergerar.
- Varians: Var(X) = E[(X − μ)^2] = ∫_{-∞}^{∞} (x − μ)^2 f_X(x) dx där μ = E[X].
- Allmän moment: E[X^k] = ∫ x^k f_X(x) dx.
Vanliga exempel på PDF:er
- Uniformfördelning på [a, b]: f(x) = 1/(b−a) för a ≤ x ≤ b, annars 0. Exempel: för [0,1] är f(x)=1 och P(0.2≤X≤0.5)=0.3.
- Exponentialfördelning (λ > 0): f(x) = λ e^{−λ x} för x ≥ 0, annars 0. Används ofta för modellering av väntetider.
- Normalfördelning N(μ, σ^2): f(x) = (1/(σ√(2π))) exp(−(x−μ)^2/(2σ^2)). Normalfördelningen är central i statistik och sannolikhetsteori.
Transformationer och förändring av variabel
Om Y = g(X) där g är en monotont växande eller avtagande funktion, kan PDF för Y hittas genom förändring av variabel:
f_Y(y) = f_X(g^{-1}(y)) · |d/dy g^{-1}(y)|.
Ett enkelt fall: om Y = aX + b (a ≠ 0) blir f_Y(y) = (1/|a|) f_X((y − b)/a).
Flerdimensionella fall: täthet för vektorer
För slumpvariabler (X, Y) definieras en gemensam täthetsfunktion f_{X,Y}(x,y) så att P((X,Y) ∈ A) = ∬_A f_{X,Y}(x,y) dx dy. Marginaltätheter erhålls genom integration, t.ex.
f_X(x) = ∫_{-∞}^{∞} f_{X,Y}(x,y) dy.
Oberoende variabler uppfyller f_{X,Y}(x,y) = f_X(x) f_Y(y).
Användningsområden
- Beräkna sannolikheter för intervall och händelser.
- Bestämma väntevärden och spridning (varians, standardavvikelse).
- Modellering av mätfel, naturliga fenomen och köteori.
- I statistisk inferens ingår PDF i sannolikhetsfunktionen (likelihood) vid parameterestimation.
Skillnad mellan PDF och PMF
För diskreta slumpvariabler används en sannolikhetsmassfunktion (PMF) p_X(k) = P(X = k). För kontinuerliga variabler gäller istället PDF f_X(x) och sannolikheten ges av integraler över intervall; därför är P(X = x) = 0 i den kontinuerliga modellen.
Sammanfattning
Sannolikhetstäthetsfunktionen (PDF) beskriver hur sannolikheten fördelas över värden för en kontinuerlig slumpvariabel. De centrala kraven är icke-negativitet och att tätheten integrerar till 1. Genom att integrera PDF över ett intervall får man sannolikheten för att variabeln ligger i det intervallet, och PDF används också för att beräkna väntevärden, varians och andra momenter samt för att hantera transformationer och flerdimensionella fördelningar.
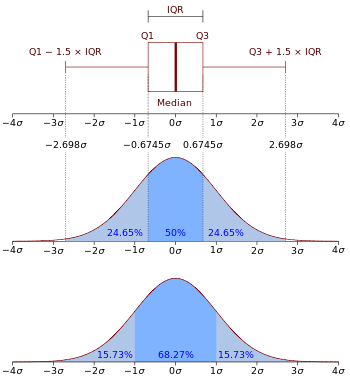
Boxplot och sannolikhetstäthetsfunktion för en normalfördelning N(0, σ2 ) .
Sannolikhetsdensitet kontra sannolikhetsmassafunktion
Sannolikhetsmassafunktionen är för en diskret sannolikhetsfördelning vad sannolikhetstäthetsfunktionen är för en kontinuerlig sannolikhetsfördelning. Sannolikhetsdensitetsfunktionen är nödvändig för att kunna arbeta med kontinuerliga fördelningar.
En slumpvariabel med en kontinuerlig sannolikhetsfördelning kan anta vilket värde som helst inom denna fördelning. Att kasta en tärning ger siffrorna 1 till 6, med en sannolikhet på 
, men detta är inte en kontinuerlig funktion, eftersom endast siffrorna 1 till 6 är möjliga.
Två personer har däremot inte samma längd eller vikt. Med hjälp av en funktion för sannolikhetstäthet är det möjligt att bestämma sannolikheten för personer mellan 180 centimeter och 181 centimeter eller mellan 80 kg och 81 kg, även om det finns oändligt många värden mellan dessa två gränser.
Relaterade sidor
- Kumulativ fördelningsfunktion
Frågor och svar
Fråga: Vad är en sannolikhetstäthetsfunktion?
S: En sannolikhetstäthetsfunktion är en funktion som karakteriserar en kontinuerlig sannolikhetsfördelning.
F: Hur skrivs sannolikhetstäthetsfunktionen för en slumpvariabel X?
S: Sannolikhetsdensitetsfunktionen för X skrivs ibland som f_X(x).
Fråga: Vad representerar integralen av sannolikhetstäthetsfunktionen?
S: Sannolikhetstäthetsfunktionens integral representerar sannolikheten för att en given slumpvariabel med given densitet ingår i ett intervall som tillhandahålls.
Fråga: Är sannolikhetstäthetsfunktionen alltid icke-negativ i hela sitt område?
S: Ja, per definition är sannolikhetsdensitetsfunktionen icke-negativ inom hela sitt område.
Fråga: Är det möjligt att integrera över ett intervall och summera till 1?
Svar: Ja, integrering över ett intervall summerar till 1.
F: Vilken typ av fördelning karakteriserar en sannolikhetstäthetsfunktion?
S: En sannolikhetsdensitetsfunktion karakteriserar alla kontinuerliga sannolikhetsfördelningar.
Sök