Vad är statistik? Definition, metoder och användningsområden
Upptäck vad statistik är: definition, centrala metoder och praktiska användningsområden inom vetenskap, medicin, ekonomi och marknadsföring — en tydlig guide för nybörjare och proffs.
Statistik är en gren av den tillämpade matematiken som handlar om att samla in, organisera, analysera, läsa och presentera data. Beskrivande statistik gör sammanfattningar av uppgifter. Med hjälp av inferentiell statistik kan man göra förutsägelser. Statistik hjälper till vid studier av många andra områden, t.ex. vetenskap, medicin, ekonomi, psykologi, politik och marknadsföring. En person som arbetar med statistik kallas statistiker. Förutom att vara namnet på ett studieområde kan ordet "statistik" också betyda siffror som används för att beskriva data eller samband.
Grundläggande begrepp
- Population – den fullständiga mängden individer eller enheter som intresserar oss (t.ex. alla röstberättigade i ett land).
- Stickprov – en delmängd av populationen som undersöks för att dra slutsatser om hela populationen.
- Variabel – en egenskap som kan mätas eller kategoriseras (t.ex. ålder, kön, inkomst).
- Data – insamlade observationer eller mätvärden, antingen kvantitativa (tal) eller kvalitativa (kategorier).
Metoder inom statistik
Statistik delas ofta in i två huvudgrupper:
- Beskrivande statistik – metoder för att sammanfatta och presentera data, t.ex. medelvärde, median, typvärde, varians, standardavvikelse och diagram (staplar, histogram, lådagram).
- Inferentiell statistik – metoder för att dra slutsatser om en population utifrån ett stickprov, t.ex. hypotesprövning, konfidensintervall och regressionsanalys.
Vanliga mått och tekniker
- Centralmått: medelvärde (genomsnitt), median (mittenvärde), och typvärde (mest frekventa värdet).
- Spridningsmått: varians, standardavvikelse och interkvartilavstånd som beskriver hur utspridda värdena är.
- Korrelations- och regressionsanalyser: undersöker samband mellan variabler och kan användas för att modellera och förutsäga resultat.
- Hypotesprövningar: metoder för att avgöra om observerade skillnader eller samband kan förklaras av slumpen.
- Bayesianska metoder: använder sannolikheter för att uppdatera kunskap baserat på ny data.
Steg i en statistisk undersökning
- Formulera frågeställning eller hypotes.
- Välja population och stickprovsmetod (slumpmässigt urval, stratifierat urval, klusterurval etc.).
- Samla in data på ett systematiskt sätt (enkäter, mätningar, observationer, registerdata).
- Bearbeta och rengöra data (hantera saknad information, felaktiga värden).
- Använda lämpliga statistiska metoder och visualiseringar.
- Tolka resultaten med hänsyn till osäkerhet och möjliga felkällor.
- Rapportera slutsatser och, vid behov, rekommendationer eller beslut.
Sannolikhetsurval, bias och felkällor
För att slutsatser från ett stickprov ska vara tillförlitliga behöver urvalet vara representativt. Vanliga problem är:
- Urvals-bias – när stickprovet inte representerar populationen (t.ex. självorienterade enkäter).
- Observer- eller mätfel – fel i insamlingen av data.
- Konfunderande variabler – dolda faktorer som påverkar sambandet mellan två variabler.
- Slumpmässigt fel – ofrånkomlig osäkerhet som minskar med större stickprov.
Visualisering och programvara
Att visa data i diagram gör det enklare att förstå mönster och avvikelser. Vanliga verktyg och program för statistisk analys och visualisering inkluderar R, Python (pandas, matplotlib, seaborn), SPSS, SAS och Excel. Väl valda diagram (t.ex. linjediagram för tidsserier, stapeldiagram för kategorier, lådagram för spridning) underlättar tolkning.
Tillämpningar och exempel
Statistik används i praktiken överallt där data ska tolkas:
- Inom vetenskap för att testa teorier och analysera experiment.
- Inom medicin för att bedöma läkemedels effekt och risker.
- Inom ekonomi för prognoser och policyeffekter.
- Inom marknadsföring för att förstå kundbeteenden och kampanjers effekt.
Etik och tolkning
Statistik kan lätt missförstås eller missbrukas. Det är viktigt att:
- Redovisa osäkerhet (t.ex. konfidensintervall) och inte bara punktuppskattningar.
- Var transparent med datainsamling, urvalsmetod och eventuella antaganden.
- Undvika att påstå kausalitet när endast korrelation har visats.
Sammanfattningsvis är statistik ett kraftfullt verktyg för att omvandla data till kunskap. Rätt använd kan den ge välgrundade insikter och stödja beslut inom många områden, men den kräver noggrann metodik och kritisk tolkning.
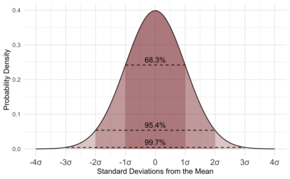
Normalfördelningen i statistiken
Historia
Den första kända statistiken är folkräkningsuppgifter. Babylonierna gjorde en folkräkning omkring 3500 f.Kr., egyptierna omkring 2500 f.Kr. och de gamla kineserna omkring 1000 f.Kr.
Från och med 1500-talet utvecklade matematiker som Gerolamo Cardano sannolikhetsteorin, vilket gjorde statistiken till en vetenskap. Sedan dess har människor samlat in och studerat statistik om många saker. Träd, sjöstjärnor, stjärnor, stenar, ord, nästan allt som kan räknas har varit föremål för statistik.
Insamling av uppgifter
Innan vi kan beskriva världen med hjälp av statistik måste vi samla in data. De uppgifter som vi samlar in i statistiken kallas mätningar. När vi har samlat in data använder vi ett eller flera siffror för att beskriva varje observation eller mätning. Anta till exempel att vi vill ta reda på hur populärt ett visst tv-program är. Vi kan välja ut en grupp människor (ett så kallat urval) ur den totala populationen av tittare. Sedan frågar vi varje tittare i urvalet hur ofta de tittar på programmet. Urvalet är uppgifter som man kan se, och populationen är uppgifter som man inte kan se (om man antar att inte alla tittare i populationen tillfrågas). Ett annat exempel: Om vi vill veta om ett visst läkemedel kan hjälpa till att sänka blodtrycket kan vi ge läkemedlet till människor under en viss tid och mäta deras blodtryck före och efter.
Beskrivande och inferentiell statistik
Siffror som beskriver de data som man kan se kallas deskriptiv statistik. Siffror som gör förutsägelser om data som man inte kan se kallas inferentialstatistik.
Beskrivande statistik innebär att man använder siffror för att beskriva egenskaper hos data. Till exempel är genomsnittslängden för kvinnor i USA en deskriptiv statistik: den beskriver en egenskap (genomsnittslängden) hos en population (kvinnor i USA).
När resultaten har sammanfattats och beskrivits kan de användas för prognoser. Detta kallas inferentialstatistik. Som exempel kan nämnas att storleken på ett djur beror på många faktorer. Vissa av dessa faktorer kontrolleras av miljön, men andra är ärftliga. En biolog skulle därför kunna göra en modell som säger att det finns en hög sannolikhet för att avkomman kommer att vara liten i storlek - om föräldrarna var små i storlek. Denna modell gör det förmodligen möjligt att förutsäga storleken på ett bättre sätt än genom att bara gissa slumpmässigt. Att testa om ett visst läkemedel kan användas för att bota ett visst tillstånd eller en viss sjukdom görs vanligen genom att jämföra resultaten från personer som får läkemedlet med dem som får placebo.
Metoder
Oftast samlar vi in statistiska uppgifter genom att göra undersökningar eller experiment. En opinionsundersökning är till exempel en typ av undersökning. Vi väljer ut ett litet antal personer och ställer frågor till dem. Sedan använder vi deras svar som data.
Valet av vilka personer som ska delta i en undersökning eller datainsamling är viktigt eftersom det direkt påverkar statistiken. När statistiken är klar kan man inte längre avgöra vilka individer som tagits med. Anta att vi vill mäta vattenkvaliteten i en stor sjö. Om vi tar prover bredvid avloppet kommer vi att få andra resultat än om proverna tas på en avlägsen och svårtillgänglig plats i sjön.
Det finns två typer av problem som ofta uppstår vid provtagning:
- Om det finns många stickprov, kommer stickproven sannolikt att ligga mycket nära den verkliga populationen. Om det däremot finns väldigt få prov kan de skilja sig mycket från vad de är i den verkliga populationen. Detta fel kallas slumpfel (se även Fel och residualer i statistik).
- De personer som ingår i proverna måste väljas med omsorg. Vanligtvis väljs de slumpmässigt. Om så inte är fallet kan urvalet vara mycket annorlunda än vad det verkligen är i den totala populationen. Detta gäller även om ett stort antal stickprov tas. Denna typ av fel kallas bias.
Fel
Vi kan minska slumpmässiga fel genom att ta ett större urval, och vi kan undvika en viss bias genom att välja slumpmässigt. Ibland är det dock svårt att ta stora slumpmässiga urval. Och snedvridning kan uppstå om olika personer inte tillfrågas eller vägrar att svara på våra frågor, eller om de vet att de får en falsk behandling. Dessa problem kan vara svåra att åtgärda. Se standardfel för mer information.
Beskrivande statistik
Att hitta mitten av uppgifterna
Mittpunkten av uppgifterna kallas medelvärde. Genomsnittet berättar om en typisk individ i populationen. Det finns tre typer av medelvärden som ofta används: medelvärdet, medianen och modus.
I exemplen nedan används dessa exempeluppgifter:
| Namn | A | B | C | D | E | F | G | H | I | J |
| Poäng | 23 | 26 | 49 | 49 | 57 | 64 | 66 | 78 | 82 | 92 |
Medelvärde
Formeln för medelvärdet är
Där 

Detta innebär att man beräknar medelvärdet genom att addera alla värden och sedan dividera med antalet värden. I exemplet ovan är medelvärdet:
Problemet med medelvärdet är att det inte säger något om hur värdena är fördelade. Värden som är mycket stora eller mycket små ändrar medelvärdet mycket. I statistiken kan dessa extremvärden vara mätfel, men ibland innehåller populationen verkligen dessa värden. Om det till exempel finns 10 personer i ett rum som tjänar 10 dollar per dag och 1 som tjänar 1 000 000 dollar per dag. Medelvärdet av uppgifterna är 90 918 dollar per dag. Även om det är det genomsnittliga beloppet är medelvärdet i det här fallet inte det belopp som en enskild person tjänar, och är därför inte särskilt användbart för vissa ändamål.
Det medelvärde som beskrivs ovan är det "aritmetiska medelvärdet". Andra typer är användbara för vissa ändamål.
Median
Medianen är den mellersta posten i uppgifterna. För en given data 

Som ett annat exempel, som liknar inkomstexemplet som presenterades för medelvärdet, kan man tänka sig ett rum med 10 personer som har inkomster på 10, 20, 20, 20, 40, 50, 60, 90, 90, 90, 100 och 1 000 000 dollar. Här är medianen 55 dollar, eftersom 55 dollar är medelvärdet av de två mittersta siffrorna, 50 dollar och 60 dollar. Om man bortser från extremvärdet 1 000 000 dollar blir medianen 53 dollar. I detta fall ligger medianen nära det värde som erhålls när extremvärdet kastas bort. Medianen löser problemet med extremvärden som beskrivs i definitionen av medelvärde ovan.
Läge
Läget är den mest frekventa uppgiften. Den vanligaste bokstaven på engelska är till exempel bokstaven "e". Vi skulle säga att "e" är modus i fördelningen av bokstäverna.
Ett annat exempel: Om det finns 10 personer i ett rum med inkomster på 10, 20, 20, 20, 40, 50, 60, 90, 90, 90, 90, 90, 100 och 1 000 000 dollar är modusvärdet 90 dollar, eftersom 90 dollar förekommer tre gånger och alla andra värden förekommer färre än tre gånger.
Det kan finnas mer än ett läge. Om det till exempel finns tio personer i ett rum med inkomster på 10, 20, 20, 20, 20, 20, 50, 60, 90, 90, 90, 90, 90, 100 och 1 000 000 dollar är lägena 20 och 90 dollar. Detta är bi-modalt, eller har två modaliteter. Bi-modalitet är mycket vanligt och indikerar ofta att data är en kombination av två olika grupper. Till exempel har den genomsnittliga längden för alla vuxna i USA en bipmodal fördelning. Detta beror på att män och kvinnor har separata genomsnittslängder på 1,763 m (5 ft 9 + 1⁄2 in) för män och 1,622 m (5 ft 4 in) för kvinnor. Dessa toppar är tydliga när båda grupperna kombineras.
Modus är den enda form av medelvärde som kan användas för data som inte kan ordnas.
Hitta spridningen av uppgifterna
En annan sak som vi kan säga om en uppsättning data är hur utspridda de är. Ett vanligt sätt att beskriva spridningen av en uppsättning data är standardavvikelsen. Om standardavvikelsen för en uppsättning data är liten ligger de flesta data mycket nära genomsnittet. Om standardavvikelsen däremot är stor är en stor del av uppgifterna mycket annorlunda än genomsnittet.
Standardavvikelsen för ett urval skiljer sig i allmänhet från standardavvikelsen för den ursprungliga populationen . Därför skriver vi 

Om data följer ett vanligt mönster som kallas normalfördelning är det mycket användbart att känna till standardavvikelsen. Om uppgifterna följer detta mönster (vi skulle säga att uppgifterna är normalfördelade) kommer ungefär 68 av 100 uppgifter att avvika från genomsnittet med mindre än standardavvikelsen. Inte bara det, utan ungefär 95 av 100 mätningar kommer att avvika från genomsnittet med mindre än två gånger standardavvikelsen, och ungefär 997 av 1000 kommer att ligga närmare genomsnittet med mindre än tre standardavvikelser.
Annan beskrivande statistik
Vi kan också använda statistik för att ta reda på att en viss procent, percentil, antal eller bråkdel av människor eller saker i en grupp gör något eller passar in i en viss kategori.
Samhällsvetare använde till exempel statistik för att ta reda på att 49 procent av världens människor är män.
Relaterad programvara
För att stödja statistiker har många statistiska program utvecklats:
- MATLAB
- R
- SAS Institute
- SPSS (tillverkad av IBM)
Frågor och svar
F: Vad är statistik?
S: Statistik är en gren av tillämpad matematik som handlar om att samla in, organisera, analysera, läsa och presentera data.
F: Vilka är de två typerna av statistik?
S: De två typerna av statistik är deskriptiv och inferentiell statistik. Beskrivande statistik gör sammanfattningar av data medan inferentiell statistik gör förutsägelser.
F: Hur hjälper statistiken inom andra områden?
S: Statistik hjälper till vid studier av många andra områden, t.ex. vetenskap, medicin, ekonomi, psykologi, politik och marknadsföring.
F: Vem arbetar med statistik?
S: En person som arbetar med statistik kallas statistiker.
F: Vad betyder ordet "statistik"?
S: Förutom att vara namnet på ett studieområde kan ordet "statistik" också betyda siffror som används för att beskriva data eller samband.
F: Vilka aktiviteter ägnar sig statistiker åt?
S: Statistiker ägnar sig åt aktiviteter som att samla in, organisera, analysera, läsa och presentera data.
Sök

