Linjär regression: definition, multipel modell och minsta kvadratmetoden

Lär dig linjär regression: definition, multipel modell och minsta kvadratmetoden för prediktion, tolkning och modellval — tydliga förklaringar och praktiska exempel.

Författare: Leandro Alegsa

Linjär regression är en metod för att beskriva och kvantifiera samband mellan en beroende variabel (ofta betecknad y) och en eller flera förklarande variabler (ofta betecknade X, X1, X2 …). I sin enklaste form, enkel linjär regression med en förklarande variabel, modelleras sambandet som

y = β0 + β1 x + ε,

där β0 är interceptet, β1 är lutningen (effekten av x på y) och ε är ett slumpmässigt fel (residual). Den räta linje som beskriver modellen kallas regressionslinje.

Användningsområden

  • Prediktion: Linjär regression kan användas för att anpassa en prediktiv modell till observerade data. När en modell är uppskattad kan den användas för att förutsäga y för nya värden av X. Den predicerade (skattade) y betecknas ofta  ŷ; i originalexemplet illustreras detta med följande bild: {\displaystyle {\hat {y}}}
  • Orsakssamband och tolkning: Med en beroende variabel y och flera förklarande variabler X1, …, Xp kan linjär regressionsanalys kvantifiera styrkan i sambandet mellan y och varje Xj, testa om enskilda effekter är signifikanta och identifiera vilka variabler som tillför information respektive vilka som är överflödiga.

Multipel linjär regression (multipel modell)

I multipel regression används flera förklarande variabler. I matrisform skrivs modellen ofta som

y = Xβ + ε,

där X är designmatrisen (med en kolumn av ettor om en intercept ingår), β är vektorn av okända koefficienter och ε är feltermen. Varje komponent i β tolkas som den förväntade förändringen i y när motsvarande Xj ökar med en enhet, givet att övriga förklarande variabler hålls konstanta.

Minsta kvadratmetoden (estimering)

En vanlig metod för att uppskatta koefficienterna är minsta kvadrat-metoden (ofta kallad ordinary least squares, OLS). Metoden väljer de koefficienter som minimerar summan av kvadraterna av residualerna (vertikala avstånd mellan observerade och förväntade värden). För multipla linjära modeller ger detta en sluten formel för skattning (i matrisnotation):

β̂ = (X'X)-1X' y

Under vissa antaganden (se nedan) har OLS-estimaten goda egenskaper: de är linjära, obiaserade och har minst varians bland alla linjära obiaserade estimatorer (Gauss–Markov-teoremet), det vill säga BLUE (Best Linear Unbiased Estimator).

Antaganden

De vanligaste grundantagandena för klassisk linjär regression är:

  • Linjäritet: Sambandet mellan förklarande variabler och den förväntade värdet av y är linjärt i parametrarna.
  • Oberoende: Observationerna (eller feltermerna) är oberoende.
  • Homoskedasticitet: Variansen i feltermerna är konstant för alla nivåer av förklarande variabler.
  • Ingen perfekt multikollinearitet: Ingen förklarande variabel är en exakt linjärkombination av andra.
  • Normalitet (vid inferens): Feltermerna är normalt fördelade om man vill göra exakta konfidensintervall och hypotesprövningar för små provstorlekar.

Modellutvärdering och diagnostik

Efter att modellen har anpassats är det viktigt att kontrollera om antagandena håller:

  • Residualplot: Plottar residualer mot förutsagda värden eller mot varje förklarande variabel för att upptäcka mönster eller heteroskedasticitet.
  • Normalitetskontroll: Q–Q-plot eller tester (t.ex. Shapiro–Wilk) för att bedöma om residualerna är nära normalfördelade.
  • Influens och outliers: Mätetal som Cook’s distance, leverage och DFBETAS används för att upptäcka observationer som påverkar skattningarna kraftigt.
  • Multikollinearitet: Variance Inflation Factor (VIF) hjälper att identifiera stark korrelation mellan förklarande variabler.
  • Heteroskedasticitetstest: T.ex. Breusch–Pagan-test för att testa om variansen i residualerna är konstant.

Mått på förklaringsgrad och modellval

Vanliga mått för att bedöma modellens förklaringskraft är R2 och justerat R2. För att jämföra modeller med olika antal parametrar används även kriterier som AIC och BIC eller korsvalidering. Vid variabelurval tillämpas metoder som stegvist urval, LASSO eller regelbundna urvalsmetoder baserade på korsvalidering.

Alternativ och varianter

Det finns flera varianter och alternativa metoder när klassiska antaganden bryts eller när olika mål eftersträvas:

  • Robusta metoder (t.ex. regression med minsta absoluta avvikelser) minskar känsligheten för outliers.
  • Strukturering med straff (regularisering): Ridge-regression och LASSO lägger till strafftermer för att hantera multikollinearitet och förbättra prediktionsegenskaper.
  • Generaliserade linjära modeller (GLM) för icke-normal respons (t.ex. logistisk regression för binär respons).
  • Ikke-linjära modeller och icke-parametriska metoder när sambandet inte är linjärt i parametrarna.

Praktiska råd

  • Skala och centra kontinuerliga förklarande variabler före tolkning eller regularisering—det förenklar tolkningen av koefficienter och numerisk stabilitet.
  • Inkludera bara meningsfulla interaktioner och polynomled när det finns teoretiska skäl eller empirisk evidens.
  • Använd korsvalidering för att bedöma modellens prediktiva prestanda på nya data.
  • Tänk på syftet: om målet är prediktion kan man prioritera metoder som optimerar förutsägbarhet; om målet är begriplig tolkning bör man fokusera på modeller med tydlig parameterinterpretation.

Sammanfattning

Linjär regression är ett grundläggande och flexibelt verktyg för både prediktion och statistisk inferens. Även om modellen är enkel — en räta linje i det tvådimensionella fallet eller en linjär kombination i multipla fall — kräver korrekt användning att man kontrollerar antaganden, bedömer modellkvalitet och överväger alternativa metoder när antaganden bryts. Linjär regression och regressionsanalyser i allmänhet utgör grundpelare i statistisk analys tack vare sin tydlighet, tolkbarhet och välkända matematiska egenskaper.

Observera att termerna "minsta kvadrat" och "linjär modell" ofta används tillsammans men inte är synonyma: minsta kvadrat-principen kan också appliceras på vissa icke-linjära modeller, och linjära modeller kan anpassas med andra förlustfunktioner (t.ex. minsta absoluta avvikelser eller penaliserade varianter som ridge-regression). För mer avancerade val av normer och förlustfunktioner se även diskussioner om olika normer och anpassningsmetoder.

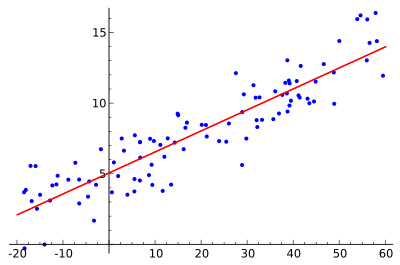
Tanken är att hitta den röda kurvan, de blå punkterna är faktiska prov. Med linjär regression kan alla punkter kopplas samman med hjälp av en enda rak linje. I det här exemplet används enkel linjär regression, där kvadraten på avståndet mellan den röda linjen och varje provpunkt minimeras.  Zoom
Tanken är att hitta den röda kurvan, de blå punkterna är faktiska prov. Med linjär regression kan alla punkter kopplas samman med hjälp av en enda rak linje. I det här exemplet används enkel linjär regression, där kvadraten på avståndet mellan den röda linjen och varje provpunkt minimeras.  

Användning

Ekonomi

Linjär regression är det viktigaste analysverktyget inom ekonomin. Det används till exempel för att gissa konsumtionsutgifter, fasta investeringar, lagerinvesteringar, inköp av ett lands exportvaror, importutgifter, efterfrågan på likvida tillgångar, efterfrågan på arbetskraft och arbetskraftsutbud.


 

Relaterade sidor



 

Frågor och svar

F: Vad är linjär regression?


S: Linjär regression är ett sätt att med hjälp av matematik undersöka hur något förändras när andra saker förändras. Den använder en beroende variabel och en eller flera förklarande variabler för att skapa en rak linje, som kallas "regressionslinje".

F: Vilka är fördelarna med linjär regression?


S: Modeller som beror linjärt på sina okända parametrar är lättare att anpassa än modeller som är icke-linjärt relaterade till sina parametrar. Dessutom är de statistiska egenskaperna hos de resulterande estimatorerna lättare att fastställa.

F: Vilka är några praktiska användningsområden för linjär regression?


S: Linjär regression kan användas för att anpassa en prediktiv modell till observerade värden (data) för att göra förutsägelser, prognoser eller reduktioner. Den kan också användas för att kvantifiera styrkan i sambanden mellan variabler och identifiera delmängder av data som innehåller överflödig information om en annan variabel.

F: Hur försöker linjära regressionsmodeller minimera fel?


S: Linjära regressionsmodeller försöker göra det vertikala avståndet mellan linjen och datapunkterna (residualerna) så litet som möjligt. Detta görs genom att minimera antingen summan av residualernas kvadrater (minsta kvadraterna), bristande anpassning i någon annan norm (minsta absoluta avvikelser) eller genom att minimera en straffad version av förlustfunktionen för minsta kvadraterna (ridge-regression).

F: Är det möjligt att modeller för linjär regression inte baseras på minsta kvadrat?


S: Ja, det är möjligt att modeller för linjär regression inte baseras på minsta kvadratmetoden utan i stället använda metoder som att minimera bristande anpassning i någon annan norm (minsta absoluta avvikelser) eller att minimera en straffad version av minsta kvadraternas förlustfunktion (ridge regression).

F: Är "linjär modell" och "minsta kvadrat" synonymer?


Svar: Nej, de är inte synonymer. Även om de är nära sammankopplade avser "linjär modell" specifikt att använda en rak linje medan "minsta kvadrat" specifikt avser att försöka minimera fel genom att se till att det finns ett minimalt vertikalt avstånd mellan linjen och datapunkterna.


Sök
AlegsaOnline.com - 2020 / 2025 - License CC3