Newtons tre rörelselagar – Förklaring och betydelse inom klassisk mekanik
Förklara Newtons tre rörelselagar: tydlig genomgång, konkreta exempel och deras betydelse inom klassisk mekanik för både vardag och vetenskap.
Isaac Newton (1642-1727) är allmänt känd som dynamikens fader, läran om rörelse. Han utvecklade tre lagar som utgör grunden för den klassiska mekaniken. Man tror att de är sanna eftersom resultaten av forskarnas experiment stämmer överens med hans lagar.
Newtons tre rörelselagar — översikt
Newtons tre lagar beskriver hur föremål rör sig under inverkan av krafter. Tillsammans med begrepp som kraft, massa och acceleration ger de en enkel men mycket användbar modell för mekaniska system på vardagliga skalor och i astronomi. Lagarna gäller i den klassiska (icke-relativistiska) ramen och när kvantmekaniska effekter kan försummas.
Första lagen — tröghetslagen
Första lagen säger i korthet att ett föremål fortsätter i samma rörelsetillstånd (vila eller konstant hastighet i en rak linje) så länge ingen nettokraft verkar på det. Detta är ofta kallat tröghetslagen.
- Om nettokraften är noll: rörelsehastigheten är konstant.
- Detta kräver ett inertialsystem (ett referenssystem som inte accelererar). I ett roterande eller accelererande system uppträder till synes "fiktiva" krafter (t.ex. centrifugalkraft, Corioliskraft).
- Exempel: en bok på ett bord ligger stilla tills någon skjuter den — friktion och normalkraft är krafter som avgör om boken rör sig eller inte.
Andra lagen — kraft = massa × acceleration
Andra lagen kvantifierar sambandet mellan kraft, massa och acceleration. Den uttrycks vanligen som F = m · a, där F är nettokraften (vektor), m massan (skalär) och a accelerationen (vektor).
- Formeln är vektorform: riktningen på accelerationen är samma som nettokraftens riktning.
- Enheten för kraft i SI-systemet är newton (N), där 1 N = 1 kg·m/s².
- Massan i klassisk mekanik betraktas som konstant (vilket ändras i relativistiska sammanhang).
- Praktiska exempel: bromssträcka för en bil, beräkning av dragkraft för en raket, eller tyngden hos ett föremål (tyngd = massa × gravitationsacceleration).
Tredje lagen — kraftpar och verkan-reaktion
Tredje lagen lyder att för varje kraft som ett föremål A utövar på ett föremål B finns en lika stor men motsatt riktad kraft som B utövar på A. Detta uttrycks ofta som "verkan och reaktion".
- Krafterna verkar på olika kroppar — därför tar de inte ut varandra i ett enda objekt.
- Denna lag leder direkt till rörelsemängdens bevarande i slutna system: inga yttre krafter → total rörelsemängd konstant.
- Exempel: när du trycker handen mot en vägg upplever du en lika stor motkraft från väggen; raketens uppdriv kommer av gaser som kastas bakåt och reaktionen skjuter raketen framåt.
Viktiga begrepp och praktiska aspekter
- Inertialsystem: Newtons lagar gäller direkt i inertialsystem. I ett accelererat referenssystem måste man införa fiktiva krafter för att använda samma formulering.
- Vektornatur: Kraft och acceleration är vektorer — deras riktning är avgörande för resultatet.
- Rörelsemängd: rörelsemängden p = m·v och dess tidsderivata dp/dt är lika med netto-kraften; detta kopplar Newtons andra lag till bevarandeprinciper.
- Gravitation i Newtons modell: Newtons universella gravitationslag beskriver tyngdkraften som en kraft mellan massor och användes framgångsrikt för att förutsäga planeters banor.
Begränsningar och när Newtons lagar inte räcker
- Relativistiska hastigheter: nära ljusets hastighet krävs Einsteins relativitetsteori. Då används fyravektorer och den klassiska formen F = m·a bryter ner.
- Kvantmekanik: på atomär och subatomär skala beskrivs partiklar inte längre med klassiska banor, utan med sannolikhetsvågor och kvantoperatorer.
- Icke-inertiala referenssystem: i roterande system uppträder pseudokrafter som måste beaktas.
Historisk betydelse och tillämpningar
Newton formulerade sina lagar i verket "Philosophiæ Naturalis Principia Mathematica" (1687). De lade grunden för klassisk mekanik och gjorde det möjligt att matematiskt förutsäga rörelse för allt från fallande äpplen till planeters banor. I praktiken används Newtons lagar fortfarande i de flesta ingenjörstillämpningar, konstruktioner, fordonsteknik, robotik och rymdnavigation, så länge relativistiska och kvantmekaniska effekter är försumbara.
Vanliga missförstånd
- Att "ingen kraft innebär rörelsefrihet" — korrekt är att ingen nettokraft innebär oförändrad rörelsetillstånd; ett föremål i rörelse fortsätter framåt med konstant hastighet om ingen nettokraft verkar.
- Att tredje lagen skulle "ta ut" krafter i ett enda objekt — de agerar på olika kroppar och kan därför inte enkelt summeras bort för en enskild kropp.
Sammanfattning
Newtons tre rörelselagar ger en enkel, kraftfull och ofta tillräcklig modell för att beskriva och förutsäga mekaniska rörelser i många praktiska sammanhang. De förklarar hur krafter orsakar acceleration, hur tröghet fungerar och hur krafter alltid uppträder i par. Trots sina begränsningar i extrema förhållanden är de fortfarande fundamentala inom teknik och vetenskap.

Originalpublikation av de två första lagarna, på latin.
Första lagen
- Om en kropp är i vila förblir den i vila eller, om den är i rörelse, rör den sig med jämn hastighet tills den påverkas av en nettokraft.
En "jämn hastighet" innebär att ett föremål rör sig med en konstant hastighet utan att ändra riktning (dvs. i en rak linje). En "nettokraft" innebär att de krafter som verkar på föremålet inte är balanserade. Med andra ord säger den första lagen två saker:
- Ett stillastående föremål rör sig bara om det finns en obalanserad kraft som verkar på det.
- Ett rörligt föremål ändrar bara hastighet eller riktning om det finns en obalanserad kraft som verkar på det.
I den första delen sägs att ett bord som står på marken inte rör sig om det inte knuffas. Även om gravitationen verkar på bordet och drar det nedåt, finns det en reaktionskraft från marken som trycker tillbaka det. De krafter som verkar på bordet är balanserade, så föremålet kommer inte att röra sig.
Den andra delen är svårare att förstå. En boll som rullar längs en plan yta kommer att sakta ner och till slut stanna upp. Men detta beror på friktion, som är en kraft som bromsar bollen. En boll som rullar nedför en sluttning påverkas också av friktion, men gravitationskraften som får den att röra sig är starkare. På en plats utan friktionskrafter, luftmotstånd och gravitation (t.ex. i rymden) skulle ett rörligt föremål fortsätta att röra sig i en rak linje om det inte fanns någon kraft som bromsade upp det eller ändrade dess riktning.
Andra lagen
- För en partikel med massan m är nettokraften F på partikeln lika med massan m gånger partikelns acceleration a:
F = m a {\displaystyle \mathbf {F} =m\mathbf {a} } 
Newtons andra lag säger att en partikels acceleration är beroende av de krafter som verkar på partikeln och partikelns massa. För en given partikel ökar accelerationen om nettokraften ökar. För en given nettokraft gäller att ju mer massa en partikel har, desto mindre acceleration har den.
Till exempel är vikt en kraft som vi känner på jorden och som orsakas av gravitationen. Vikten W på en partikel ges av följande
W = m g {\displaystyle \mathbf {W} =m\mathbf {g} } 
där m är partikelns massa och g är den lokala gravitationsaccelerationen (inte att förväxla med G, den universella gravitationskonstanten), som ungefär motsvarar 9,8 meter per sekund2 (32 fot per sekund2 ) på jorden.
Vi kan uttrycka Newtons andra lag i termer av rörelsemängd. En partikel har en impuls p som definieras som produkten av dess massa m och hastighet v:
p = m v {\displaystyle \mathbf {p} =m\mathbf {v} } 
Accelerationen a för en partikel är tidsderivatan av dess hastighet v:
a = d v d t {\displaystyle \mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}}}
Därför,
F = m a = m d v d t = d ( m v ) d t = d p d t {\displaystyle \mathbf {F} =m\mathbf {a} =m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} (m\mathbf {v} )}{\mathrm {d} t}}={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d}}}}}}
Vi har alltså ett annat sätt att uttrycka Newtons andra lag:
- För en partikel med massan m är nettokraften F på partikeln lika med tidsderivatan av partikelns rörelsemängd p:
F = d p d t {\displaystyle \mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}}}}
I den klassiska mekaniken finns de två formerna av den andra lagen, F = m a {\displaystyle \mathbf {F} =m\mathbf {a} }

Tredje lagen
- För varje handling finns det en lika stor och motsatt reaktion. Eller så reagerar varje handling alltid i motsatt riktning.
Detta kan bäst förstås med biljardkulor, där man lätt kan se hur kraftparen verkar och reagerar. När du sparkar en fotboll rör sig inte bara bollen utan du känner också en kraft på din fot.
Storleken på krafterna på det första föremålet är lika stor som storleken på kraften på det andra föremålet. Kraftriktningen på det första föremålet är motsatt till kraftriktningen på det andra föremålet. Krafter finns alltid i par - lika och motsatta kraftpar med verkan och reaktion.
I naturen förekommer en mängd olika aktions-reaktionskraftpar. Tänk på en fisks framdrivning genom vattnet. Fisken använder sina fenor för att trycka vattnet bakåt. Men en knuff mot vattnet kommer bara att tjäna till att accelerera vattnet. Eftersom krafter är resultatet av ömsesidiga interaktioner måste vattnet också trycka fisken framåt och driva fisken genom vattnet. Storleken på kraften på vattnet är lika stor som storleken på kraften på fisken; riktningen på kraften på vattnet (bakåt) är motsatt riktningen på kraften på fisken (framåt). För varje handling finns det en lika stor (i storlek) och motsatt (i riktning) reaktionskraft. Aktion-reaktionskraftpar gör det möjligt för fiskar att simma.
Tänk på en bils rörelse på väg till skolan. En bil har hjul som snurrar framåt. När hjulen snurrar framåt griper de tag i vägen och pressar vägen bakåt. Eftersom krafter är resultatet av ömsesidiga interaktioner måste vägen också trycka på hjulen framåt. Storleken på kraften på vägen är lika stor som storleken på kraften på hjulen (eller bilen); riktningen på kraften på vägen (bakåt) är motsatt riktningen på kraften på hjulen (framåt). För varje handling finns det en lika stor (i storlek) och motsatt (i riktning) reaktion. Aktion-reaktionskraftpar gör det möjligt för bilar att röra sig längs en vägbana.
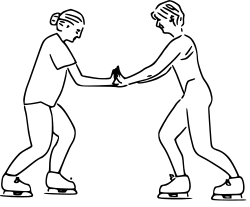
Newtons tredje lag. Skridskoåkarnas krafter på varandra är lika stora och verkar i motsatt riktning.
Relaterade sidor
- Philosophiæ Naturalis Principia Mathematica
- Klassisk mekanik
Sök