Lavineffekt (lavinverkan) – definition inom kryptografi
Lavineffekt (lavinverkan) i kryptografi: hur små förändringar i indata sprider sig i blockchiffer och hashfunktioner för stark kryptering och bättre säkerhet.
Lavineffekten (på engelska ofta kallad "avalanche effect", på svenska ibland "lavinverkan") är en önskvärd egenskap hos algoritmer för blockchiffer och kryptografiska hashfunktioner. Effekten innebär att en liten förändring i ingången (t.ex. att en enda bit vänds) leder till att en stor och till synes slumpmässig del av resultatet ändras. I väldesignade blockchiffer betyder det att en liten förändring i antingen nyckeln eller klartexten bör orsaka en kraftig och oförutsägbar förändring i chiffertexten, så att varje bit i utdata påverkas av många bitar i indata.
Varför lavineffekt är viktigt
Lavineffekten bidrar till god Shannons förvirringsegenskap och diffusion: utan tillräcklig lavinverkan finns kvarstående korrelationer mellan indata och utdata som en kryptoanalytiker kan utnyttja för att göra prognoser om inmatningen endast utifrån utmatningen. Bristande lavinverkan innebär alltså dålig randomisering och kan vara tillräckligt för att helt eller delvis knäcka algoritmen med tekniker som differential- eller linjär kryptoanalys.
Formella kriterier och mätning
En formell och ofta använd måttstock är det så kallade Strict Avalanche Criterion (SAC): om enbart en ingångsbit inverteras, ska varje utgångsbit förändras med sannolikheten 0,5 (50 %). Praktiskt mäts lavineffekt genom att systematiskt invertera enskilda bitar i indata, köra algoritmen och räkna andelen utbitsändringar. Ett relaterat begrepp är Bit Independence Criterion (BIC) som kräver att förändringar i olika utgångsbitar uppför sig oberoende av varandra när en ingångsbit ändras.
Designprinciper som ger lavinverkan
För att uppnå stark lavinverkan använder kryptografiska konstruktioner flera etablerade tekniker:
- Produktchiffer (exempelvis Feistel-nätverk och substitutions-permutationsnätverk) kombinerar flera omgångar av icke-linjära komponenter och permutationer så att små förändringar sprids snabbt över hela blocket.
- Substitutionsboxer (S-boxar) och icke-linjära transformationer bryter linjära samband mellan in- och utdata.
- Diffusionslager (t.ex. MixColumns i AES eller permutationer i andra nätverk) sprider information över många bitar, så att varje utgångsbit beror på många ingångsbitar.
- Stora datablock och iterativa kompressionsfunktioner i hashfunktioner (t.ex. Merkle–Damgård- eller svampsstrukturer) hjälper till att blanda indata så att små skillnader påverkar hela hashen.
Praktiska exempel
I historiska och moderna algoritmer kan man se lavinprincipens påverkan: DES (ett Feistel-baserat chiffer) uppnår exempelvis god spridning efter flera rundor, medan moderna chiffer som AES (ett substitutions-permutationsnätverk) har inbyggda lager (ShiftRows, SubBytes, MixColumns) som snabbt ger hög diffusion. Bland hashfunktioner strävar MD5, SHA-1, SHA-2 och SHA-3 efter att en liten ändring i meddelandet ska ändra hela digesten dramatiskt; när detta inte sker i tillräcklig grad uppstår kollisionsrisker eller andra svagheter.
Testning och säkerhetskonsekvenser
Utvecklare och forskare testar lavinverkan statistiskt (t.ex. genom Monte Carlo-simuleringar eller standardiserade testsviter från NIST). Om en algoritm inte uppvisar nära 50 % sannolikhet för bitflip i genomsnitt kan det vara ett tecken på svaghet. Dessutom analyseras korrelationer och beroenden mellan utgångsbitar (BIC) för att upptäcka strukturella brister.
Sammanfattning
Lavineffekten är ett centralt krav för säkra chiffer och hashfunktioner: den säkerställer att små förändringar i indata ger stora, oförutsägbara förändringar i utdata. Detta motverkar kryptoanalytiska metoder som utnyttjar samband mellan in- och utdata och är därför ett av de viktigaste målen vid konstruktion av starka kryptografiska algoritmer. Matematiskt sett används bland annat idéer från fjärilseffekten för att beskriva hur små ändringar kan få stora följder, vilket är anledningen till att många blockchiffer är produktchiffer och att hashfunktioner ofta opererar på stora datablock.
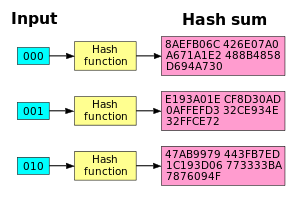
Hashfunktionen SHA1 har en bra lavinverkan. När en enda bit ändras blir hashsumman helt annorlunda.
Namn
Namnet har sitt ursprung i jordskred. En liten sten kan falla ner och tillsammans med lite snö skapa ett destruktivt jordskred. Stenen var liten, men kunde orsaka mycket förstörelse. Det är samma sak som vad denna effekt gör. En liten förändring av insatsen (stenen) bör förändra resultatet (landskapet).
Strikt kriterium för laviner
Det strikta lavinkriteriet (SAC; ett "starkt jordskredskriterium") är en egenskap hos boolska funktioner. Det är av betydelse för kryptografi. Det är uppfyllt om alla utgångsbitar förändras med en sannolikhet på 50 procent om en enda ingångsbit förändras.
SAC byggde på begreppen evolutionskompletthet och lavin. Det introducerades av Webster och Tavares 1985. Numera är det ett krav för varje modernt kryptografiskt system. Det uppfylldes t.ex. av alla finalister i AES-tävlingen.
Kriterium för bitoberoende
Kriteriet Bit independence criterion (BIC; ett kriterium som är oberoende av biten) är ett kriterium. Det lyder: När en enskild ingångsbit ändras (inverteras) ska två utgångsbitar ändras oberoende av varandra. Detta gäller för alla bitar.
Den skulle t.ex. inte vara nöjd om den ena utgångsbiten endast ändras när den andra utgångsbiten också ändras. De kanske ändras bara för att inmatningsbiten ändras. I annat fall skulle utgångsbitarna vara beroende av varandra.
Relaterade sidor
- Förvirring och spridning
Frågor och svar
Fråga: Vad är lavinverkan?
S: Lavineffekten (även känd som "jordskredseffekten") är en egenskap hos blockchiffer och algoritmer för kryptografiska hashfunktioner som säger att en liten förändring av nyckeln eller klartexten bör leda till en kraftig förändring av chiffertexten.
F: Vem använde först termen "lavinverkan"?
S: Termen lavinverkan användes för första gången av Horst Feistel 1973.
F: Hur förhåller sig detta till Shannons förvirringsegenskap?
S: Begreppet lavinverkan identifierades genom Shannons egenskap av förvirring, som anger att om ett blockchiffer eller en kryptografisk hashfunktion inte uppfyller denna grad i betydande grad, så har den dålig randomisering och kan delvis eller helt brytas (knäckas).
F: Vilka är några designmål när man skapar starka chiffer?
S: När människor skapar starka chiffer försöker de bygga in en bra lavinverkan i dem med hjälp av matematiska principer som fjärilseffekten. Detta är anledningen till att de flesta blockchiffer är produktchiffer och till att hashfunktioner har stora datablock.
F: Vad händer om en algoritm inte uppfyller lavineffekten?
S: Om en algoritm inte uppfyller avalancheeffekten i betydande grad har den dålig randomisering och kan delvis eller helt brytas (knäckas) av kryptoanalytiker som kan göra prognoser om inmatningen baserat på endast en given utmatning.
F: Varför använder de flesta blockchiffrar produktchiffrar?
S: De flesta blockchiffer använder produktchiffer eftersom de hjälper till att bygga in bra avalanceeffekter i dem med hjälp av matematiska principer som fjärilseffekten.
F: Varför har hashfunktioner stora datablock?
S: Hashfunktioner har stora datablock eftersom de hjälper till att bygga upp goda avalanceeffekter med hjälp av matematiska principer, t.ex. fjärilseffekten.
Sök