Algoritm

Jämförelse av algoritmer

Det finns oftast mer än ett sätt att lösa ett problem. Det kan finnas många olika recept för att göra en viss maträtt som ser olika ut men som till slut smakar likadant. Samma sak gäller för algoritmer. Vissa av dessa sätt kommer dock att vara bättre än andra. Om ett recept kräver många komplicerade ingredienser som du inte har är det inte lika bra som ett enkelt recept. När vi tittar på algoritmer som ett sätt att lösa problem vill vi ofta veta hur lång tid det skulle ta för en dator att lösa problemet med hjälp av en viss algoritm. När vi skriver algoritmer vill vi att vår algoritm ska ta så lite tid som möjligt så att vi kan lösa vårt problem så snabbt som möjligt.

När det gäller matlagning är vissa recept svårare att göra än andra, eftersom de tar längre tid att göra färdigt eller har fler saker att hålla reda på. Det är samma sak med algoritmer, och algoritmer är bättre när de är lättare för datorn att göra. Det som mäter svårigheten hos en algoritm kallas komplexitet. När vi frågar hur komplex en algoritm är vill vi ofta veta hur lång tid det tar för en dator att lösa det problem vi vill att den ska lösa.

Sortering

Detta är ett exempel på en algoritm för att sortera kort med färger i högar med samma färg:

1. Plocka upp alla korten.
2. Välj ett kort från din hand och titta på kortets färg.
3. Om det redan finns en hög med kort av den färgen, lägg det här kortet på den högen.
4. Om det inte finns någon hög med kort av den färgen, gör du en ny hög med just den kortfärgen.
5. Om du fortfarande har ett kort på handen, gå tillbaka till det andra steget.
6. Om det inte finns något kort kvar på din hand sorteras korten. Du är klar.

Sortering efter nummer

Detta är exempel på algoritmer för att sortera en hög med kort med många olika nummer så att numren hamnar i ordning.

Spelarna börjar med en bunt kort som inte har sorterats.

Första algoritmen

Denna algoritm går igenom kortstapeln, ett kort i taget. Kortet jämförs med nästa kort i stapeln. Observera att denna position endast ändras i steg 6. Denna algoritm kallas bubbelsortering. Den är långsam.

1. Om kortstapeln är tom, eller om den bara innehåller ett kort, är den sorterad och du är klar.
2. Ta kortstapeln. Titta på det första kortet (det översta) i högen.
3. Kortet du tittar på är kort A. Kort A befinner sig för närvarande i stapel P.
4. Om det inte finns några fler kort i högen efter kort A, gå till steg 8.
5. Nästa kort i högen är kort B.
6. Om kort B har en lägre siffra än kort A byter du om positionerna för kort A och B. Kom ihåg att du gjorde detta. När du byter kort får du inte ändra positionen P.
7. Om det finns ett annat kort i högen efter position P, titta på det och gå tillbaka till steg 3.
8. Om du inte bytte ut positionen på något kort under den senaste körningen är du klar; kortstapeln är sorterad.
9. I annat fall går du tillbaka till steg 2.

Steg-för-steg-exempel

Låt oss ta en stapel kort med siffrorna "5 1 4 2 8" och sortera dem från minsta till största nummer med hjälp av denna algoritm. I varje steg jämför algoritmen de element som är skrivna i fetstil. Den översta delen av kortstapeln ligger till vänster.

Första passet:
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 4 2 8 ) Här jämför algoritmen de två första elementen och byter ut dem.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Dessa element är redan i ordning, så algoritmen byter inte ut dem.
Andra passet:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 5 8 )
Nu är kortstapeln redan sorterad, men det vet inte vår algoritm. Algoritmen behöver ett helt pass utan byte för att veta att den är sorterad.
Tredje passet:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Slutligen är matrisen sorterad och algoritmen kan avslutas.

Historia

Detta är en lättförståelig algoritm för sortering. Datorforskare kallar den för bubbelsortering, eftersom mindre element kommer upp i toppen och ändrar sin position vid varje körning. Tyvärr är algoritmen inte särskilt bra, eftersom det krävs lång tid (många genomgångar av kortstapeln) för att sortera den.

Andra algoritmen

Den här algoritmen använder en annan idé. Ibland är det svårt att lösa ett problem, men problemet kan ändras så att det består av enklare problem som är lättare att lösa. Detta kallas rekursion. Det är svårare att förstå än det första exemplet, men det ger en bättre algoritm.

Grundläggande idé

1. Om det inte finns några kort i högen, eller om det bara finns ett kort i högen, är den sorterad och du är klar.
2. Dela kortstapeln i två ungefär lika stora halvor. Om det finns ett udda antal kort kommer en av de två staplarna att ha ett kort mer än den andra.
3. Sortera var och en av de två staplarna med hjälp av den här algoritmen (för varje stapel, börja med punkt 1 i listan).
4. Slå ihop de två sorterade staplarna enligt beskrivningen nedan.
5. Resultatet är en sorterad stapel kort. Du är klar.

Slå ihop två staplar

Detta fungerar med två kortstaplar. En av dem kallas A, den andra kallas B. Det finns en tredje stapel som är tom i början, kallad C. I slutet kommer den att innehålla resultatet.

1. Om antingen stapel A eller stapel B är tom, lägg alla kort från den stapel som inte är tom ovanpå stapel C. Du är klar, stapel C är resultatet av sammanslagningen. (Observera: ta hela stapeln och lägg den på stapel C; om du gör det kort för kort ändras ordningen och det fungerar inte som det ska).
2. Titta på de översta korten i stapel A och stapel B. Lägg det kort som har det lägsta numret ovanpå stapel C. Om det inte fanns några kort i stapel C kommer den nu att ha ett kort.
3. Om det finns kort kvar i antingen stapel A eller stapel B går du tillbaka till steg 1 för att sortera dem.

Historia

John von Neumann utvecklade denna algoritm 1945. Han kallade den inte för Sortering efter nummer, utan för Mergesort. Det är en mycket bra algoritm för sortering jämfört med andra.

Tredje algoritmen

Den första algoritmen tar mycket längre tid att sortera korten än den andra, men den kan förbättras (göras bättre). När man tittar på bubbelsortering kan man konstatera att kort med höga nummer flyttas från toppen av stapeln ganska snabbt, men att kort med låga nummer längst ner i stapeln tar lång tid på sig att stiga (flyttas till toppen). För att förbättra den första algoritmen har vi följande idé:

Istället för att jämföra två kort som ligger bredvid varandra, väljer man i början ett "specialkort". Alla andra kort jämförs sedan med detta kort.

1. Vi börjar med en stapel A. Det kommer att finnas två andra staplar, B och C, som kommer att skapas senare.
2. Om stapel A inte har några kort, eller om den bara har ett kort, är vi klara med sorteringen.
3. Ett kort plockas från stapel A, om möjligt slumpmässigt. Detta kallas för en pivot.
4. Alla återstående kort i stapel A jämförs med denna pivot. Kort med ett mindre antal hamnar i stapel B, de med ett lika stort eller större antal hamnar i stapel C.
5. Om det finns kort i stapel B eller C måste dessa staplar sorteras med samma algoritm (börja vid post 1 i listan för både stapel B och C i tur och ordning).
6. Uppfyllt. Den sorterade kortstapeln har först den sorterade stapeln B, sedan pivot och sedan den sorterade stapeln C.

Historia

Denna algoritm utvecklades av C. A. R. Hoare 1960. Det är en av de mest använda algoritmerna för sortering idag. Den kallas Quicksort.

Animation som visar hur en bubbelsortering fungerar


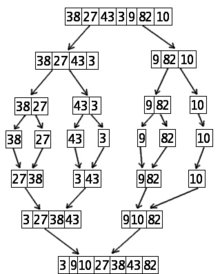
Sortering av 7 nummer med hjälp av den andra algoritmen för sortering efter nummer (Mergesort)


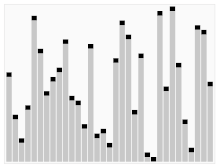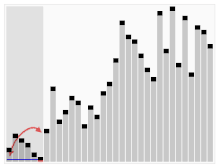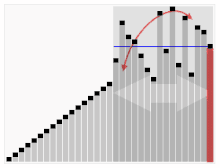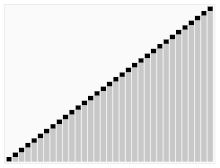
Den tredje algoritmen för sortering av kort. Elementet med den röda stapeln väljs som vändpunkt. I början är det elementet helt till höger. Denna algoritm kallas Quicksort.

Sätta ihop algoritmer

Om spelarna har kort med färger och nummer kan de sortera dem efter färg och nummer om de gör algoritmen "sortering efter färger", sedan algoritmen "sortering efter nummer" för varje färgad stapel och sedan lägger ihop staplarna.

Algoritmerna för sortering efter antal är svårare än algoritmen för sortering efter färg, eftersom de kan behöva göra om stegen många gånger. Man skulle kunna säga att sortering efter nummer är mer komplicerad.

Relaterade sidor

• Den euklidiska algoritmen upptäcktes för över 2000 år sedan. Den kan hitta den största gemensamma divisorn av två tal.