Sannolikhetsrum
Sannolikhetsrum är en matematisk modell som används för att beskriva vetenskapliga experiment Ett sannolikhetsrum består av tre delar:
- En provyta som innehåller en förteckning över alla möjliga utfall.
- En uppsättning händelser. Varje händelse associerar noll eller flera utfall.
- En funktion som tilldelar varje händelse sannolikheter.
Ett utfall är resultatet av en enda tillämpning av modellen. Eftersom enskilda resultat kan vara av liten praktisk nytta används mer komplexa händelser för att karakterisera grupper av resultat. Samlingen av alla sådana händelser är en σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}} 
. Slutligen finns det ett behov av att specificera varje händelses sannolikhet att inträffa. Detta görs med hjälp av sannolikhetsmåttfunktionen P.
När sannolikhetsområdet väl är etablerat antas att "naturen" gör sitt drag och väljer ett enda resultat, ω, från provrymden Ω. Alla händelser i F {\displaystyle \scriptstyle {\mathcal {F}}} som innehåller det valda utfallet ω (kom ihåg att varje händelse är en delmängd av Ω) sägs "ha inträffat". Det urval som naturen gör sker på ett sådant sätt att om experimentet skulle upprepas ett oändligt antal gånger, skulle de relativa frekvenserna för varje händelse sammanfalla med de sannolikheter som funktionen P föreskriver.
Den framstående sovjetiska matematikern Andrej Kolmogorov introducerade begreppet sannolikhetsrum tillsammans med andra sannolikhetsaxiom på 1930-talet.
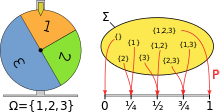
Modellering av ett lyckohjul med hjälp av sannolikhetsutrymme
Frågor och svar
Fråga: Vad är ett sannolikhetsområde?
S: Ett sannolikhetsområde är en matematisk modell som används för att beskriva vetenskapliga experiment. Den består av tre delar: ett provrum som listar alla möjliga utfall, en uppsättning händelser som associerar noll eller fler utfall och en funktion som tilldelar varje händelse sannolikheter.
F: Vad består provrymden av?
S: Urvalsutrymmet består av alla möjliga utfall, ofta skrivet som Ω {\displaystyle \Omega } och ett utfall som ω {\displaystyle \omega }. .
F: Vad är ett resultat?
S: Ett utfall är resultatet av en enda körning av modellen.
F: Vad används händelser för i sannolikhetsrum?
S: Händelser används för att karakterisera grupper av utfall eftersom enskilda utfall kan vara av liten praktisk nytta. Samlingen av alla sådana händelser kallas σ-algebra, ibland skriven som F {\displaystyle {\mathcal {F}}} .
F: Hur tilldelas sannolikheter till varje händelse?
S: Sannolikheter tilldelas varje händelse med hjälp av sannolikhetsmåttfunktionen P.
Fråga: Vem introducerade begreppet sannolikhetsrum? Svar: Den framstående sovjetiska matematikern Andrey Kolmogorov introducerade begreppet sannolikhetsrum tillsammans med andra sannolikhetsaxiom på 1930-talet.
