Sannolikhet
Sannolikhet är en del av tillämpad matematik. Den har att göra med slumpen, studiet av saker som kan hända eller inte kan hända.
Med hjälp av sannolikhet kan du till exempel visa att om du kastar ett mynt upp i luften och låter det landa, kommer det i hälften av fallen att landa med ena sidan uppåt och i hälften av fallen med den andra sidan uppåt. Många mynt har en bild av en känd persons ansikte på ena sidan och något annat på den andra sidan. Ofta kallar folk sidan med ansiktet för "krona" och den andra sidan för "klave".
Sannolikheten (p) för en händelse ligger alltid mellan noll (omöjligt) och ett (säkert).
Om vi kastar en tärning (plural: tärning) är chansen att den hamnar på 1 1/6 (eftersom det finns 6 nummer på en tärning). Chansen att den hamnar på 2 är också 1/6. Detta beror på att den kan landa på 1, 2, 3, 4, 5 eller 6. Chansen att ett tal mellan 1 och 6 landar är 1. Varje gång vi kastar tärningen kommer den alltid att landa på ett tal mellan 1 och 6.
Sannolikhet kan beräknas med hjälp av matematik. Om du t.ex. kastar sex tärningar är chansen att du får ett tal som är större än tio inte självklar, men den kan räknas ut med hjälp av matematik och vetenskap.
En av de mest intressanta sakerna med slumpen är att man för att räkna ut sannolikheten för att två saker kommer att inträffa båda två multiplicerar de två sannolikheterna med varandra. Anta till exempel att du vill veta sannolikheten för att kasta två tärningar och få en viss kombination (det kan vara två 6:or eller en 3:a och sedan en 5:a, vilka två som helst). Möjligheten att få en 3:a är en på sex (⅙) och möjligheten att få en 5:a är också en på sex, så chansen att få en 3:a och sedan en 5:a är ⅙×⅙=⅟36. Om det talet uttrycks som någonstans mellan 0 och 1 är det lika med 0,027...7, vilket är ganska lågt. Möjligheten att få en 3, sedan en 5 och sedan en 2 skulle vara ⅙×⅙×⅙=⅟216 eller 0,00463, vilket är en mycket lägre sannolikhet.
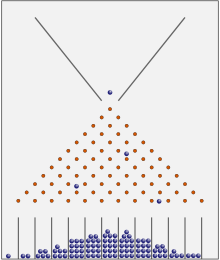
I en bönmaskin eller Galtonbox hamnar de flesta bollar nära mitten. På lång sikt kommer de att visa en normalfördelning.
Sannolikhetsidéer
Personer som Jacob Bernoulli, Pierre-Simon Laplace och Christiaan Huygens använde ordet sannolikhet, enligt beskrivningen ovan. Andra människor tänkte på frekvenser; detta begrepp om sannolikhet brukar kallas frekvenssannolikhet.
Relaterade sidor
- Förteckning över matematiska ämnen
- Sannolikhetslära
Frågor och svar
F: Vad är sannolikhet?
S: Sannolikhet är en del av den tillämpade matematiken som handlar om studiet av saker som kan hända eller inte kan hända.
F: Hur kan sannolikhet uttryckas?
S: Sannolikhet kan uttryckas som ett tal mellan noll (omöjligt) och ett (säkert).
F: Vad är ett exempel på hur man använder sannolikhet?
S: Ett exempel på att använda sannolikhet är att visa att om man kastar ett mynt upp i luften och låter det landa, kommer det i hälften av fallen att landa med ena sidan uppåt och i hälften av fallen med den andra sidan uppåt.
F: Hur beräknar man sannolikheten för att kasta två tärningar och få en viss kombination?
S: För att beräkna sannolikheten för att kasta två tärningar och få en viss kombination multiplicerar du deras två sannolikheter med varandra. Om du till exempel vill veta hur stor möjligheten är att få en 3 och sedan en 5, skulle det vara 1/6 x 1/6 = 1/36.
F: Vad betyder "svans" när man talar om mynt?
S: När man pratar om mynt avser "klave" den sida utan ansikte eller bild på den.
F: Hur sannolikt är det att kasta sex tärningar och få ett tal som är större än tio? S: Sannolikheten för att kasta sex tärningar och få ett tal som är större än tio kan räknas ut med hjälp av matematik och vetenskap men är inte självklar.
F: Vad händer när man multiplicerar två sannolikheter med varandra?
S: När du multiplicerar två sannolikheter med varandra beräknar du chansen att båda sakerna kommer att inträffa samtidigt.
Sök