Bandgap | energiområde i ett fast ämne där inga elektrontillstånd kan existera

Inom halvledarfysik

Forskare använder bandgapet för att förutsäga om ett fast ämne kommer att leda elektricitet. De flesta elektroner (så kallade valenselektroner) dras till kärnan i bara en atom. Men om en elektron har tillräckligt med energi för att flyga bort från den närmaste kärnan kan den delta i flödet av elektrisk ström mellan de många atomer som utgör fast substans. De elektroner som inte är fast knutna till bara en atomkärna kallas för ledningsbandet.

I halvledare och isolatorer visar kvantmekaniken att elektroner endast finns i ett antal energiband. Elektroner är förbjudna från andra energinivåer. Termen bandgap avser energidifferensen mellan toppen av valensbandet och botten av ledningsbandet. Elektroner kan hoppa från ett band till ett annat. En elektron behöver dock en viss mängd energi för att hoppa från ett valensband till ett ledningsband. Energimängden som behövs skiljer sig åt mellan olika material. Elektroner kan få tillräckligt med energi för att hoppa till ledningsbandet genom att absorbera antingen en fonon (värme) eller en foton (ljus).

En halvledare är ett material med ett litet men icke-noll bandgap som beter sig som en isolator vid absolut nollpunkt (0 K), men som tillåter värme att excitera elektroner tillräckligt mycket för att hoppa in i ledningsbandet vid temperaturer som ligger under smältpunkten. Ett material med ett stort bandgap är däremot en isolator. I ledare kan valens- och ledningsbanden överlappa varandra, vilket innebär att de kanske inte har något bandgap.

Ledningsförmågan hos inneboende halvledare är starkt beroende av bandgapet. De enda tillgängliga bärarna för ledning är de elektroner som har tillräckligt med värmeenergi för att exciteras över bandgapet.

Bandgapsteknik är processen för att kontrollera eller ändra bandgapet hos ett material genom att kontrollera sammansättningen av vissa halvledarlegeringar, t.ex. GaAlAs, InGaAs och InAlAs. Det är också möjligt att konstruera skiktade material med alternerande sammansättningar med hjälp av tekniker som molekylärstråleepitaxi. Dessa metoder används vid konstruktion av HBT:er (heterojunction bipolar transistorer), laserdioder och solceller.

Det är svårt att dra en gräns mellan halvledare och isolatorer. Ett sätt är att betrakta halvledare som en typ av isolator med ett smalt bandgap. Isolatorer med en större bandgap, vanligtvis större än 3 eV, placeras inte i halvledargruppen och uppvisar i allmänhet inte halvledarbeteende under praktiska förhållanden. Elektronrörligheten spelar också en roll när det gäller att bestämma ett materials informella gruppering som halvledare.

Halvledarnas bandgapsenergi tenderar att minska med stigande temperatur. När temperaturen ökar ökar amplituden för atomvibrationer, vilket leder till större interatomära avstånd. Interaktionen mellan gitterfononerna och de fria elektronerna och hålen påverkar också bandgapet en aning. Sambandet mellan bandgapsenergi och temperatur kan beskrivas med Varshnis empiriska uttryck,

E g ( T ) = E g ( 0 ) - α T 2 T + β {\displaystyle E_{g}(T)=E_{g}(0)-{\frac {\alpha T^{2}}}{T+\beta }}} , där E_g (0), α och β är materialkonstanter.

I en vanlig halvledarkristall är bandgapet fast på grund av kontinuerliga energitillstånd. I en kvantprickkristall är bandgapet storleksberoende och kan ändras för att producera ett antal energier mellan valensbandet och konduktionsbandet. Detta kallas också för kvantinlåsningseffekt.

Bandgapet beror också på trycket. Bandgapet kan vara antingen direkt eller indirekt, beroende på den elektroniska bandstrukturen.

Matematisk tolkning

Klassiskt sett ges förhållandet mellan sannolikheterna för att två tillstånd med en energidifferens ΔE ska upptas av en elektron av Boltzmannfaktorn:

e ( - Δ E k T ) {\displaystyle e^{\left({\frac {-\Delta E}{kT}}\right)}}

där:

• e är Eulers tal (basen för naturliga logaritmer).
• ΔE är energidifferensen
• k är Boltzmannkonstanten
• T är temperaturen.

Vid Fermi-nivån (eller den kemiska potentialen) är sannolikheten för att ett tillstånd är upptaget ½. Om Fermi-nivån ligger mitt i ett bandgap på 1 eV är sannolikheten e⁻²⁰ eller cirka 2,0⋅10⁻⁹ vid rumstemperaturens värmeenergi på 25,9 meV.

Solceller

Elektroner kan exciteras av både ljus och värme. Bandgapet bestämmer vilken del av solspektrumet en solcell absorberar. En luminescerande solcellskonverterare använder ett luminescerande medium för att nedkonvertera fotoner med energier över bandgapet till fotonenergier som ligger närmare bandgapet hos den halvledare som utgör solcellen.

Förteckning över bandgap

Material	Symbol	Bandgap (eV) vid 302 K	Referens
Kisel	Si	1.11
Selen	Se	1.74
Germanium	Ge	0.67
Kiselkarbid	SiC	2.86
Aluminiumfosfid	AlP	2.45
Aluminiumarsenid	AlAs	2.16
Aluminiumantimonid	AlSb	1.6
Aluminiumnitrid	AlN	6.3
Diamant	C	5.5
Gallium(III)fosfid	GaP	2.26
Gallium(III)arsenid	GaAs	1.43
Galliumnitrid (III)	GaN	3.4
Gallium(II)sulfid	GaS	2.5
Galliumantimonid	GaSb	0.7
Indiumantimonid	InSb	0.17
Indiumnitrid (III)	InN	0.7
Indium(III)fosfid	InP	1.35
Indium(III)arsenid	InAs	0.36
Järndisilicid	β-FeSi2	0.87
Zinkoxid	ZnO	3.37
Zinksulfid	ZnS	3.6
Zinkselenid	ZnSe	2.7
Zink tellurid	ZnTe	2.25
Kadmiumsulfid	CdS	2.42
Kadmiumselenid	CdSe	1.73
Kadmiumtellurid	CdTe	1.49
Bly(II)sulfid	PbS	0.37
Bly(II)selenid	PbSe	0.27
Bly(II)tellurid	PbTe	0.29
Koppar(II)oxid	CuO	1.2
Koppar(I)oxid	Cu2 O	2.1

 
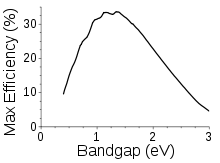
Shockley-Queisser-gränsen anger den högsta möjliga verkningsgraden för en solcell med en enda förbindelse i okoncentrerat solljus, som en funktion av halvledarens bandgap. Om bandgapet är för högt kan de flesta fotoner i dagsljuset inte absorberas. Om det är för lågt har de flesta fotoner mycket mer energi än vad som krävs för att excitera elektroner över bandgapet, och resten går till spillo. De halvledare som vanligen används i kommersiella solceller har bandgap nära toppen av denna kurva, till exempel kisel (1,1eV) eller CdTe (1,5eV). Shockley-Queisser-gränsen kan överskridas genom tandemsolceller, genom att koncentrera solljuset på cellen och andra metoder.  


Bandstruktur för halvledare.  

Inom fotonik och fonik

I fotonik är bandgap eller stoppband områden av fotonfrekvenser där inga fotoner kan överföras genom ett material om man bortser från tunneleffekter. Ett material som uppvisar detta beteende kallas en "fotonisk kristall".

Liknande fysik gäller för fononer i en fononisk kristall.