Kvantmekanik – Vad är kvantfysik? En enkel förklaring och översikt
Lär dig kvantmekanik enkelt: förstå våg‑partikeldualitet, subatomära partiklar och hur kvantfysik förklarar ljus och materia — klar, begriplig översikt för nybörjare.
Kvantmekaniken förklarar hur universum fungerar på mycket små skalor — mindre än atomer. Den kallas också kvantfysik eller kvantteori. Ordet Mekanik syftar på den del av fysiken som beskriver hur saker rör sig, och kvantum kommer från det latinska ordet för "hur mycket". Ett energikvant är den minsta möjliga mängden energi som kan bytas eller avges i ett system, och kvantmekaniken beskriver hur sådana kvanta uppträder och interagerar.
Atomer betraktades länge som de minsta byggstenarna i materia, men modern forskning visar att atomer består av ännu mindre subatomära partiklar — till exempel protoner, neutroner och elektroner. Kvantmekaniken förklarar hur dessa partiklar beter sig, både som individuella objekt och i samspel med varandra.
Våg–partikel-dualitet och vågor
Kvantteorin visar att partiklar kan uppvisa egenskaper som liknar vågor, och att vågor kan uppvisa partikelegenskaper. Denna våg-partikel-dualiteten innebär att till exempel elektromagnetiska vågor — inklusive ljus — ibland beter sig som vågor (spridning, interferens) och ibland som partiklar (diskreta energipaket, fotoner). De är alltså inte två helt separata typer av saker utan två sidor av samma fenomen.
Grundläggande principer
- Kvantisering: Vissa storheter (t.ex. energi i en atom) kan bara anta bestämda, diskreta värden. Det är därför elektroner i atomer befinner sig i bestämda energinivåer.
- Superposition: Ett kvantsystem kan samtidigt befinna sig i flera tillstånd tills en mätning görs. Det innebär att ett elektron kan beskrivas av en vågfunktion som innehåller flera möjliga utfall samtidigt.
- Osäkerhetsprincipen: Formulerad av Heisenberg — vissa par av egenskaper, som position och rörelsemängd, kan inte mätas med godtycklig precision samtidigt. Ju mer exakt du känner en egenskap, desto mindre exakt kan du känna den andra.
- Intrassling (entanglement): Två eller flera partiklar kan bli sammanlänkade så att mätningen av en omedelbart påverkar den andra, oavsett avstånd. Detta leder till märkliga korrelationer som testats i så kallade Bell-test.
Mätproblem och vågfunktion
Kvantmekaniken beskriver system med en vågfunktion som talar om sannolikheter för olika utfall. När vi gör en mätning "kollapsar" vågfunktionen till ett bestämt utfall — en process som i praktiken är väl beskriven av teorin men som också lett till filosofiska och tolkande frågor (t.ex. Schrödingers katt-tankeexperiment). Den centrala ekvationen som beskriver hur vågfunktionen utvecklas i tid är Schrödingerekvationen.
Matematik och komplexitet
Den matematik som används i kvantmekanik är i grunden linjär algebra (vektorer och matriser), differentialekvationer och operator-teori, men kan bli mycket avancerad i praktiska tillämpningar. Trots den matematiska svårigheten ger kvantmekaniken mycket precisa förutsägelser som stämmer oerhört väl med experiment.
Tillämpningar i vardag och teknik
Kvantmekanik är inte bara abstrakt teori — den ligger bakom många tekniker vi använder dagligen:
- Transistorer och halvledare (grund för alla moderna datorer och telefoner).
- Lasrar och LED-lampor.
- Magnetisk resonanstomografi (MRI) inom medicin.
- Atomur som ger extremt noggrann tidmätning.
- Utveckling av kvantdatorer och kvantkryptografi, som utnyttjar superposition och intrassling för nya typer av beräkningar och säkra kommunikationsmetoder.
Mycket av modern fysiken och kemin förklaras och styrs av kvantmekanikens regler — från hur molekyler binds ihop till varför vissa material leder elektricitet medan andra isolerar.
Historik i korthet
Kvantfysiken växte fram i början av 1900‑talet. Max Planck introducerade idén om kvanta för att förklara svartkroppsstrålning, Einstein förklarade fotoelektriska effekten med ljusets kvanta (fotoner), och forskare som Niels Bohr, Werner Heisenberg och Erwin Schrödinger byggde de teoretiska grunderna som sedan utvecklades vidare.
Experimentell bekräftelse
Kvantmekanikens förutsägelser har upprepade gånger bekräftats av experiment: dubbelspaltsexperimentet visar våg‑partikel‑beteende, Stern–Gerlach‑experimentet demonstrerar kvantiserade spinnriktningar, och moderna Bell‑tester visar att intrassling ger icke‑lokala korrelationer som inte kan förklaras av klassiska dolda variabler.
Sammanfattningsvis beskriver kvantmekaniken den fysiska världen på de minsta skalorna. Den är både teoretiskt djup och praktiskt viktig — svår att intuitivt förstå eftersom våra vardagsupplevelser bygger på klassiska, makroskopiska lagar, men ändå oerhört framgångsrik i att förutsäga och förklara naturens beteende på mikronivå.
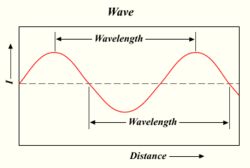
Våglängden för en ljusvåg
Vågor och fotoner
Fotoner är partiklar av punktstorlek, mindre än atomer. Fotoner är som "paket" eller energipaket. Ljuskällor som t.ex. stearinljus eller lasrar producerar ljus i bitar som kallas fotoner.
Ju fler fotoner en lampa producerar, desto ljusare blir ljuset. Ljus är en form av energi som beter sig som vågor i vatten eller radiovågor. Avståndet mellan toppen av en våg och toppen av nästa våg kallas för en "våglängd". Varje foton bär på en viss mängd, eller "kvantum", energi beroende på dess våglängd.
Ljusets färg beror på dess våglängd. Färgen violett (den nedersta eller innersta färgen i regnbågen) har en våglängd på cirka 400 nm ("nanometer"), vilket motsvarar 0,00004 centimeter eller 0,000016 tum. Fotoner med våglängder på 10-400 nm kallas ultraviolett (eller UV) ljus. Sådant ljus kan inte ses av det mänskliga ögat. I andra änden av spektrumet är rött ljus ungefär 700 nm. Infrarött ljus är ungefär 700 nm till 300 000 nm. Människans ögon är inte heller känsliga för infrarött ljus.
Våglängder är inte alltid så små. Radiovågor har längre våglängder. Våglängden för en FM-radio kan vara flera meter lång (till exempel sänder stationer som sänder på 99,5 FM ut radioenergi med en våglängd på cirka 3 meter, vilket motsvarar cirka 10 fot). Varje foton har en viss mängd energi som är relaterad till dess våglängd. Ju kortare våglängd en foton har, desto större är dess energi. Till exempel har en ultraviolett foton mer energi än en infraröd foton.
Våglängden och frekvensen (antalet gånger som vågen går upp i topp per sekund) är omvänt proportionella, vilket innebär att en längre våglängd har en lägre frekvens och vice versa. Om ljusets färg är infrarött (lägre frekvens än rött ljus) kan varje foton värma upp det den träffar. Så om en stark infraröd lampa (en värmelampa) riktas mot en person kommer personen att känna sig varm, eller till och med varm, på grund av den energi som lagras i de många fotonerna. Den infraröda lampans yta kan till och med bli tillräckligt varm för att bränna någon som rör vid den. Människor kan inte se infrarött ljus, men vi kan känna strålningen i form av värme. En person som till exempel går förbi en tegelbyggnad som har värmts upp av solen kommer att känna värme från byggnaden utan att behöva röra vid den.
De matematiska ekvationerna i kvantmekaniken är abstrakta, vilket innebär att det är omöjligt att med säkerhet veta exakt vilka fysiska egenskaper en partikel har (t.ex. dess position eller rörelseförmåga). I stället ger en matematisk funktion som kallas vågfunktion information om sannolikheten för att en partikel har en viss egenskap. Vågfunktionen kan till exempel tala om vilken sannolikhet det är att en partikel finns på en viss plats, men den kan inte med säkerhet säga var den finns. På grund av denna osäkerhet och andra faktorer kan du inte använda klassisk mekanik (den fysik som beskriver hur stora föremål rör sig) för att förutsäga kvantpartiklars rörelse.
Ultraviolett ljus har en högre frekvens än violett ljus, vilket innebär att det inte ens hör till det synliga ljusområdet. Varje foton i det ultravioletta området har mycket energi, tillräckligt för att skada hudceller och orsaka solbränna. Faktum är att de flesta former av solbränna inte orsakas av värme, utan av att den höga energin i solens UV-strålar skadar hudcellerna. Även högre frekvenser av ljus (eller elektromagnetisk strålning) kan tränga djupare in i kroppen och orsaka ännu mer skada. Röntgenstrålar har så mycket energi att de kan gå djupt in i människokroppen och döda celler. Människor kan inte se eller känna ultraviolett ljus eller röntgenstrålar. De kan bara veta att de har varit under ett sådant högfrekvent ljus när de får en strålningsbränna. På områden där det är viktigt att döda bakterier används ofta ultravioletta lampor för att förstöra bakterier, svampar osv. Röntgenstrålar används ibland för att döda cancerceller.
Kvantmekaniken började när man upptäckte att om en partikel har en viss frekvens måste den också ha en viss mängd energi. Energin är proportionell mot frekvensen (E ∝ f). Ju högre frekvens, desto mer energi har en foton och desto mer skada kan den göra. Kvantmekaniken växte senare till för att förklara atomernas inre struktur. Kvantmekaniken förklarar också hur en foton kan interferera med sig själv och många andra saker som den klassiska fysiken aldrig hade kunnat föreställa sig.

Svart till vänster är ultraviolett (hög frekvens), svart till höger är infrarött (låg frekvens).
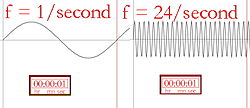
Bildmässig beskrivning av frekvensen
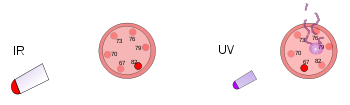
Till vänster står en plasttermometer under en ljus värmelampa. Den infraröda strålningen värmer termometern men skadar den inte. Till höger träffas en annan plasttermometer av ett ultraviolett ljus med låg intensitet. Denna strålning skadar men värmer inte termometern.
Kvantisering
Max Planck upptäckte sambandet mellan frekvens och energi. Ingen tidigare hade någonsin gissat att frekvensen är direkt proportionell mot energin (det betyder att när den ena av dem fördubblas, så fördubblas också den andra). I vad som kallas naturliga enheter skulle det tal som representerar frekvensen hos en foton också representera dess energi. Ekvationen skulle då vara:
Det betyder att energi är lika med frekvens.
Men på det sätt som fysiken utvecklades fanns det inget naturligt samband mellan de enheter som användes för att mäta energi och de enheter som vanligtvis används för att mäta tid (och därmed frekvens). Så den formel som Planck utarbetade för att få siffrorna att stämma var följande:
eller energi är lika med h gånger frekvensen. Detta h är ett tal som kallas Plancks konstant efter dess upptäckare.
Kvantmekaniken bygger på kunskapen att en foton med en viss frekvens innebär en foton med en viss mängd energi. Förutom detta förhållande kan en viss typ av atom bara avge vissa frekvenser av strålning, så den kan också bara avge fotoner som har en viss mängd energi.
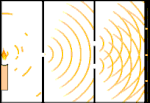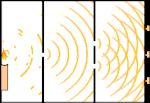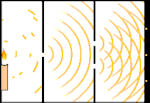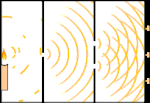
Dubbelspaltsexperiment: Ljuset går från ljuskällan till vänster till fransarna (markerade i den svarta kanten) till höger.
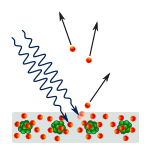
Fotoelektrisk effekt: Fotoner träffar metall och elektroner skjuts bort.
Historia
Isaac Newton trodde att ljuset bestod av mycket små saker som vi nu skulle kalla partiklar (han kallade dem "korpuskel"). Christiaan Huygens trodde att ljuset bestod av vågor. Vetenskapsmännen ansåg att en sak inte kan vara en partikel och en våg samtidigt.
Forskarna gjorde experiment för att ta reda på om ljuset bestod av partiklar eller vågor. De kom fram till att båda idéerna var riktiga - ljuset bestod på något sätt av både vågor och partiklar. Dubbelspaltsexperimentet som utfördes av Thomas Young visade att ljuset måste fungera som en våg. Den fotoelektriska effekten som upptäcktes av Albert Einstein bevisade att ljuset måste agera som partiklar som bar på specifika mängder energi, och att energierna var kopplade till deras frekvenser. Detta experimentella resultat kallas "våg-partikel-dualitet" inom kvantmekaniken. Senare upptäckte fysikerna att allting beter sig både som en våg och som en partikel, inte bara ljuset. Denna effekt är dock mycket mindre i stora objekt.
Här är några av de personer som upptäckte de grundläggande delarna av kvantmekaniken: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann och Richard Feynman. De utförde sitt arbete under första hälften av 1900-talet.

Från vänster till höger: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Bortom Planck
Kvantmekanikens formler och idéer användes för att förklara det ljus som kommer från glödande väte. Kvantteorin om atomen måste också förklara varför elektronen stannar i sin bana, vilket andra idéer inte kunde förklara. Det följde av de äldre idéerna att elektronen måste falla in i atomens centrum eftersom den till en början hålls i sin omloppsbana av sin egen energi, men den skulle snabbt förlora sin energi när den roterar i sin omloppsbana. (Detta beror på att elektroner och andra laddade partiklar var kända för att avge ljus och förlora energi när de ändrade hastighet eller vände sig om).
Vätgaslampor fungerar som neonlampor, men neonlampor har sin egen unika grupp av färger (och frekvenser) av ljus. Forskare lärde sig att de kunde identifiera alla grundämnen genom de ljusfärger de producerar. De kunde bara inte lista ut hur frekvenserna bestämdes.
Sedan kom en schweizisk matematiker vid namn Johann Balmer på en ekvation som angav vad λ (lambda, för våglängd) skulle vara:
där B är ett tal som Balmer fastställde till 364,56 nm.
Denna ekvation fungerade endast för det synliga ljuset från en väteblixt. Men senare gjordes ekvationen mer generell:
där R är Rydbergkonstanten, som är lika med 0,0110 nm−1 , och n måste vara större än m.
Genom att sätta in olika tal för m och n är det lätt att förutsäga frekvenser för många typer av ljus (ultraviolett, synligt och infarkt). För att se hur detta fungerar, gå till Hyperphysics och gå ner förbi mitten av sidan. (Använd H = 1 för väte.)
År 1908 skapade Walter Ritz Ritz-kombinationsprincipen som visar hur vissa mellanrum mellan frekvenser upprepas. Detta visade sig vara viktigt för Werner Heisenberg flera år senare.
1905 använde Albert Einstein Plancks idé för att visa att en ljusstråle består av en ström av partiklar som kallas fotoner. Energin hos varje foton beror på dess frekvens. Einsteins idé är början på kvantmekanikens idé att alla subatomära partiklar som elektroner, protoner, neutroner och andra är både vågor och partiklar på samma gång. (Se bild av atom med elektronen som vågor vid atom.) Detta ledde till en teori om subatomära partiklar och elektromagnetiska vågor som kallas våg-partikel-dualitet. Detta innebär att partiklar och vågor varken var det ena eller det andra, utan hade vissa egenskaper hos båda.
År 1913 kom Niels Bohr på idén att elektroner endast kan inta vissa banor runt atomkärnan. Enligt Bohrs teori kan siffrorna m och n i ekvationen ovan representera banor. Bohrs teori sade att elektroner kan börja i en viss omloppsbana m och sluta i en viss omloppsbana n, eller att en elektron kan börja i en viss omloppsbana n och sluta i en viss omloppsbana m. Om en foton träffar en elektron kommer dess energi att absorberas, och elektronen kommer att flytta sig till en högre omloppsbana på grund av den extra energin. Enligt Bohrs teori, om en elektron faller från en högre bana till en lägre bana, måste den avge energi i form av en foton. Fotonens energi kommer att motsvara energidifferensen mellan de två banorna, och fotons energi gör att den har en viss frekvens och färg. Bohrs teori gav en bra förklaring till många aspekter av subatomära fenomen, men kunde inte svara på varför var och en av de ljusfärger som produceras av glödande väte (och av glödande neon eller något annat grundämne) har en egen ljusstyrka, och ljusstyrkan är alltid densamma för varje grundämne.
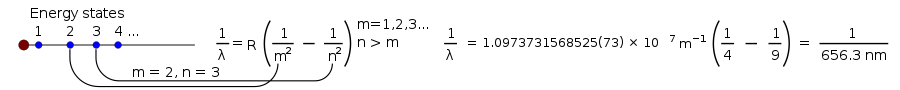
När Niels Bohr kom med sin teori visste man det mesta om ljuset från en väteblixt, men forskarna kunde fortfarande inte förklara hur ljusstarka de linjer som produceras av glödande väte är.
Werner Heisenberg tog på sig uppgiften att förklara ljusstyrkan eller "intensiteten" i varje linje. Han kunde inte använda någon enkel regel som den som Balmer hade kommit på. Han var tvungen att använda den klassiska fysikens mycket svåra matematik som räknar ut allt i termer av saker som en elektrons massa (vikt), en elektrons laddning (statisk elektrisk styrka) och andra små mängder. Den klassiska fysiken hade redan svar på hur ljusstyrka de färgband som en väteblixt ger upphov till är, men den klassiska teorin sade att det borde vara en kontinuerlig regnbåge och inte fyra separata färgband. Heisenbergs förklaring är följande:
Det finns någon lag som säger vilka ljusfrekvenser glödande väte producerar. Den måste förutsäga att frekvenserna är utspridda när de berörda elektronerna rör sig mellan banor nära atomkärnan (centrum), men den måste också förutsäga att frekvenserna kommer att komma närmare och närmare varandra när vi tittar på vad elektronen gör när den rör sig mellan banor längre och längre ut. Den ska också förutsäga att intensitetsskillnaderna mellan frekvenserna kommer närmare och närmare varandra när vi går utåt. När den klassiska fysiken redan ger de rätta svaren med hjälp av en uppsättning ekvationer måste den nya fysiken ge samma svar men med hjälp av olika ekvationer.
Den klassiska fysiken använder Joseph Fouriers matematiska metoder för att skapa en matematisk bild av den fysiska världen. Den använder samlingar av jämna kurvor som tillsammans bildar en jämn kurva som i det här fallet ger intensiteter för ljus av alla frekvenser från ett visst ljus. Men det stämmer inte eftersom den jämna kurvan endast visas vid högre frekvenser. Vid lägre frekvenser finns det alltid isolerade punkter och ingenting förbinder punkterna. Så för att göra en karta över den verkliga världen var Heisenberg tvungen att göra en stor förändring. Han var tvungen att göra något för att välja ut endast de siffror som skulle stämma överens med det som sågs i naturen. Ibland säger folk att han "gissade" dessa ekvationer, men han gjorde inga blinda gissningar. Han hittade det han behövde. De siffror som han räknade ut skulle sätta prickar på ett diagram, men det skulle inte dras någon linje mellan prickarna. Att göra en "graf" med enbart punkter för varje beräkning skulle ha slösat bort massor av papper och inte ha lett till något resultat. Heisenberg hittade ett sätt att effektivt förutsäga intensiteterna för olika frekvenser och att organisera informationen på ett användbart sätt.
Genom att bara använda den empiriska regeln ovan, den som Balmer började använda och Rydberg förbättrade, kan vi se hur vi kan få fram en uppsättning siffror som skulle hjälpa Heisenberg att få den bild han ville ha:
Regeln säger att när elektronen rör sig från en omloppsbana till en annan får den antingen mer eller mindre energi, beroende på om den kommer längre bort från centrum eller närmare det. Vi kan alltså placera dessa banor eller energinivåer som rubriker längs toppen och sidan av ett rutnät. Av historiska skäl kallas den lägsta banan för n, och nästa bana utåt kallas n - a, därefter kommer n - b och så vidare. Det är förvirrande att de använde negativa tal när elektronerna faktiskt fick energi, men det är så det är.
Eftersom Rydbergregeln ger oss frekvenser kan vi använda den regeln för att sätta in siffror beroende på vart elektronen tar vägen. Om elektronen börjar vid n och slutar vid n har den egentligen inte gått någonstans, så den har varken fått energi eller förlorat energi. Frekvensen är alltså 0. Om elektronen börjar vid n-a och slutar vid n har den fallit från en högre bana till en lägre bana. Om den gör det förlorar den energi, och den energi den förlorar visar sig som en foton. Fotonen har en viss mängd energi, e, och den är relaterad till en viss frekvens f genom ekvationen e = h f. Vi vet alltså att en viss förändring av omloppsbanan kommer att producera en viss frekvens av ljuset, f. Om elektronen börjar vid n och slutar vid n - a, betyder det att den har gått från en lägre omloppsbana till en högre omloppsbana. Detta sker endast när en foton med en viss frekvens och energi kommer in utifrån, absorberas av elektronen och ger den sin energi, och det är detta som gör att elektronen går ut till en högre bana. Så för att allt ska vara begripligt skriver vi den frekvensen som ett negativt tal. Det fanns en foton med en viss frekvens och nu har den tagits bort.
Vi kan alltså göra ett rutnät som detta, där f(a←b) betyder frekvensen när en elektron går från energitillstånd (bana) b till energitillstånd a (återigen, sekvenserna ser baklänges ut, men det är så de ursprungligen skrevs):
Rutnät av f
| Elektrontillstånd | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| övergång.... | ..... | ..... | ..... | ..... |
Heisenberg gjorde inte rutorna på detta sätt. Han gjorde bara den matematik som gjorde att han fick fram de intensiteter han sökte. Men för att göra det var han tvungen att multiplicera två amplituder (hur hög en våg är) för att räkna ut intensiteten. (I klassisk fysik är intensiteten lika med amplituden i kvadrat.) Han gjorde en märklig ekvation för att hantera detta problem, skrev resten av sin uppsats, gav den till sin chef och gick på semester. Dr Born tittade på sin lustiga ekvation och den verkade lite knasig. Han måste ha undrat: "Varför gav Heisenberg mig den här konstiga saken? Varför måste han göra det på det här sättet?". Sedan insåg han att han tittade på en ritning för något som han redan visste mycket väl. Han var van vid att kalla det rutnät eller den tabell som vi kunde skriva genom att till exempel göra all matematik för frekvenser för en matris. Och Heisenbergs märkliga ekvation var en regel för att multiplicera två av dem tillsammans. Max Born var en mycket, mycket bra matematiker. Han visste att eftersom de två matriser (rutnät) som multipliceras representerade olika saker (som position (x,y,z) och impuls (mv), till exempel), så får man ett svar när man multiplicerar den första matrisen med den andra och ett annat när man multiplicerar den andra matrisen med den första matrisen. Även om han inte kände till matrismatematik såg Heisenberg redan detta problem med "olika svar" och det hade stört honom. Men dr Born var en så bra matematiker att han såg att skillnaden mellan den första och den andra matrismultiplikationen alltid skulle involvera Plancks konstant, h, multiplicerad med kvadratroten av den negativa ettan, i. Så inom några dagar efter Heisenbergs upptäckt hade de redan den grundläggande matematiken för det som Heisenberg tyckte om att kalla "obestämdhetsprincipen". Med "obestämdhet" menade Heisenberg att något som en elektron inte kan fastställas förrän den blir fastställd. Den är lite som en manet som alltid krusar runt och som inte kan vara "på ett ställe" om man inte dödar den. Senare fick folk för vana att kalla det "Heisenbergs osäkerhetsprincip", vilket fick många att göra misstaget att tro att elektroner och liknande saker verkligen finns "någonstans", men att vi bara är osäkra på det i våra egna sinnen. Den tanken är felaktig. Det är inte vad Heisenberg talade om. Att ha problem med att mäta något är ett problem, men det är inte det problem som Heisenberg talade om.
Heisenbergs idé är mycket svår att förstå, men vi kan göra den tydligare med ett exempel. Först kommer vi att börja kalla dessa rutnät för "matriser", eftersom vi snart kommer att behöva tala om matrismultiplikation.
Anta att vi börjar med två typer av mätningar, position (q) och rörelse (p). År 1925 skrev Heisenberg en ekvation som liknar denna:

Han visste inte det, men denna ekvation ger en plan för hur man skriver ut två matriser (rutnät) och hur man multiplicerar dem. Reglerna för att multiplicera en matris med en annan är lite röriga, men här är de två matriserna enligt ritningen, och sedan deras produkt:
Matris för p
| Elektrontillstånd | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| övergång.... | ..... | ..... | ..... | ..... |
Matris för q
| Elektrontillstånd | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| övergång.... | ..... | ..... | ..... | ..... |
Matrisen för produkten av de två ovanstående matriserna enligt den relevanta ekvationen i Heisenbergs artikel från 1925 är:
| Elektrontillstånd | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Var:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
och så vidare.
Om matriserna vänds om skulle följande värden uppstå:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
och så vidare.
Lägg märke till att om du ändrar multiplikationsordningen ändras de tal som faktiskt multipliceras steg för steg.

Synligt ljus som avges av glödande väte. (Våglängder i nanometer.)
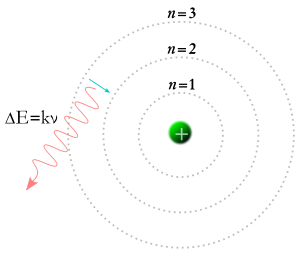
En elektron faller ner i en lägre omloppsbana och en foton skapas.
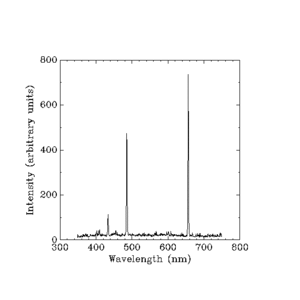
Utspridda intensiteter i godtyckliga enheter.
Bortom Heisenberg
Werner Heisenbergs arbete tycktes bryta en blockering. Mycket snart kom många olika sätt att förklara saker och ting från personer som Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli och Erwin Schrödinger. Var och en av dessa fysikers arbete är en egen historia. Den matematik som Heisenberg och tidigare personer använde sig av är inte särskilt svår att förstå, men ekvationerna blev snabbt mycket komplicerade när fysikerna tittade djupare in i atomvärlden.
Ytterligare mysterier
Under kvantmekanikens tidiga dagar föreslog Albert Einstein att om kvantmekaniken hade rätt så skulle den innebära att det fanns "spöklik verkan på avstånd". Det visade sig att kvantmekaniken hade rätt, och att det som Einstein hade använt som skäl för att förkasta kvantmekaniken faktiskt inträffade. Denna typ av "spöklik koppling" mellan vissa kvanthändelser kallas nu för "kvantförvirring".
När ett experiment sammanför två saker (fotoner, elektroner etc.) måste de ha en gemensam beskrivning inom kvantmekaniken. När de senare separeras behåller de samma kvantmekaniska beskrivning eller "tillstånd". I diagrammet är den ena egenskapen (t.ex. "uppspinn") ritad med rött och dess motsvarighet (t.ex. "nedspinn") med blått. Det lila bandet innebär att när t.ex. två elektroner sätts ihop delar paret båda egenskaperna. Båda elektronerna kan alltså visa antingen uppåtspinn eller nedåtspinn. När de senare skiljs åt, där en stannar kvar på jorden och en åker till någon planet kring stjärnan Alpha Centauri, har de fortfarande båda spinn. Med andra ord kan var och en av dem "bestämma" sig för att visa sig som en elektron med uppåtriktad spinnning eller en elektron med nedåtriktad spinnning. Men om någon senare mäter den andra elektronen måste den "bestämma" sig för att visa sig ha det motsatta spinnet.
Einstein hävdade att det var vansinnigt att tro att en elektron som tvingas visa sitt spinn på något sätt skulle få den andra elektronen att visa en motsatt egenskap på ett så stort avstånd. Han sade att de två elektronerna måste ha varit spinn-up eller spinn-down hela tiden, men att kvantmekaniken inte kunde förutsäga vilken egenskap varje elektron hade. Att inte kunna förutsäga, att bara kunna titta på en av dem med rätt experiment, innebar att kvantmekaniken inte kunde redogöra för något viktigt. Därför, sade Einstein, hade kvantmekaniken ett stort hål i den. Kvantmekaniken var ofullständig.
Senare visade det sig att experiment visade att det var Einstein som hade fel.
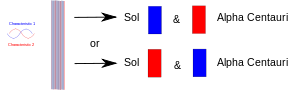
Två sammanflätade partiklar separeras: en på jorden och en som förs till en avlägsen planet. Om man mäter den ena av dem tvingas den "bestämma" vilken roll den ska ta, och den andra måste då ta den andra rollen närhelst (därefter) den mäts.
Heisenbergs osäkerhetsprincip
1925 beskrev Werner Heisenberg osäkerhetsprincipen, som säger att ju mer vi vet om var en partikel befinner sig, desto mindre kan vi veta om hur snabbt den rör sig och i vilken riktning. Med andra ord, ju mer vi vet om hastigheten och riktningen för något litet, desto mindre kan vi veta om dess position. Fysiker brukar i sådana diskussioner tala om rörelsemängd i stället för att tala om hastighet. Momentum är bara hastigheten hos något i en viss riktning gånger dess massa.
Heisenbergs osäkerhetsprincip säger att vi aldrig kan veta både var en partikel befinner sig och vilken rörelse den har. Eftersom ljus är en riklig partikel används den för att mäta andra partiklar. Det enda sättet att mäta det är att studsa ljusvågen mot partikeln och registrera resultatet. Om en ljusstråle med hög energi eller hög frekvens används kan vi säga exakt var den befinner sig, men vi kan inte säga hur snabbt den rörde sig. Detta beror på att den högenergiska fotonen överför energi till partikeln och ändrar partikelns hastighet. Om vi använder en foton med låg energi kan vi säga hur snabbt den rör sig, men inte var den är. Detta beror på att vi använder ljus med en längre våglängd. Den längre våglängden innebär att partikeln kan befinna sig var som helst längs vågens sträckning.
Principen säger också att det finns många par av mätningar för vilka vi inte kan veta båda om någon partikel (en mycket liten sak), hur mycket vi än försöker. Ju mer vi lär oss om det ena av ett sådant par, desto mindre kan vi veta om det andra.
Till och med Albert Einstein hade svårt att acceptera ett så bisarrt koncept och sa i en välkänd debatt: "Gud spelar inte tärning". Den danske fysikern Niels Bohr svarade som bekant: "Einstein, säg inte åt Gud vad han ska göra".
Användning av kvantmekaniken
Elektroner omger varje atomkärna. Kemiska bindningar förbinder atomer till molekyler. En kemisk bindning förbinder två atomer när elektroner delas mellan atomerna. Kvantmekaniken är således fysiken för kemiska bindningar och kemi. Kvantmekaniken hjälper oss att förstå hur molekyler tillverkas och vilka egenskaper de har.
Kvantmekaniken kan också hjälpa oss att förstå stora saker, t.ex. stjärnor och till och med hela universum. Kvantmekaniken är en mycket viktig del av teorin om hur universum började, den så kallade Big Bang-teorin.
Allt som består av materia dras till annan materia på grund av en grundläggande kraft som kallas gravitation. Einsteins teori som förklarar gravitationen kallas den allmänna relativitetsteorin. Ett problem inom den moderna fysiken är att vissa slutsatser från kvantmekaniken inte verkar stämma överens med den allmänna relativitetsteorin.
Kvantmekaniken är den del av fysiken som kan förklara varför all elektronisk teknik fungerar som den gör. Kvantmekaniken förklarar alltså hur datorer fungerar, eftersom datorer är elektroniska maskiner. Men konstruktörerna av den tidiga datorhårdvaran från omkring 1950 eller 1960 behövde inte tänka på kvantmekanik. Konstruktörerna av radioapparater och TV-apparater på den tiden tänkte inte heller på kvantmekanik. Men för att utforma de senaste årens kraftfullare integrerade kretsar och datorminnesteknik krävs det kvantmekanik.
Kvantmekaniken har också möjliggjort teknik som t.ex:
Varför kvantmekanik är svårt att lära sig
Kvantmekanik är ett utmanande ämne av flera skäl:
- Kvantmekaniken förklarar saker på ett helt annat sätt än vad vi lär oss om världen när vi är barn.
- För att förstå kvantmekaniken krävs mer matematik än algebra och enkel kalkyl. Det krävs också matrisalgebra, komplexa tal, sannolikhetsteori och partiella differentialekvationer.
- Fysikerna är inte säkra på vad vissa av kvantmekanikens ekvationer säger oss om den verkliga världen.
- Kvantmekaniken visar att atomer och subatomära partiklar beter sig på ett märkligt sätt, helt olikt det vi ser i vår vardag.
- Kvantmekaniken beskriver saker som är extremt små, så vi kan inte se en del av dem utan särskild utrustning, och vi kan inte se många av dem alls.
Kvantmekaniken beskriver naturen på ett sätt som skiljer sig från hur vi vanligtvis tänker på vetenskap. Den talar om för oss hur sannolikt det är att vissa saker kommer att hända, snarare än att säga att de med säkerhet kommer att hända.
Ett exempel är Youngs dubbelspaltsexperiment. Om vi skjuter enstaka fotoner (enstaka ljusenheter) från en laser mot en fotografisk film, kommer vi att se en enda ljuspunkt på den framkallade filmen. Om vi lägger en metallplåt emellan och gör två mycket smala slitsar i plåten, kommer vi att se något anmärkningsvärt när vi skjuter många fotoner mot metallplåten och de måste passera genom slitsarna. Över hela den framkallade filmen kommer vi att se en rad ljusa och mörka band. Vi kan använda matematik för att säga exakt var de ljusa banden kommer att vara och hur starkt ljuset var som skapade dem, det vill säga vi kan i förväg säga hur många fotoner som kommer att falla på varje band. Men om vi saktar ner processen och ser var varje foton landar på skärmen kan vi aldrig i förväg säga var nästa foton kommer att dyka upp. Vi kan med säkerhet veta att det är mest troligt att en foton kommer att träffa det ljusa bandet i mitten, och att det blir mindre och mindre troligt att en foton kommer att dyka upp på band längre och längre bort från mitten. Vi vet alltså med säkerhet att banden kommer att vara ljusast i centrum och bli svagare och svagare längre bort. Men vi vet aldrig med säkerhet vilken foton som kommer att hamna i vilket band.
En av de märkliga slutsatserna av kvantmekanikens teori är "Schrödingers katt"-effekten. Vissa egenskaper hos en partikel, t.ex. dess position, rörelsehastighet, rörelseriktning och "spin", kan man inte tala om förrän något mäter dem (en foton som studsar på en elektron skulle till exempel räknas som en mätning av dess position). Före mätningen befinner sig partikeln i en "superposition av tillstånd", där dess egenskaper har många värden samtidigt. Schrödinger sade att kvantmekaniken tycktes säga att om något (t.ex. en katts liv eller död) bestämdes av en kvanthändelse, så skulle dess tillstånd bestämmas av det tillstånd som blev resultatet av kvanthändelsen, men bara vid den tidpunkt då någon tittade på tillståndet för kvanthändelsen. Under tiden innan kvanthändelsens tillstånd betraktas kanske "den levande och den döda katten (ursäkta uttrycket) [är] blandade eller utspädda i lika delar".
Reducerad Plancks konstant
Folk använder ofta symbolen ℏ 

Exempel
Partikeln i en endimensionell brunn är det enklaste exemplet som visar att partikelns energi endast kan ha vissa värden. Energin sägs vara "kvantiserad". Brunnen har noll potentiell energi inom ett område och har oändlig potentiell energi överallt utanför detta område. För det endimensionella fallet i 
Med hjälp av differentialekvationer kan vi räkna ut att ψ 
eller som

Lådans väggar innebär att vågfunktionen måste ha en speciell form. Partikelns vågfunktion måste vara noll när väggarna är oändligt höga. Vid varje vägg:
Vi betraktar x = 0
- sin 0 = 0, cos 0 = 1. För att uppfylla ψ
måste cos-termen tas bort. D = 0
Tänk nu på följande:
- vid
, ψ
- Om
så är ψ
för alla x. Denna lösning är inte användbar.
- därför måste
vara sant, vilket ger oss
Vi kan se att 
Relaterade sidor
- Elektromagnetisk våg
- Elektroner
- Foton
- Kvantförveckling
- Kvantdator
- Kvanttillstånd
- Schrödingerekvation
Mer läsning
- Cox, Brian; & Forshaw, Jeff (2011). Kvantuniversumet: Everything That Can Happen Does Happen. Allen Lane. ISBN 978-1-84614-432-5
Frågor och svar
F: Vad är kvantmekanik?
S: Kvantmekanik är en gren av fysiken som förklarar hur universum fungerar på en skala som är mindre än atomer. Den kallas också för kvantfysik eller kvantteori.
F: Vad betyder termen "kvant"?
S: Termen "kvantum" kommer från latin och betyder "hur mycket". Ett energikvant är den minsta möjliga mängden (eller den minsta extra mängden), och kvantmekaniken beskriver hur denna energi rör sig eller interagerar.
F: Vad är subatomära partiklar?
S: Subatomära partiklar är partiklar som ingår i atomer, t.ex. protoner, neutroner och elektroner. De är till och med mindre än atomer.
F: Hur beskriver kvantmekaniken hur dessa partiklar fungerar?
S: Kvantmekaniken tillhandahåller matematiska regler för att studera subatomära partiklar och elektromagnetiska vågor för att förstå deras beteende och interaktioner med varandra.
F: Vad är våg-partikel-dualitet?
S: Våg-partikel-dualitet hänvisar till det faktum att både partiklar och vågor kan bete sig som varandra - de är inte två skilda enheter, utan snarare något som liknar båda kombinerade i ett fenomen.
F: Hur kan modern fysik beskrivas med hjälp av kvantmekanik?
S: Modern fysik och kemi kan förklaras genom att tillämpa kvantmekanikens matematiska regler på dem.
Sök









