Trigonometri – definition och grundläggande funktioner (sin, cos, tan)
Trigonometri — definition och grundläggande funktioner: lär dig sin, cos och tan, vinklar, trianglar och praktiska exempel för snabb förståelse.
Trigonometri (från grekiskans trigonon = tre vinklar och metron = mått) är en del av grundmatematiken som handlar om vinklar, trianglar och trigonometriska funktioner som sinus (förkortat sin), cosinus (förkortat cos) och tangent (förkortat tan). Den har en viss koppling till geometri, även om det råder oenighet om exakt vilken denna koppling är; för vissa är trigonometri bara en del av geometri.
Grundläggande definitioner
Trigonometri kan introduceras via en rätvinklig triangel. För en vinkel θ i en sådan triangel definieras de vanliga trigonometriska funktionerna som förhållanden mellan sidlängder:
- sin θ = motstående katet / hypotenusa
- cos θ = närliggande katet / hypotenusa
- tan θ = motstående katet / närliggande katet = sin θ / cos θ
Exempel: i en 3–4–5-triangel är sin(vinkel mot sidan 3) = 3/5, cos = 4/5 och tan = 3/4.
Enhetscirkeln och allmän definition
För att definiera funktionerna för alla vinklar används enhetscirkeln (cirkel med radie 1 och centrum i origo). För en vinkel θ räknat från positiva x-axeln motsvarar en punkt på enhetscirkeln (x, y) där
- cos θ = x
- sin θ = y
- tan θ = y / x (definierad när x ≠ 0)
Detta gör att trigonometriska funktioner är definierade för alla reella vinklar (i radianer) och visar deras periodiska natur.
Radianer och grader
Vinklar kan mätas i grader (°) eller i radianer. Ett helt varv är 360° = 2π rad. Inom analys och avancerad matematik används oftast radianer eftersom många formler (t.ex. gränsvärden och deriveringar) blir enklare.
Viktiga identiteter och samband
- Pythagoras-relationen: sin²θ + cos²θ = 1
- Tan i termer av sin och cos: tan θ = sin θ / cos θ
- Reciproka funktioner: sec θ = 1 / cos θ, csc θ = 1 / sin θ, cot θ = 1 / tan θ = cos θ / sin θ
- Vinkeladdition:
- sin(a ± b) = sin a cos b ± cos a sin b
- cos(a ± b) = cos a cos b ∓ sin a sin b
- Dubbla vinklar:
- sin 2a = 2 sin a cos a
- cos 2a = cos²a − sin²a = 1 − 2 sin²a = 2 cos²a − 1
Funktionsegenskaper
- Period: sin och cos har period 2π (sin(θ+2π)=sin θ). Tan har period π.
- Symmetri: cos är jämn (cos(−θ)=cos θ), sin och tan är udda (sin(−θ)=−sin θ).
- Nollställen: sin nollställs vid θ = kπ, cos vid θ = π/2 + kπ (k heltal). Tan har noll vid θ = kπ och asymptoter där cos θ = 0.
Inversa funktioner och lösning av vinklar
De inversa funktionerna arcsin, arccos och arctan används för att bestämma vinklar utifrån trigonometriska värden. Dessa definieras med begränsade värdemängder för att vara funktioner (t.ex. arcsin ger värden i [−π/2, π/2]).
Lagar för icke-rätvinkliga trianglar
För godtyckliga trianglar används två viktiga formler:
- Lagen om sinus: a / sin A = b / sin B = c / sin C
- Lagen om cosinus: c² = a² + b² − 2ab cos C (nyttig för att bestämma en sida eller vinkel när vissa andra är kända)
Derivator och gränsvärden (kort)
I analys har trigonometriska funktioner enkla derivator som ofta används:
- d/dx sin x = cos x
- d/dx cos x = −sin x
- d/dx tan x = sec² x
Gränsvärdet lim(x→0) (sin x)/x = 1 är centralt när man utgår från radianer.
Tillämpningar
Trigonometri används i många praktiska och teoretiska områden:
- Navigation och kartläggning
- Bygg- och ingenjörskonst (beräkning av höjder, lutningar och krafter)
- Fysik: svängningar, vågor, elektriska kretsar och harmoniska rörelser
- Signalbehandling och Fourieranalys
- Datagrafik och animation (rotationer, projektioner)
Tips för studier
- Lär dig enhetscirkeln och värden för vanliga vinklar (0, 30°, 45°, 60°, 90°) både i grader och radianer.
- Öva på att omskriva uttryck med identiteter (t.ex. sin²+cos²=1) för att förenkla och lösa ekvationer.
- Använd geometriska tolkningar för att få intuition (t.ex. projicera en punkt på enhetscirkeln).
Sammanfattningsvis är trigonometri ett rikt område som förbinder vinklar och längder via funktioner som sinus, cosinus och tangent. Dessa funktioner har enkla geometriska tolkningar, många algebraiska samband och breda tillämpningar i både teoretisk och tillämpad vetenskap.
Översikt och definitioner
Trigonometrin använder ett stort antal specifika ord för att beskriva delar av en triangel. Några av definitionerna inom trigonometrin är:
- Rätvinklig triangel - En rätvinklig triangel är en triangel som har en vinkel som är lika med 90 grader. (En triangel kan inte ha mer än en rätvinklig vinkel) De vanliga trigonometriska förhållandena kan bara användas på rätvinkliga trianglar.
- Hypotenusa - Hypotenusan i en triangel är den längsta sidan och den sida som är motsatt den räta vinkeln. För triangeln till höger är hypotenusan till exempel sidan c.
- Motsatsen till en vinkel - Motsatsen till en vinkel är den sida som inte skär vinkelspetsen. Till exempel är sidan a motsatsen till vinkel A i triangeln till höger.
- Angränsande sida till en vinkel - Den angränsande sidan till en vinkel är den sida som skär vinkelspetsen men som inte är hypotenusan. Till exempel är sidan b angränsande till vinkel A i triangeln till höger.
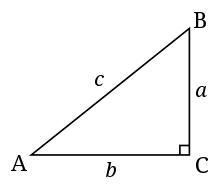
En vanlig rätvinklig triangel. C är den räta vinkeln i denna bild.
Trigonometriska förhållanden
Det finns tre huvudsakliga trigonometriska förhållanden för rätvinkliga trianglar och tre reciproka förhållanden till dessa förhållanden. Det finns totalt 6 förhållandetal. De är:
- Sinus (sin) - Sinus av en vinkel är lika med den motsatta hypotenusen {\displaystyle {{\text{Opposite}} \over {\text{Hypotenuse}}}}
- Cosinus (cos) - Cosinus av en vinkel är lika med den angränsande hypotenusen {\displaystyle {{\text{Adjacent}} \over {\text{Hypotenuse}}}}
- Tangent (tan) - Tangenten till en vinkel är lika med motsatsen till motsatsen till motsatsen {\displaystyle {{\text{Opposite}} \over {\text{Adjacent}}}}
Motsatsen till dessa förhållanden är:
Cosecant (csc) - En vinkels cosecant är lika med hypotenusan motsatt {\displaystyle {{\text{Hypotenuse}} \over {\text{Opposite}}}}
eller csc θ = 1 sin θ {\displaystyle \csc \theta ={1 \over \sin \theta }} 
Sekant (sec) - Sekanten av en vinkel är lika med hypotenusan angränsande {\displaystyle {{\text{Hypotenuse}} \over {\text{Adjacent}}}}
eller sec θ = 1 cos θ {\displaystyle \sec \theta ={1 \over \cos \theta }} 
Cotangent (cot) - En vinklas cotangent är lika med den angränsande motsatta {\displaystyle {{\text{Adjacent}} \over {\text{Opposite}}}}
eller cot θ = 1 tan θ {\displaystyle \cot \theta ={1 \over \tan \theta }} 
Eleverna använder ofta en minnesanteckning för att komma ihåg detta förhållande. Förhållandet mellan sinus, cosinus och tangent i en rätvinklig triangel kan man komma ihåg genom att föreställa dem som bokstavssträngar, till exempel SOH-CAH-TOA:
Sinus = Motsatsen ÷ Hypotenusan
Cosinus = angränsande ÷ hypotenusa
Tangent = motsatt ÷ angränsande
Användning av trigonometri
Med hjälp av sinus och cosinus kan man besvara praktiskt taget alla frågor om trianglar. Detta kallas att "lösa" triangeln. Man kan räkna ut de återstående vinklarna och sidorna i en triangel så snart man känner till två sidor och deras ingående vinkel eller två vinklar och en sida eller tre sidor. Dessa lagar är användbara inom alla grenar av geometrin, eftersom varje polygon kan beskrivas som en kombination av trianglar.
Trigonometri är också viktig för mätning, vektoranalys och studier av periodiska funktioner.
Det finns också sfärisk trigonometri, som handlar om sfärisk geometri. Den används för beräkningar inom astronomi, geodesi och navigering.
Trigonometriska lagar
Linjelagen
a Sin A = b Sin B = c Sin C {\displaystyle {{\text{a}} \over {\text{Sin A}}}}={\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}} 
Cosinuslagen
a 2 = b 2 + c 2 - 2 b c cos ( A ) {\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(A)} 
Tangenternas lag
a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ) {\displaystyle {\frac {\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}}} 
Sök