Trigonometrisk funktion
Inom matematiken är de trigonometriska funktionerna en uppsättning funktioner som relaterar vinklar till sidorna i en rätvinklig triangel. Det finns många trigonometriska funktioner, varav de tre vanligaste är sinus, cosinus och tangent, följt av kotangent, sekant och kosekant. De tre sistnämnda kallas reciproka trigonometriska funktioner eftersom de fungerar som reciproker till andra funktioner. Sekant och kosecant används sällan.
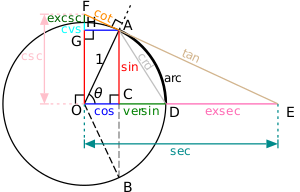
Alla trigonometriska funktioner för varje vinkel kan konstrueras med hjälp av en cirkel med centrum i O och radie 1.

Trigonometriska funktioner: Sinus , Cosinus , Tangent , Cosecant , Secant , Cotangent
Definition
De trigonometriska funktionerna kallas ibland även cirkelfunktioner. De är funktioner av en vinkel och är viktiga när man studerar trianglar, bland många andra tillämpningar. Trigonometriska funktioner definieras vanligen som förhållandet mellan två sidor i en rätvinklig triangel som innehåller vinkeln, och kan på motsvarande sätt definieras som längden på olika linjesträckor från en enhetscirkel (en cirkel som har radien ett).
Definitioner av rätvinkliga trianglar
För att definiera de trigonometriska funktionerna för vinkeln A börjar du med en rätvinklig triangel som innehåller vinkeln A:
Vi använder följande namn för sidorna i triangeln:
- Hypotenusan är den sida som är motsatt den rätvinkliga vinkeln, eller definieras som den längsta sidan i en rätvinklig triangel, i det här fallet h.
- Den motsatta sidan är den sida som är motsatt den vinkel som vi är intresserade av, i det här fallet a.
- Den angränsande sidan är den sida som är i kontakt med den vinkel vi är intresserade av och den rätvinkliga vinkeln, därav namnet. I det här fallet är den angränsande sidan b.
Alla trianglar anses existera i euklidisk geometri så att de inre vinklarna i varje triangel summerar till π radianer (eller 180°); för en rät triangel är därför de två icke-rättiga vinklarna mellan noll och π/2 radianer. Läsaren bör notera att följande definitioner, strikt sett, endast definierar de trigonometriska funktionerna för vinklar inom detta område. Vi utvidgar dem till hela uppsättningen av reella argument genom att använda enhetscirkeln, eller genom att kräva vissa symmetrier och att de ska vara periodiska funktioner.
1) Sinus av en vinkel är förhållandet mellan längden på den motsatta sidan och längden på hypotenusan. I vårt fall
sin A = motsatt hypotenusa = a h . {\displaystyle \sin A={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}}={\frac {a}{h}}. }
Observera att detta förhållande inte beror på vilken rätvinklig triangel som väljs, så länge den innehåller vinkeln A, eftersom alla dessa trianglar är likartade.
Mängden nollpunkter för sinus (dvs. de värden på x {\displaystyle x}

{ n π | n ∈ Z } . {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}. }
2) En vinkels cosinus är förhållandet mellan längden på den angränsande sidan och längden på hypotenusan. I vårt fall
cos A = intilliggande hypotenusa = b h . {\displaystyle \cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{h}}}. }
Kosinens nollor är
{ π 2 + n π | n ∈ Z } . {\displaystyle \left\{{{\frac {\pi }{2}}+n\pi {\bigg |}n\in \mathbb {Z} \right\}. }
3) Tangenten till en vinkel är förhållandet mellan längden på den motsatta sidan och längden på den intilliggande sidan. I vårt fall
tan A = motsatt intill varandra = a b . {\displaystyle \tan A={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {a}{b}}. }
Mängden nollpunkter för tangenten är
{ n π | n ∈ Z } . {\displaystyle \left\{n\pi {\big |}n\in \mathbb {Z} \right\}. }
Samma uppsättning för sinusfunktionen eftersom
tan A = sin A cos A . {\displaystyle \tan A={\frac {\sin A}{\cos A}}. }
De övriga tre funktionerna definieras bäst med hjälp av de tre ovanstående funktionerna.
4) Kosecanten csc(A) är den multiplikativa inversen av sin(A), dvs. förhållandet mellan längden på hypotenusan och längden på den motsatta sidan:
csc A = hypotenusa motsatt = h a {\displaystyle \csc A={\frac {\textrm {hypotenuse}}{\textrm {opposite}}}={\frac {h}{a}}}
5) Sekanten sec(A) är den multiplikativa inversen av cos(A), dvs. förhållandet mellan hypotenusens längd och längden på den intilliggande sidan:
sec A = hypotenusan angränsande = h b {\displaystyle \sec A={\frac {\textrm {hypotenuse}}{\textrm {adjacent}}}={\frac {h}{b}}}
6) Kotangenten cot(A) är den multiplikativa inversen av tan(A), dvs. förhållandet mellan längden på den angränsande sidan och längden på den motsatta sidan:
cot A = angränsande motsatt = b a {\displaystyle \cot A={\frac {\textrm {adjacent}}{\textrm {opposite}}}}={\frac {b}{a}}}
Definitioner med hjälp av potensserier
Man kan definiera de trigonometriska funktionerna även med hjälp av potensserier:
sin x = x - x - x 3 3 3 ! + x 5 5 ! - x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n + 1 ( 2 n + 1 ) ! {\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}
cos x = 1 - x 2 2 2 ! + x 4 4 ! - x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( - 1 ) n x 2 n ( 2 n ) ! {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}}{4!}}-{\frac {x^{6}}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
och definiera tangent, kotangent, sekant och kosekant med hjälp av identiteter, se nedan.
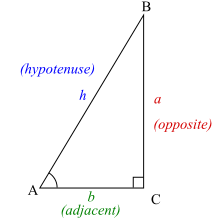
En rätvinklig triangel innehåller alltid en vinkel på 90° (π/2 radier), här markerad med C. Vinkel A och B kan variera. Trigonometriska funktioner anger förhållandet mellan sidlängder och inre vinklar i en rätvinklig triangel.
Identiteter
Några viktiga identiteter:
tan x = sin x cos x {\displaystyle \tan x={\frac {\sin x}{\cos x}}}
cot x = cos x sin x {\displaystyle \cot x={\frac {\cos x}{\sin x}}}
sec x = 1 cos x {\displaystyle \sec x={\frac {1}{\cos x}}}
csc x = 1 sin x {\displaystyle \csc x={\frac {1}{\sin x}}}
sin 2 x + cos 2 x = 1 {\displaystyle \sin ^{2}x+\cos ^{2}x=1}
sin 2 x = 2 sin x cos x {\displaystyle \sin 2x=2\sin x\cos x}
cos 2 x = cos x cos x cos x - sin x sin x = cos 2 x - sin 2 x = 2 cos 2 x - 1 = 1 - 2 sin 2 x {\displaystyle \cos 2x=\cos x\cos x\cos x-\sin x\sin x=\cos ^{2}x-\sin ^{2}x=2\cos ^{2}x-1=1-2\sin ^{2}x}}
tan 2 x = 2 tan x 1 - tan 2 x {\displaystyle \tan 2x={\frac {2\tan x}{1-\tan ^{2}x}}}}
sin ( x ± y ) = sin x cos y ± cos x sin y {\displaystyle \sin \left(x\pm y\right)=\sin x\cos y\pm \cos x\sin y}
cos ( x ± y ) = cos x cos y ∓ sin x sin y {\displaystyle \cos \left(x\pm y\right)=\cos x\cos y\mp \sin x\sin y}
tan ( x ± y ) = tan x ± tan y 1 ∓ tan x tan y {\displaystyle \tan \left(x\pm y\right)={\frac {\tan x\pm \tan y}{1\mp \tan x\tan y}}} 
Hyperboliska funktioner
De hyperboliska funktionerna liknar de trigonometriska funktionerna i det avseendet att de har mycket liknande egenskaper. De definieras i termer av exponentialfunktionen, som bygger på konstanten e.
- Hyperbolisk sinus:
sinh x = e x - e - x 2 = e 2 x - 1 2 e x = 1 - e - 2 x 2 e - x . {\displaystyle \sinh x={\frac {e^{x}-e^{-x}}}{2}}={\frac {e^{2x}-1}{2e^{x}}}={\frac {1-e^{-2x}}{2e^{-x}}}. }
- Hyperbolisk cosinus:
cosh x = e x + e - x 2 = e 2 x + 1 2 e x = 1 + e - 2 x 2 e - x . {\displaystyle \cosh x={\frac {e^{x}+e^{-x}}}{2}}={\frac {e^{2x}+1}{2e^{{x}}}={\frac {1+e^{-2x}}{2e^{-x}}}. }
- Hyperbolisk tangent:
tanh x = sinh x cosh x = e x - e - x e x + e - x = e 2 x - 1 e 2 x + 1 = 1 - e - 2 x 1 + e - 2 x . {\displaystyle \tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}={\frac {e^{2x}-1}{e^{2x}+1}}}={\frac {1-e^{-2x}}{1+e^{-2x}}}. }
- Hyperbolisk kotangent:
coth x = cosh x sinh x = e x + e - x e x - e - x = e 2 x + 1 e 2 x - 1 = 1 + e - 2 x 1 - e - 2 x , x ≠ 0. {\displaystyle \coth x={\frac {\cosh x}{\sinh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}}={\frac {e^{2x}+1}{e^{2x}-1}}}={\frac {1+e^{-2x}}}{1-e^{-2x}}},\qquad x\neq 0.}
- Hyperbolisk sekant:
sech x = 1 cosh x = 2 e x + e - x = 2 e x e 2 x + 1 = 2 e - x 1 + e - 2 x . {\displaystyle \operatorname {sech} \,x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}}={\frac {2e^{{x}}}{e^{2x}+1}}={\frac {2e^{-x}}{1+e^{-2x}}}}. }
- Hyperbolisk kosecant:
csch x = 1 sinh x = 2 e x - e - x = 2 e x e 2 x - 1 = 2 e - x 1 - e - 2 x , x ≠ 0. {\displaystyle \operatorname {csch} \,x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}={\frac {2e^{x}}}{e^{2x}}-1}}={\frac {2e^{-x}}{1-e^{-2x}}}},\qquad x\neq 0.} 
Relaterade sidor
Sök






















