Bernoullis princip: Förklaring, formel och exempel inom strömningsdynamik
Bernoullis princip: tydlig förklaring, formel och praktiska exempel inom strömningsdynamik — förstå hur tryck, hastighet och energibalans hänger ihop.
Bernoullis princip är en idé från strömningsdynamiken. Den säger att trycket minskar när vätskans hastighet ökar. Bilden till höger visar att detta sker. Luften i den breda delen av röret har ett högre statiskt tryck än den tunna delen. För ett jämnt flöde måste mängden vätska som kommer in i röret vara lika stor som mängden som lämnar röret, så vätskehastigheten i den tunna delen måste öka.
När en kraft verkar över en yta kallas den för "tryck". Ett högre tryck pressar (accelererar) en vätska mot ett lägre tryck. Så varje förändring av en vätskas hastighet måste motsvaras av en förändring av trycket (kraften). Bernoulli såg att medan vätskan rörde sig snabbare i den mindre delen av röret blev trycket lägre. Observera att detta avser förändringar i hastighet och tryck längs en enda flödesväg och inte gäller för två olika flöden med olika hastigheter.
Den fullständiga versionen av Bernoullis princip omfattar både det arbete som utförs av trycket och av förändringarna i potentiell energi från höjdförändringar. I denna form säger principen att summan av trycket, den kinetiska energin och den potentiella energin är en konstant. (Bernoulli tar inte hänsyn till viskositet eller kompressibilitet).
Formel och centrala termer
För ett stationärt (icke-tidsberoende), inkompressibelt och icke-visköst flöde längs en strömlinje kan Bernoullis ekvation skrivas som:
p + ½ρv² + ρgh = konstant
Här är:
- p = statiskt tryck (Pa)
- ρ = densitet (kg/m³)
- v = flödeshastighet (m/s)
- g = tyngdaccelerationen (≈9,81 m/s²)
- h = höjden över ett referensplan (m)
Termen ½ρv² kallas ofta dynamiskt tryck, och summan p + ½ρv² kallas stagnationstryck (eller totaltryck om man även räknar med ρgh för höjdskillnader).
Antaganden och begränsningar
- Flödet måste vara stationärt (konstant över tiden) för formen ovan.
- Följande effekter försummas i grundformen: viskositet (friktion), kompressibilitet (vid höga hastigheter eller gaser med stora densitetsändringar), värme- och arbeteöverföring, samt energitillskott eller -förluster från pumpar och turbiner.
- Bernoullis ekvation gäller längs samma strömlinje eller mellan punkter där samma energilinje gäller; man kan inte utan vidare jämföra två oberoende flöden.
- Vid reella rörledningar och kanaler måste man ofta lägga till ett hufvudförlust-led (head loss) för att kompensera för viskösa förluster.
Exempel — räkneexempel i en rörkontraktion
Antag vatten (ρ ≈ 1000 kg/m³) i ett rör där en bred sektion har area A1 = 0,05 m² och hastigheten v1 = 1,0 m/s. I en smalare sektion är arean A2 = 0,02 m². Kontinuitet (A1v1 = A2v2) ger flödet Q = 0,05 m³/s och
v2 = Q / A2 = 0,05 / 0,02 = 2,5 m/s.
Om höjden är densamma kan Bernoulli mellan punkterna skrivas som p1 + ½ρv1² = p2 + ½ρv2², vilket ger
p2 − p1 = ½ρ(v1² − v2²) = 0,5·1000·(1,0² − 2,5²) = −2625 Pa.
Alltså är det statiska trycket i den smalare sektionen cirka 2625 Pa lägre än i den bredare sektionen (om inga förluster förekommer).
Tillämpningar
- Venturi-mätare och andra flödesmätare bygger på tryckskillnad vid variation i area.
- Flygplansvingar: högre hastighet över vingens över- resp. undersida ger tryckskillnad som genererar lyft.
- Karburetorer, sug i munstycken och många pneumatiska system utnyttjar principen.
- Hydraulik och rörsystemsdimensionering där tryckfall och hastigheter behöver beräknas (med tillägg för friktion).
Vidare kommentarer
Bernoullis princip förklarar hur energi omfördelas mellan tryck, rörelseenergi och lägesenergi i flödet. För exakt ingenjörsberäkning måste man ofta komplettera med förluster (t.ex. Darcy–Weisbach för rörfriktion) eller använda kompressibla flödestermodeller och energiekvationer vid höga hastigheter i gaser. Trots sina begränsningar är Bernoullis princip ett mycket användbart och intuitivt verktyg för att förstå och uppskatta sambandet mellan hastighet och tryck i många praktiska situationer.
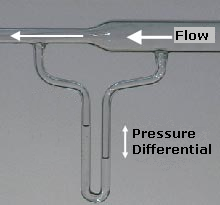
En venturi som visar Bernoullis princip. Vattnet till höger är lägre på grund av det högre trycket i det stora röret.
Frågor och svar
Fråga: Vad är Bernoullis princip?
S: Bernoullis princip är ett flödesdynamiskt begrepp som säger att trycket minskar när en vätskas hastighet ökar.
F: Hur demonstreras Bernoullis princip i fotot till höger?
S: Fotot visar att luften i den breda delen av röret har ett högre statiskt tryck än den tunna delen, vilket gör att fluidens hastighet i den tunna delen ökar.
F: Vad är tryck?
S: Tryck är en kraft som verkar över en yta.
F: Vad händer när en vätskas hastighet ändras?
S: En förändring av en vätskas hastighet måste motsvaras av en förändring av trycket eller kraften.
F: Gäller Bernoullis princip för två olika flöden med olika hastigheter?
S: Nej, Bernoullis princip gäller endast för förändringar i hastighet och tryck längs en enda flödesväg.
F: Vad omfattar den fullständiga versionen av Bernoullis princip?
S: Den fullständiga versionen av Bernoulliprincipen omfattar både det arbete som utförs av trycket och av förändringarna i potentiell energi från höjdförändringar.
F: Vad tar Bernoulliprincipen inte hänsyn till?
S: Bernoullis princip tar inte hänsyn till viskositet eller kompressibilitet.
Sök