Binärt talsystem (bas 2) – definition, exempel och användning i datorer

Lär dig binärt talsystem (bas 2): definition, omvandlingsexempel och hur datorer använder 0 och 1 för att representera text, ljud och bild — en enkel guide för nybörjare.

Författare: Leandro Alegsa

14-01-2026 23:12

Binärt är ett talsystem med bas 2. Det kallas bas 2 eftersom det bara använder två olika siffror: 0 och 1. I motsats till det vanliga decimalsystemet (bas 10), som använder tio tecken (0–9), bygger det binära systemet på potenser av 2. När binära tal skrivs anges det ofta med ett subscript "(2)" eller med prefixet "0b" för att skilja dem från tal i bas 10, till exempel 1101(2) eller 0b1101.

Datorer arbetar binärt eftersom elektroniska kretsar och ledningar enkelt kan representera två tillstånd — till exempel ström på/av, hög/låg spänning eller 1/0. Genom att kombinera många binära enheter kan datorer representera och bearbeta all slags information: text, ljud, bilder och video.

Platsvärde och omvandling mellan decimal och binärt

I det binära systemet bestäms varje positions värde av potenser av 2. Från höger till vänster representerar positionerna 2^0, 2^1, 2^2, 2^3 osv. Ett binärt tal tolkas genom att summera de potenser där siffran är 1.

Exempel (decimal till binärt):

Decimal 13 = 8 + 4 + 1 = 2^3 + 2^2 + 2^0 → binärt: 1101(2).
Decimal 29 = 16 + 8 + 4 + 1 = 2^4 + 2^3 + 2^2 + 2^0 → binärt: 11101(2).

Vanlig metod (divisionsmetoden) för att omvandla ett decimaltal till binärt: dividera talet med 2, skriv ned resten (0 eller 1), fortsätt med kvoten tills kvoten är 0. Restvärdena läses baklänges och bildar det binära talet.

Grundläggande räkning och begrepp

Bit — minsta informationsenheten, antingen 0 eller 1.
Byte — normalt 8 bitar. En byte kan representera 256 olika värden (0–255).
Binär addition följer samma idéer som decimalsystemet, men med bas 2: 0+0=0, 0+1=1, 1+1=10 (0 med överföring 1).

Exempel på binär addition:

1011 (11 decimal)
+ 0101 (5 decimal)
=10000 (16 decimal)

Hur binärt används i datorer

Binära tal används i flera lager i en dator:

På kretsnivå representeras bitar av transistorer som är av/på eller av kondensatorer i minnesceller.
Logiska grindar (AND, OR, NOT, XOR) arbetar med binära värden för att utföra beräkningar och beslut.
Högre nivåer använder grupper av bitar för att representera tal, tecken och multimediainnehåll. Till exempel i ASCII är bokstaven "A" representerad som decimal 65 = binärt 01000001.
Filer och protokoll kodar data i bit- och byte-sekvenser; processorers register och bussar är ofta 8, 16, 32 eller 64 bitar långa.

Praktiska notationer och tips

Binära tal skrivs ibland med subscript (2): 1010(2) eller med prefixet 0b: 0b1010.
För långa binära tal används ofta hexadecimal (bas 16) som kompakt representation — varje hexsiffra motsvarar fyra binära bitar.
För att snabbt uppskatta storlekar: 1 byte ≈ 8 bitar, 1 kilobyte (KB) ≈ 1024 byte, 1 megabyte (MB) ≈ 1024 KB.

Sammanfattningsvis är det binära talsystemet enkelt i grund — bara två symboler — men kraftfullt i praktiken eftersom det passar perfekt ihop med elektroniska kretsars två tillstånd. Genom att kombinera många bitar kan man representera komplex information och utföra avancerade beräkningar i dagens datorer.

System med nummer

När du introduceras till binära tal är det bra att gå tillbaka och tänka på hur bas 10- eller decimaltal fungerar. Tänk på talet 1101₍₁₀₎ (bas 10). Vi identifierar det här talet som ett tusen, ett hundra, ett eftersom det har en 1 på tusenplatsen, en 1 på hundratalsplatsen och en 1 på ettorsplatsen. Men eftersom platserna representerar 8, 4, 2 och 1 i binärt tal i stället för 1000, 100, 10 och 1, skulle värdet omräknat till decimal (bas 10) vara 8 + 4 + 1 = 13₍₁₀₎ .

Ett annat exempel är det binära talet 101₍₂₎ som är 5 i decimal. Biten till höger är 1 och har värdet 1 (2^0). Den mittersta biten har värdet 2 (2^1 eller bara 2), men den är en 0, så den adderas inte. Biten till vänster är 1 och har värdet 4 (2^2 eller 2 * 2). De bitar som är 1:or har värdena 1 och 4. 1 + 4 = 5.

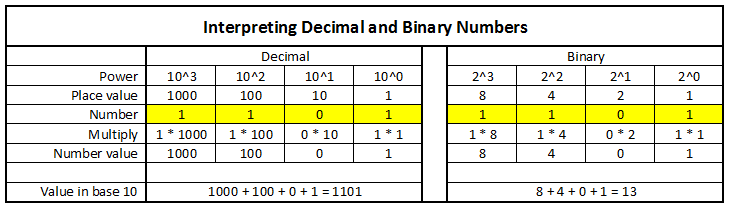
Hur decimala och binära tal tolkas

Datorer

Alla datorer använder binär kod på lägsta nivå. De flesta hårddiskar, som cd-skivor och dvd-skivor, använder binär för att representera stora filer.

I datorer kallas åtta binära bitar tillsammans för en byte. Storleken på filer mäts vanligen i kilobyte eller megabyte (ibland i gigabyte). En kilobyte är 1 000 bytes. En megabyte är 1000 kilobyte, en gigabyte är 1000 megabyte och en terabyte är 1000 gigabyte. Ibland är det lättare att mäta bytes i grupper om 1024, eftersom 1024 är en potens av 2. Det finns 1024 bytes i en kibibyte, 1024 kibibibyte i en mebibyte och 1024 mebibyte i en gibibyte.

Frågor och svar

F: Vad är binär?

S: Binärt är ett bas 2-talsystem som använder två möjliga tal: 0 och 1.

F: Varför är binärt ett bas 2-system?

S: Binär är ett bas 2-system eftersom det använder två möjliga tal: 0 och 1.

F: Vad är skillnaden mellan binär och decimal?

S: Binär är ett bas 2-system och använder två möjliga tal, medan decimal är ett bas 10-system och använder tio tecken (0-9).

F: Varför arbetar datorer binärt?

S: Datorer arbetar binärt eftersom ledningar kan lagra information på två olika sätt: genom att vara strömförande eller inte strömförande.

F: Hur kan binära tal användas?

S: Uppsättningar av binära tal kan användas för att representera vilken information som helst, t.ex. text, ljud eller video.

F: Hur skiljer sig binära tal från decimala tal?

S: Binära tal skiljer sig från decimala tal genom att man lägger till ett index "(2)" när de skrivs.

F: Vilka tecken används i det decimala talsystemet?

S: Det decimala talsystemet använder tio tecken: 0-9.

Sök