Fourierserier – definition, Fourieranalys och tillämpningar
Fourierserier och Fourieranalys: tydlig definition och praktiska tillämpningar inom signalbehandling, fysik och ingenjörsvetenskap — från teori till verkliga exempel.
Joseph Fourier sade att det är möjligt att använda sinusvågor för att approximera en annan funktion. Detta är en serie i matematisk mening. Denna teori kan generaliseras till Fouriertransformationen. Matematisk analys av dessa funktioner kallas Fourieranalys.
Redan på 1700-talet använde matematiker som Euler, Lagrange och Bernoulli sinusoider för att approximera och modellera andra funktioner. När Fourier publicerade ett arbete om värme 1822 sade han att sådana approximationer existerar för alla sådana funktioner (som är kontinuerliga i intervallet). Till en början trodde folk inte på honom, och det tog nästan tio år innan ett bevis (för en del av problemet) dök upp.
I dag används fourierserier mycket inom digital signalbehandling.
Vad är en fourierserie?
En fourierserie är en representation av en periodisk funktion som en summa av enkla sinus- och cosinusvågor (harmoniska frekvenser). För en funktion med period 2π skrivs den vanligtvis som
f(x) ≈ a0/2 + Σ_{n=1}^∞ [a_n cos(nx) + b_n sin(nx)],
där koefficienterna a_n och b_n bestäms av integraler över ett periodintervall:
a_n = (1/π) ∫_{-π}^{π} f(x) cos(nx) dx, b_n = (1/π) ∫_{-π}^{π} f(x) sin(nx) dx, a0 = (1/π) ∫_{-π}^{π} f(x) dx.
Det finns också en komplex form av fourierserien som använder exponentiella termer e^{inx}:
f(x) ≈ Σ_{n=-∞}^{∞} c_n e^{inx}, där c_n = (1/2π) ∫_{-π}^{π} f(x) e^{-inx} dx.
Varför fungerar det?
Nyckeln är ortogonalitet: funktionerna cos(nx) och sin(nx) för olika n är ortogonala på intervallet, vilket gör att man kan projicera f på varje komponent och beräkna koefficienterna unikt. Fourierserier bryter alltså ner en komplex periodisk signal i enkla frekvenskomponenter (amplitud och fas).
Konvergens och begränsningar
Att en fourierserie verkligen konvergerar mot funktionen beror på funktionens egenskaper. Klassiska tillräckliga villkor kallas Dirichlets villkor — bland annat krävs att funktionen har ett ändligt antal maxima, minima och diskontinuiteter på en period. Fler avancerade resultat gavs senare av Riemann och Lebesgue.
Vid diskontinuiteter konvergerar serien vanligtvis mot medelvärdet av gränsvärdena från vänster och höger. Ett välkänt fenomen är Gibbs-fenomenet: nära en hoppdiskontinuitet uppträder en oscillation/överskjutning som inte försvinner helt när antalet termer ökar, även om oscillationens bredd blir mindre.
Anslutning till Fouriertransformationen
Fourierserier gäller för periodiska funktioner. När perioden går mot oändligheten övergår fourierserien i Fouriertransformationen, vilken används för icke-periodiska signaler och ger ett kontinuerligt spektrum av frekvenser. Båda verktygen tillhör området Fourieranalys och har gemensamma satser som Parsevals och Plancherels satser som kopplar energin i tidsdomänen till energin i frekvensdomänen.
Exempel och tolkning
Ett konkret exempel är en fyrkantvåg: dess fourierserie innehåller endast udda harmoniska (sinus- eller cosinustermer med frekvenser n = 1, 3, 5, ...) och amplituder som faller som 1/n. Detta förklarar varför en fyrkantig tidssignal kan återskapas genom att lägga ihop ett fåtal sinuskomponenter.
Tillämpningar
- Signalbehandling: spektralanalys, filtrering, moduleringssystem och brusreducering.
- Bild- och ljudkompression: metoder som JPEG (använder liknande diskret kosinus-transform) och MP3 bygger på att representera data i ett frekvensbaserat system för effektiv kodning.
- Lösning av differentialekvationer: Fourierserier används för att lösa PDE, särskilt värme- och vågekvationer — detta var också Fouriers ursprungliga motiv i arbetet om värme.
- Elektronik och kommunikation: analys av kretsers frekvenssvar, antenndesign och spektrumanalys.
- Vetenskaplig analys: spektralanalys i fysik, kemi (spektroskopi) och ekonomi (frekvenskomponenter i tidsserier).
- Numerisk beräkning: snabba algoritmer som FFT (Fast Fourier Transform) gör det praktiskt möjligt att snabbt beräkna diskreta fouriertransformer för stora datamängder.
Historisk avslutning
Fouriers idéer utvecklades och formaliserades efter hans tid. Matematiker som Dirichlet, Riemann och senare Lebesgue gav rigorösa villkor för konvergens och integrerbarhet. Idag utgör fourierserier och transformer en central del av både teoretisk och tillämpad matematik.
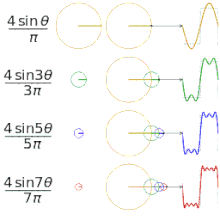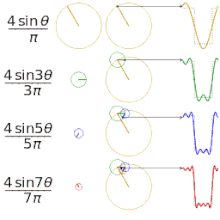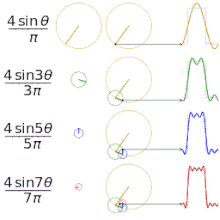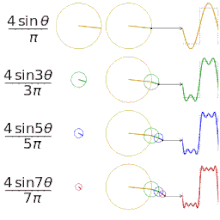
Approximering av olika "kvadratiska" funktioner med hjälp av fourierserier
Frågor och svar
F: Vem var Joseph Fourier?
S: Joseph Fourier var en fransk matematiker som föreslog att sinusvågor kan användas för att approximera en annan funktion.
F: Vad är en Fourier-serie?
S: En Fourier-serie är en serie som använder sinusvågor för att approximera en annan funktion.
F: Vad är Fouriertransformen?
S: Fouriertransformen är en generalisering av den teori som använder sinusvågor för att approximera en annan funktion.
F: Vad är Fourieranalys?
S: Fourieranalys är en matematisk analys av de funktioner som använder sinusvågor för att approximera en annan funktion.
F: Vem använde sinuskurvor för att approximera och modellera andra funktioner på 1700-talet?
S: Matematiker som Euler, Lagrange och Bernoulli använde sinuskurvor för att approximera och modellera andra funktioner under 1700-talet.
F: Vad föreslog Fourier i sitt arbete om värme 1822?
S: I sitt arbete om värme 1822 föreslog Fourier att sådana approximationer med hjälp av sinusvågor finns för alla kontinuerliga funktioner i ett givet intervall.
F: Hur används Fourier-serier inom digital signalbehandling?
S: Fourierserier används ofta inom digital signalbehandling för att approximera och analysera signaler.
Sök