Fouriertransform | matematisk funktion som kan användas för att hitta de basfrekvenser som en våg består av

Fouriertransformen är en matematisk funktion som kan användas för att hitta de basfrekvenser som en våg består av. Föreställ dig att du spelar ett ackord på ett piano. När det spelas blandas ljuden från ackordets toner ihop och bildar en ljudvåg. Detta fungerar därför att var och en av de olika tonernas vågor interfererar med varandra genom att adderas eller upphävas vid olika punkter i vågen. En Fouriertransform tar denna komplexa våg och kan hitta de frekvenser som den består av, vilket innebär att den kan hitta de toner som ett ackord består av.

Utgången av en Fouriertransform kallas ibland för ett frekvensspektrum eller en frekvensfördelning eftersom den visar en fördelning av möjliga frekvenser för inmatningen. Denna funktion har många användningsområden inom kryptografi, oceanografi, maskininlärning, radiologi, kvantfysik samt ljuddesign och visualisering.

Fouriertransformen av en funktion f ( x ) {\displaystyle f(x)} f(x) , ibland skriven som F { f } {\displaystyle {\mathcal {F}}}\{f\}} ${\mathcal {F}}\{f\}$ , ges genom

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}\,dx} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}\,dx$

där:

α {\displaystyle \alpha } $\alpha$ är en frekvens.
F ( α ) {\displaystyle F(\alpha )} $F(\alpha )$ är Fouriertransformationsfunktionen och returnerar ett värde som anger hur stor frekvens α {\displaystyle \alpha } $\alpha$ är i den ursprungliga signalen.
e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} $e^{-2\pi i\alpha x}$ representerar att den ingående vågfunktionen f ( x ) {\displaystyle f(x)} lindas runt ursprunget i det komplexa planet vid en viss frekvens α {\displaystyle \alpha } $\alpha$ .

Den omvända Fouriertransformen ges av

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }\,d\alpha } $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }\,d\alpha$

En Fouriertransform visar vilka frekvenser som finns i en signal. Tänk till exempel på en ljudvåg som innehåller tre olika musikaliska toner: A, B och C. Om man gör en graf över Fouriertransformen av denna ljudvåg (med frekvensen på x-axeln och intensiteten på y-axeln) kommer man att se en topp vid varje frekvens som motsvarar en av musiknoterna.

Många signaler kan skapas genom att addera cosinus och sinus med olika amplitud och frekvens. Fouriertransformen visar amplituderna och faserna för dessa cosinus och sinus mot deras respektive frekvenser.

Fouriertransformationer är viktiga eftersom många signaler blir mer begripliga när deras frekvenser separeras. I ljudexemplet ovan är det inte uppenbart att noterna A, B och C finns i signalen om man tittar på signalen i förhållande till tiden. Många system gör olika saker med olika frekvenser, så dessa typer av system kan beskrivas genom vad de gör med varje frekvens. Ett exempel på detta är ett filter som blockerar höga frekvenser.

Att beräkna en Fouriertransform kräver förståelse för integration och imaginära tal. Datorer används vanligen för att beräkna Fouriertransformationer av allt utom de enklaste signalerna. Fast Fourier Transform är en metod som datorer använder för att snabbt beräkna en Fouriertransform.

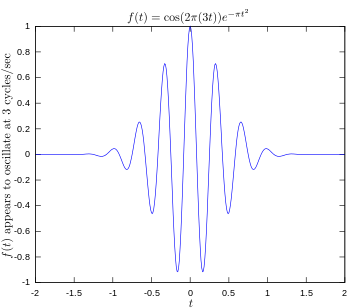
· Original function showing a signal oscillating at 3 hertz.

Originalfunktion som visar en signal som oscillerar med 3 hertz.

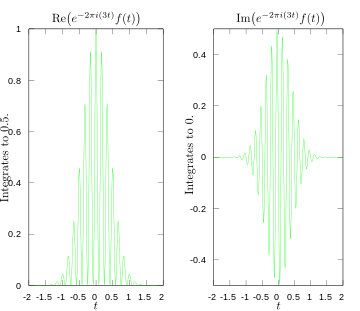
· Real and imaginary parts of integrand for Fourier transform at 3 hertz

Real och imaginär del av integrand för Fouriertransform vid 3 hertz

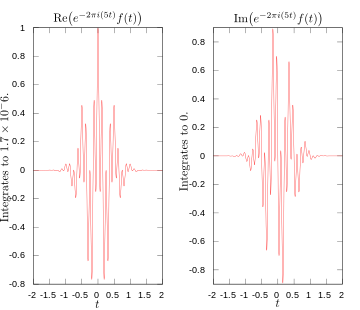
· Real and imaginary parts of integrand for Fourier transform at 5 hertz

Real och imaginär del av integrand för Fouriertransform vid 5 hertz

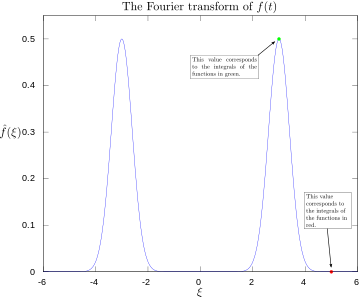
· Fourier transform with 3 and 5 hertz labeled.

Fouriertransform med 3 och 5 hertz markerade.

Relaterade sidor

Fourieranalys
Satsen om Fourier-inversion
Fourierserier
Laplace-transformation

Frågor och svar

Fråga: Vad är Fouriertransformationen?

S: Fouriertransformen är en matematisk funktion som kan användas för att hitta de basfrekvenser som en våg består av. Den tar en komplex våg och hittar de frekvenser som den består av, vilket gör det möjligt att identifiera de toner som ingår i ett ackord.

F: Vilka är några användningsområden för Fouriertransformen?

S: Fouriertransformen har många användningsområden inom kryptografi, oceanografi, maskininlärning, radiologi, kvantfysik samt ljuddesign och visualisering.

F: Hur beräknas Fouriertransformen?

S: Fouriertransformen av en funktion f(x) ges av F(ב) = ∫-∞+∞f(x)e-2נiבxdx där ב är en frekvens. Detta returnerar ett värde som representerar hur utbredd frekvensen ב är i den ursprungliga signalen. Den omvända Fouriertransformen ges av f(x) = ∫-∞+∞F(ב)e+2נixבdב.

F: Hur ser resultatet av en Fouriertransform ut?

S: Ett resultat av en Fouriertransform kan kallas antingen ett frekvensspektrum eller en fördelning, eftersom det visar en fördelning av möjliga frekvenser för inmatningen.

Fråga: Hur beräknar datorer snabba Fouriertransformationer?

S: Datorer använder en algoritm som kallas Fast Fourier Transform (FFT) för att snabbt beräkna alla utom de enklaste signalernas transformationer.

F: Vad visar inte att titta på signaler med avseende på tid?

S: Att titta på signaler med avseende på tid gör det inte uppenbart vilka toner som finns i dem; många signaler blir mer begripliga när deras frekvenser separeras och analyseras individuellt i stället.