Elektrisk impedans — definition, formler och frekvensberoende

Lär dig elektrisk impedans: definition, tydliga formler för resistans, induktans och kapacitans samt hur impedansen varierar med frekvens. Exempel och beräkningar.

Författare: Leandro Alegsa

24-09-2025 12:39

Elektrisk impedans är den totala motståndskraften en elektrisk krets uppvisar mot ström- eller spänningsändringar, särskilt vid växelström. Impedans tar hänsyn både till det rena motståndet (som omvandlar elektrisk energi till värme) och till reaktiva komponenter (som lagrar energi i elektriska eller magnetiska fält).

De två vanligaste sätten att beskriva en impedans är (se den andra figuren, "komplext impedansplan"):

i rektangulär form med motståndet "R" (reell del) och reaktansen "X" (imaginär del), till exempel Z = 1 + 1 j {\displaystyle Z=1+1j} $Z=1+1j$
i polär form med en magnitud och en fas (storleken | Z | {\displaystyle \left\vert Z\right\vert } $\left\vert Z\right\vert$ och vinkeln {\displaystyle \angle \theta } $\angle \theta$ ) — till exempel Z = 1,4 ∠ 45 ∘ $Z=1.4\angle 45^{\circ }$ (1,4 Ω vid 45°)

Skillnad mellan motstånd och impedans

Impedans och motstånd är besläktade men inte identiska. Ett rent motstånd (resistans) motstår all ström genom sig och omvandlar elektrisk energi till värme. Ohms lag för ett rent motstånd skrivs som:

V = R ∗ I {\displaystyle V=R*I} $V=R*I$ , där V är spänningen, R är motståndet och I är strömmen.

Impedans beskriver istället hur en komponent reagerar på förändringar i spänning eller ström vid olika frekvenser. Induktorer motstår snabba förändringar i ström (genom att skapa ett magnetfält) medan kondensatorer motstår snabba förändringar i spänning (genom att skapa ett elektriskt fält). Det är därför lämpligt att tala om frekvensberoendet hos impedans.

Frekvensberoende – induktans och kapacitans

Impedansen för en ideal induktor och en ideal kondensator ges av följande formler:

För induktorn: Z = j 2 π f L {\displaystyle Z=j2\pi fL\\,} $Z=j2\pi fL\,$

För kondensatorn: Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}}} $Z={\frac {1}{j2\pi fC}}$

Där Z är impedansen, j är den imaginära enheten ({\displaystyle {\sqrt {-1}}} ${\sqrt {-1}}$ — ingenjörers standard istället för i), π {\displaystyle \pi } $\pi$ är pi, f är frekvensen i hertz, L är induktansen och C är kapacitansen. Enheterna för motstånd och impedans är desamma: ohm (Ω) {\displaystyle \Omega } $\Omega$ .

Detta leder till enkla gränsfall:

Vid f = 0 Hz (likström) har en ideal induktor Z = 0 (kortslutning) medan en ideal kondensator har Z → ∞ (öppen krets).
Vid mycket höga frekvenser blir en induktors impedans stor (den blockerar snabba växlingar) medan en kondensators impedans blir liten (den leder lätt snabba växlingar).

Reaktans, fas och uttryck i rektangulär/polär form

Reaktansen X är den imaginära delen av impedansen: Z = R + jX. För en induktor är X_L = ωL = 2πfL (positiv), för en kondensator är X_C = −1/(ωC) (negativ). I polär form anges impedansen som magnitud |Z| och fasvinkel θ, där θ = arctan(X/R). Fasvinkeln visar hur mycket strömmen ligger efter (eller före) spänningen.

Ohm:s lag för växelström och phasorer

För växelström gäller samma grundläggande samband men med komplexa storheter: V = Z ∗ I {\displaystyle V=Z*I} $V=Z*I$ , där V och I kan vara fasorer (komplexa värden som representerar amplitud och fas). Genom att använda phasorer kan sinussignaler behandlas som komplexa konstanter vid en given frekvens, vilket gör kretsanalys enklare.

Energi, effekt och reaktiv effekt

Ett viktigt praktiskt resultat är att endast den reella delen av impedansen (R) förbrukar aktiv effekt (omvandlar den till värme). Induktorer och kondensatorer lagrar energi växelvis i magnetfält respektive elektriskt fält och levererar ofta tillbaka denna energi till kretsen — detta ger reaktiv effekt (Q). I phasorform uttrycks komplex effekt som S = V I* (vid RMS-värden), där realdelen är aktiv effekt P och imaginärdelen är reaktiv effekt Q.

Seriekoppling, parallellkoppling och transformering

Precis som för motstånd kan impedanser kombineras i serie och parallellt:

Seriekopplade impedanser adderas: Z_tot = Z1 + Z2 + ...
Parallellkopplade impedanser adderas som inverser: 1/Z_tot = 1/Z1 + 1/Z2 + ...

Vid analys används ofta komplex algebra eller impedansdiagram för att beräkna nätverkens beteende över frekvens.

Impedansanpassning och reflektioner

Om impedansen hos källan, ledningen och belastningen inte matchar reflekteras en del av signalen tillbaka mot källan, vilket kan ge förluster och störningar. Reflektionskoefficienten beräknas med följande formel:

Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}}} $\Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}$ där Γ {\displaystyle \Gamma } $\Gamma$ är reflektionskoefficienten, Z_{S} $Z_{S}$ är källans impedans och Z_{L} $Z_{L}$ är belastningens impedans.

För maximal effektöverföring i en linje bör belastningens impedans vara den komplexa konjugaten till källans impedans (Z_L = Z_S*). I praktiken används impedansanpassning, transformatorer eller matchningsnätverk för att minimera reflektioner (se även begreppet VSWR — stående vågförhållande).

Vågers impedans

Alla medier som kan föra en våg har en karakteristisk vågimpedans. Till exempel har vakuum (tomt utrymme) en impedans på cirka 377 Ω {\displaystyle \Omega } $\Omega$ , vilket är relevant för elektromagnetiska vågor såsom ljus.

Praktiska kommentarer

Vid mätningar används ofta nätverksanalysatorer och impedansmätare för att bestämma Z(f) över ett frekvensområde.
I reala komponenter finns även förluster: en induktor har ofta både L och ett inre R (serie- eller parallellkomponent), och en kondensator kan ha läckströmmar och ESR (ekvivalent serieresistans).
Signaler uppbyggda av flera frekvenser (se Fouriertransformen) påverkas av impedansens frekvensberoende: olika frekvenskomponenter ser olika impedanser och dämpas/förstärks olika.

På det fysiska planet kan man förenklat säga att:

Motstånd orsakas av elektronernas kollisioner med atomer i ledaren.
En kondensators impedans beror på att ett elektriskt fält byggs upp mellan dess plattor.
En induktors impedans beror på att ett magnetfält byggs upp kring ledaren.

Sammanfattningsvis är impedans ett grundläggande begrepp i växelströmsanalys och signalöverföring: det beskriver hur olika kretsdelar påverkar amplitud och fas hos ström och spänning och varierar i allmänhet med frekvens.

En signal reflekteras delvis tillbaka där impedansen förändras.

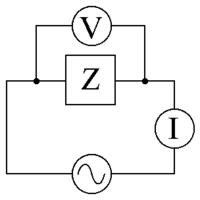
En växelströmsförsörjning med en spänning V {\displaystyle \scriptstyle V} $\scriptstyle V$ över en impedans Z {\displaystyle \scriptstyle Z} , som $\scriptstyle Z$ driver en ström I {\displaystyle \scriptstyle I} $\scriptstyle I$ .

En grafisk representation av det komplexa impedansplanet.

Fas

Över ett motstånd går både spänningen och strömmen upp och ner samtidigt, de sägs vara i fas, men med en impedans är det annorlunda, spänningen är förskjuten med 1/4 våglängd bakom strömmen i en kondensator och framåt i en induktor.

En 1/4 våglängd representeras vanligen av det imaginära talet "j", vilket också motsvarar en 90 graders förskjutning.

Användningen av det imaginära talet "j" gör matematiken mycket enklare och gör det möjligt att beräkna den totala impedansen på samma sätt som med motstånd, t.ex. är ett motstånd plus en impedans i serie R+Z och i parallell är det (R*Z)/(R+Z).

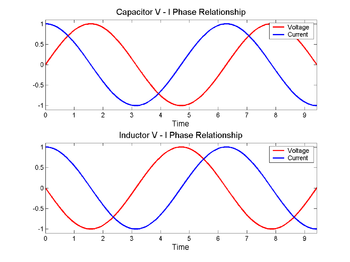
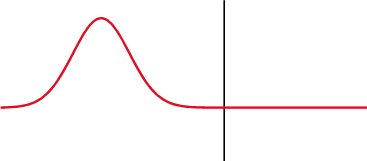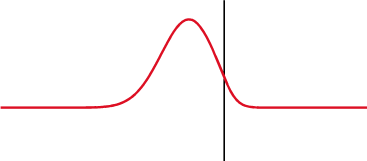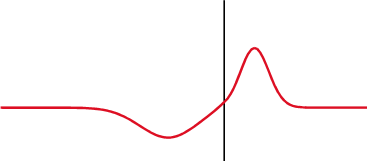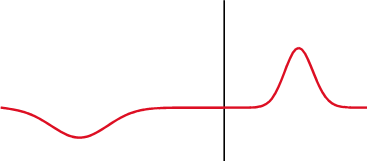
Över en kondensator (överst) ändras spänningen (röd) efter strömmen (blå), över en induktor (nederst) ändras den före. Fasskillnaden mellan spänningen och strömmen är 1/4 våglängd.

Frågor och svar

F: Vad är elektrisk impedans?

S: Elektrisk impedans är den mängd motstånd som en krets utgör mot ström- eller spänningsförändringar.

F: Hur kan elektrisk impedans skrivas?

S: Elektrisk impedans kan skrivas med motståndet "R" (reell del) och reaktansen "X" (imaginär del), samt med magnitud, fas, storlek och vinkel.

F: Vad är skillnaden mellan motstånd och impedans?

S: Den viktigaste skillnaden mellan motstånd och impedans är ordet "förändring"; med andra ord påverkar förändringshastigheten impedansen. Motstånd motstår all ström som går genom det, medan en induktor motstår förändringar i strömmen och en kondensator motstår förändringar i spänningen.

F: Vilka formler finns för motstånd och impedans?

S: För motstånd gäller V=R*I där V är spänning, R är motstånd och I är ström; för induktorer gäller Z=j2πfL; för kondensatorer gäller Z=1/j2πfC; där Z representerar impedans, j representerar det imaginära talet -1 , π representerar konstant pi, f representerar frekvens, L representerar induktans, C representerar kapacitans.

F: Vilka är några fysiska förklaringar till motstånd kontra impedans?

S: Motstånd orsakas av att elektroner kolliderar med atomer i motstånd, medan en induktans impedans kommer från skapandet av ett elektriskt fält och en kondensators från skapandet av ett magnetfält. Dessutom förslösar motstånd energi medan induktorer och kondensatorer lagrar energi som sedan kan återföras till källan när den går ner.

F: Hur beräknar man reflektionskoefficienten?

S: Reflektionskoefficienten kan beräknas med hjälp av Γ=(ZL-ZS)/(ZL+ZS) där Γ (gamma) står för reflektionskoefficienten, ZS står för källans impedans och ZL står för belastningens impedans.

Sök