Fraktal

Exempel

Det finns många olika typer av fraktaler, och de är gjorda på många olika sätt. Ett exempel är Sierpinski-triangeln, där det finns ett oändligt antal små trianglar inuti den stora triangeln. Ett annat exempel är Mandelbrot-mängden, som är uppkallad efter Benoît Mandelbrot. Sierpinksi-triangeln är konstruerad med hjälp av mönster, men Mandelbrot-mängden bygger på en ekvation.

Det finns också många naturliga exempel på fraktaler i naturen, bland annat träd, snöflingor, vissa grönsaker och kustlinjer.

Koch-kurvan

Koch-kurvan är ett enkelt exempel på en fraktal. Börja med en del av en rak linje - ett segment av en rak linje. Skär linjen i tre lika stora bitar. Gör dig av med den mittersta av dessa bitar och lägg in den övre delen av en triangel med sidor som är lika långa som den bit som ska klippas bort. Vi har nu 4 linjesträckor som rör varandra i ändarna. Vi kan nu göra samma sak som med det första segmentet med var och en av de fyra bitarna. Vi kan nu göra samma sak om och om igen med alla de bitar vi får. Vi gör nu detta i all evighet och tittar på vad vi får i slutändan.

Längden på Koch-kurvan är oändlig och ytan på Koch-kurvan är noll. Detta är ganska märkligt. Ett linjesträck (med dimension 1) kan ha en längd på 1, men har en area på 0. En kvadrat med längd 1 och bredd 1 (med dimension 2) kommer att ha area 1 och längd oändligt.

Dimensionen likhet

Koch-kurvan verkar alltså vara större än något av dimension 1 och mindre än något av dimension 2. Tanken med likhetsdimensionen är att ge en dimension som ger en bättre uppfattning om längd eller yta för fraktaler. För en Koch-kurva vill vi alltså ha en dimension mellan 1 och 2.

Koch-kurvan kan delas upp i fyra delar som var och en är 1 3 {\displaystyle {\frac {1}{3}}} av originalets storlek. Vi kallar antalet bitar som en fraktal kan delas in i N {\displaystyle N} , och vi kallar storleksskillnaden B {\displaystyle B} . Vi sätter in dessa i ekvationen:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}}

Där log {\displaystyle \log } är logaritmen för ett tal. Detta tal är den Hausdorffska dimensionen för fraktalen. I Koch-kurvan är detta log 4 - log 13 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {\frac {1}{3}}}}=1.2619... } som vi ville.

Koch-kurvan är en av de enklaste fraktalformerna, och därför är dess dimensioner lätta att beräkna. Dess likhetsdimension och Hausdorff-dimension är båda lika stora. Detta gäller inte för mer komplexa fraktaler.

Koch snöflinga

Kochs snöflinga (eller Kochstjärna) är samma sak som Kochkurvan, förutom att den börjar med en liksidig triangel i stället för ett linjesegment.

Hur man gör Koch-kurvan

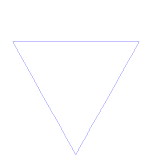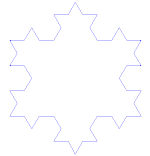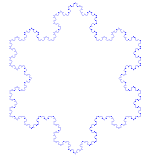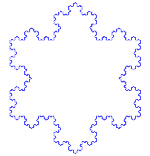
Använder

Fraktaler har många användningsområden, t.ex. inom biologin (lungor, njurar, hjärtfrekvensens variabilitet osv.), jordbävningar, inom finansbranschen där de är relaterade till de så kallade tunga svansfördelningarna och inom fysiken. Detta tyder på att fraktaler bör studeras för att förstå varför fraktaler är så vanliga i naturen.

Vissa fraktaler existerar endast av konstnärliga skäl, men andra är mycket användbara. Fraktaler är mycket effektiva former för radioantenner och används i datorchip för att effektivt koppla samman alla komponenter. Kustlinjer kan också betraktas som fraktaler.