Dimension | matematik och fysik

Mått är det sätt på vilket vi ser, mäter och upplever vår värld, genom att använda upp och ner, höger till vänster, bak till fram, varmt och kallt, hur tungt och hur långt, samt mer avancerade begrepp från matematik och fysik. Ett sätt att definiera en dimension är att titta på frihetsgrader, eller hur ett föremål kan röra sig i ett visst utrymme. Det finns olika begrepp eller sätt där begreppet dimension används, och det finns också olika definitioner. Det finns ingen definition som kan uppfylla alla begrepp.

I ett vektorrum V {\displaystyle V} $V$ (där vektorerna är "pilar" med riktningar) är dimensionen av V {\displaystyle V} $V$ , även skriven som dim ( V ) {\displaystyle \dim(V)} $\dim(V)$ , är lika med kardinaliteten (eller antalet vektorer) i en bas av V {\displaystyle V} $V$ (en uppsättning som anger hur många unika riktningar V {\displaystyle V} $V$ faktiskt har). Det är också lika med antalet av den största gruppen av rätlinjiga riktningar i det utrymmet. "Normala" föremål i vardagen specificeras av tre dimensioner, som brukar kallas längd, bredd och djup. Matematikerna kallar detta begrepp för euklidiskt rum.

Mått kan också användas för att mäta positioner. Avståndet till en position från en utgångspunkt kan mätas i längd-, bredd- och höjdriktningen. Dessa avstånd är ett mått på positionen.

I vissa fall används en fjärde (4D) dimension, tid, för att visa var en händelse befinner sig i tid och rum.

Ett diagram över de fyra första rumsliga dimensionerna.

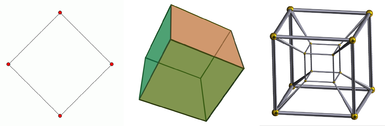
Från vänster till höger: kvadraten, kuben och tesserakt. Kvadraten är ett tvådimensionellt objekt, kuben är ett tredimensionellt objekt och tesserakt är ett fyrdimensionellt objekt. Ett 1-dimensionellt objekt är bara en linje. En projektion av kuben ges eftersom den ses på en tvådimensionell skärm. Detsamma gäller för tesserakt, som dessutom endast kan visas som en projektion även i ett tredimensionellt rum.

Andra dimensioner

Inom den moderna vetenskapen använder man andra dimensioner. Dimensioner som temperatur och vikt kan användas för att visa var något befinner sig i mindre enkla utrymmen. Forskare studerar dessa dimensioner med hjälp av dimensionsanalys.

Matematiker använder också dimensioner. Inom matematiken är dimensioner mer allmänna. Dimensioner i matematiken kanske inte mäter saker i världen. Reglerna för att räkna med dimensioner i matematik kan vara annorlunda än vanliga aritmetiska regler.

Mått och vektorer

Vektorer används för att visa avstånd och riktningar. Vektorer används ofta inom teknik och naturvetenskap och ibland inom matematiken.

En vektor är en lista med siffror. Det finns ett nummer för varje dimension. Det finns aritmetiska regler för vektorer.

Om Jane till exempel vill veta var Sally befinner sig kan Sally ge Jane en vektor som visar positionen. Om Jane och Sally befinner sig i världen finns det tre dimensioner. Därför ger Sally Jane en lista med tre tal för att visa hennes position. De tre siffrorna i vektorn som Sally ger Jane kan vara:

Sallys avstånd norr om Jane
Sallys avstånd öster om Jane
Sallys höjd över Jane

Relaterade sidor

3D
Hyperkuben, generalisering av kvadrat och kub bortom tre dimensioner
Minkowskis rymdtid, en fyrdimensionell manifest
Rymdtid

Frågor och svar

Fråga: Vad är en dimension?

A: En dimension är ett sätt att mäta, se och uppleva världen genom att använda begrepp som upp och ner, höger till vänster, bakåt till framåt, varmt och kallt, hur tungt och hur långt. Det kan också definieras som frihetsgrader eller det sätt på vilket ett föremål kan röra sig i ett visst utrymme.

F: Hur definierar matematiker det euklidiska rummet?

S: Matematiker definierar euklidiskt rum som specificerat av tre dimensioner som vanligtvis kallas längd, bredd och djup.

F: Vad är antalet vektorer i ett vektorrum?

S: Antalet vektorer i ett vektorrum är lika med kardinaliteten (eller antalet vektorer) i dess basuppsättning.

F: Hur många dimensioner används för att mäta position?

S: Tre dimensioner (längd, bredd och höjd) används för att mäta position. I vissa fall kan en fjärde (4D) dimension - tid - användas för att visa en händelses position i tid och rum.

F: Vad betyder dim(V)?

S: Dim(V) avser dimensionen för V som är lika med kardinaliteten (eller antalet vektorer) i dess basuppsättning eller lika med antalet riktningar i raka linjer som den har.

F: Finns det en definition som uppfyller alla begrepp som rör dimensioner?

S: Nej, det finns ingen enskild definition som kan uppfylla alla begrepp i samband med dimensioner.