Fyrfärgssatsen: definition, historia och datorbeviset för fyra färger
Upptäck fyrfärgssatsen: dess definition, fascinerande historia och det banbrytande datorbeviset som löste det klassiska kartfärgningsproblemet.
Fyrfärgssatsen är en klassisk matematisk sats som säger att varje karta på en plan yta kan färgläggas med högst fyra färger så att inga två regioner som är angränsande (dvs. delar ett helt gränssegment, inte bara en punkt) får samma färg. Tanken är densamma som när man färglägger politiska eller administrativa kartor: två områden som möts längs en gräns ska ha olika färg. Denna formulering kan också ges i grafteoretiska termer: fyrfärgssatsen är ekvivalent med påståendet att varje plan graf är 4-färgbar (att dess hörn kan färgas med fyra färger så att intilliggande hörn får olika färg).
Grundläggande egenskaper och exempel
Många enkla kartor kräver bara två eller tre färger. Den fjärde färgen behövs för särskilda konstruktioner, till exempel när ett område är omgivet av ett udda antal andra områden som rör vid varandra i en cykel; då uppstår ett arrangemang där tre färger inte räcker och en fjärde blir nödvändig. Teoremet om fem färger visar att fem färger alltid räcker för att färglägga en karta — detta teorem har ett kort och elementärt bevis och bevisades i slutet av 1800-talet (Heawood 1890). Att gå från fem till fyra färger visade sig dock vara mycket svårare. Ett sådant exempel på en karta som kräver fyra färger ges i bilden.
Historik i korthet
Problemet formulerades första gången 1852 av Francis Guthrie i samband med att han undersökte färgsättning av kartor över engelska grevskap. Under de följande decennierna publicerades många försök till bevis, varav flera senare visade sig vara felaktiga. Ett känt falskt bevis gavs 1879 av Alfred Kempe; hans idéer (särskilt begreppet Kempe-kedjor) var ändå viktiga och ledde så småningom till att femfärgssatsen bevisades.
Beviset med datorstöd och metodiken
Fyrfärgssatsen blev berömd bland annat därför att det var den första viktiga satsen som bevisades med ett stort inslag av datorarbete. Huvudidéerna i dessa datorbevis bygger på två centrala begrepp:
- Oundvikliga mängder: man visar att varje möjlig plan karta måste innehålla åtminstone ett inslag ur en viss ändlig mängd konfigurationer.
- Reducerbara konfigurationer: varje konfiguration i denna mängd visar sig vara sådan att om den förekommer i en minsta kontrarexempel-karta så kan man på ett standardiserat sätt bygga en färgning av hela kartan från en färgning av en mindre karta — vilket utesluter att ett kontrarexempel finns.
Metoden för att kombinera dessa idéer kallas ofta för discharging (urladdningsmetoden) tillsammans med kontroll av reducerbarhet för många fall. Ett tidigt försök att angripa problemet med denna metod gjordes av Herbert Heesch på 1960-talet.
Appel–Haken och efterföljande arbete
År 1976 presenterade Kenneth Appel och Wolfgang Haken ett bevis som använde datorer för att kontrollera ett stort antal fall: deras arbete visade att varje plan karta innehåller minst en av 1 936 reducerbara konfigurationer, och datorn användes för att verifiera reducerbarheten i dessa fall. Eftersom majoriteten av kontrollerna utfördes av datorprogram skapade detta initialt kontrovers och debatt om vad som utgör ett matematiskt bevis. Sedan dess har beviset förenklats och omarbetats flera gånger; ett senare känt fullständigare bevis av Robertson, Sanders, Seymour och Thomas (slutet av 1990-talet) minskade antalet nödvändiga fall till något över 600. Trots kritik har resultaten sedan dess bekräftats av flera oberoende implementationer och granskningar, och fyrfärgssatsen anses numera bevisad inom den matematiska gemenskapen.
Metoder som förekommer i bevisen
Flera tekniker spelar roll i bevismetoderna:
- Kempe-kedjor — en idé från det felaktiga 1879-beviset som dock ger användbara konstruktioner för att byta färger längs kedjor av hörn.
- Discharging (urladdning) — en bokföringsmetod för att visa att vissa lokala strukturer måste förekomma i varje plan graf.
- Datorkontroller — algoritmer som analyserar och verifierar många lokala konfigurationer (reducerbarhetskontroller).
Betydelse och tillämpningar
Trots sitt ursprung i kartfärgning är fyrfärgssatsen mer betydelsefull inom teoretisk matematik, särskilt grafteori och topologiska frågor. Kartografer ser sällan praktiska behov av just fyrfärgsegenskapen—enligt matematikhistorikern Kenneth May (Wilson 2002, 2) är det ovanligt att kartor endast använder fyra färger, och många kartor kräver färre än fyra färger—men satsen har varit central för utvecklingen av metoder inom diskret matematik och för hur datorer används i bevisföring. Dessutom leder satsen till algoritmer för att faktiskt konstruera en färgläggning av en plan graf; sådana algoritmer finns och kan implementeras effektivt.
Vanliga missförstånd
- Fyrfärgssatsen gäller bara när angränsning definieras som delning av ett helt gränssegment — om man tillåter kontakt i bara en punkt är påståendet felaktigt i den formen.
- Att satsen är ”bevisad med dator” innebär inte nödvändigtvis att beviset är ovetenskapligt; moderna verifieringar och oberoende implementationer har stärkt förtroendet för resultatet.
Sammantaget är fyrfärgssatsen ett intressant och historiskt viktigt exempel på hur matematiska idéer, nya metoder (som discharging) och datorhjälp kan kombineras för att lösa ett till synes enkelt men djupt problem.

Tre färger räcker inte för att färglägga den här kartan.

Exempel på en fyrfärgskarta
Exakt formulering av problemet
Intuitivt kan fyrfärgssatsen sägas vara: "Med tanke på att ett plan delas upp i sammanhängande områden, en så kallad karta, kan områdena färgas med högst fyra färger så att inga två angränsande områden har samma färg". För att kunna lösa problemet på ett korrekt sätt är det nödvändigt att klargöra vissa aspekter: För det första måste man bortse från alla punkter som tillhör tre eller fler länder. För det andra kan bisarra kartor med regioner med ändlig yta och oändlig omkrets kräva mer än fyra färger.
För att teoremet ska kunna tillämpas måste varje "land" vara ett enkelt sammanhängande område eller en sammanhängande region. I den verkliga världen är detta inte sant: Alaska som en del av Förenta staterna, Nakhchivan som en del av Azerbajdzjan och Kaliningrad som en del av Ryssland är inte sammanhängande. Eftersom territoriet i ett visst land måste ha samma färg kan det hända att fyra färger inte räcker. Tänk till exempel på en förenklad karta, som den som visas till vänster: På den här kartan tillhör de två regionerna med beteckningen A samma land och måste ha samma färg. Denna karta kräver då fem färger, eftersom de två A-regionerna tillsammans är sammanhängande med fyra andra regioner, som var och en är sammanhängande med alla de andra regionerna. Om A bara hade tre regioner skulle sex eller fler färger kunna behövas. På detta sätt är det möjligt att göra kartor som kräver ett godtyckligt stort antal färger. En liknande konstruktion gäller också om en enda färg används för alla vattenmassor, vilket är vanligt på verkliga kartor.
En enklare version av teoremet är baserad på grafteori. Mängden regioner i en karta kan representeras mer abstrakt som en oriktad graf som har en topp för varje region och en kant för varje par regioner som delar ett gränssegment. Grafen är plan: den kan ritas i planet utan korsningar genom att placera varje topp på en godtyckligt vald plats inom den region som den motsvarar, och genom att rita kanterna som kurvor som leder utan korsningar inom varje region från toppens plats till varje gemensam gränspunkt i regionen. Omvänt kan alla plana grafer bildas från en karta på detta sätt. I grafteoretisk terminologi säger fyrfärgssatsen att hörnpunkterna i varje planär graf kan färgas med högst fyra färger så att inga två angränsande hörnpunkter har samma färg, eller kort sagt att "varje planär graf är fyrfärgbar" (Thomas 1998, s. 849; Wilson 2002).

Exempel på en karta över Azerbajdzjan med icke sammanhängande regioner

Den här kartan kan inte färgas med fyra färger
Historia
Den första som gav problemet ett namn var Francis Guthrie år 1852. Han studerade då juridik i England. Han upptäckte att han behövde minst fyra färger för att färglägga en karta över Englands län. Augustus de Morgan diskuterade först problemet i ett brev till Rowan Hamliton i augusti 1852. I brevet frågar de Morgan om fyra färger verkligen räcker för att färglägga en karta så att länder som ligger bredvid varandra får olika färger.
Den engelske matematikern Arthur Cayley presenterade problemet för det matematiska samfundet i London 1878. Inom ett år hittade Alfred Kempe något som såg ut som ett bevis på problemet. Elva år senare, 1890, visade Percy Heawood att Alfreds bevis var fel. Peter Guthrie Tait presenterade ett nytt försök till bevis 1880. Det tog elva år att visa att Tait's bevis inte heller fungerade. År 1891 kunde Julius Petersen visa detta. När han falsifierade Cayleys bevis visade Kempe också ett bevis för ett problem som han kallade Five color theorem. Satsen säger att varje sådan karta kan färgas med högst fem färger. Det finns två begränsningar: För det första måste alla länder vara sammanhängande, det finns inga exklaver. Den andra begränsningen är att länderna måste ha en gemensam gräns; om de bara berörs i en punkt kan de färgas med samma färg. Även om Kempes bevis var felaktigt använde han några av de idéer som senare skulle möjliggöra ett korrekt bevis.
På 1960- och 1970-talen utvecklade Heinrich Heesch en första skiss till ett datoriserat bevis. Kenneth Appel och Wolfgang Haken förbättrade denna skiss 1976 (Robertson et al. 1996). De kunde minska antalet fall som skulle behöva testas till 1936; en senare version gjordes som förlitade sig på att endast testa 1476 fall. Varje fall behövde testas av en dator (Appel & Haken 1977) harv error: multiple targets (2×): CITEREFAppelHaken1977 (help).
År 1996 förbättrade Neil Robertson, Daniel Sanders, Paul Seymour och Robin Thomas metoden och minskade antalet fall som skulle testas till 663. Återigen måste varje fall testas med hjälp av en dator.
År 2005 utvecklade Georges Gonthier och Benjamin Werner ett formellt bevis. Detta var en förbättring, eftersom det för första gången gjorde det möjligt att använda programvara för teoremprövning. Den programvara som används kallas Coq.
Fyrfärgssatsen är det första stora matematiska problem som bevisades med hjälp av en dator. Eftersom beviset inte kan utföras av en människa erkände vissa matematiker det inte som korrekt. För att verifiera beviset är det nödvändigt att förlita sig på en korrekt fungerande programvara och hårdvara för att validera beviset. Eftersom beviset gjordes av en dator är det inte heller särskilt elegant.
Försök som visade sig vara felaktiga
Fyrfärgssatsen har varit ökänd för att ha dragit till sig ett stort antal falska bevis och motbevis under sin långa historia. Till en början vägrade New York Times att rapportera om Appel-Hakens bevis. Tidningen gjorde detta av politiska skäl; den fruktade att beviset skulle visa sig vara falskt i likhet med de tidigare bevisen (Wilson 2002, s. 209). Vissa bevis tog lång tid, tills de kunde falsifieras: Det tog över ett decennium att falsifiera Kempes och Taits bevis.
De enklaste motexemplen försöker i allmänhet skapa en region som berör alla andra. Detta tvingar de återstående regionerna att färgas med endast tre färger. Eftersom fyrfärgssatsen är sann är detta alltid möjligt, men eftersom den person som ritar kartan är fokuserad på den ena stora regionen märker han inte att de återstående regionerna faktiskt kan färgas med tre färger.
Detta trick kan generaliseras: Om färgerna för vissa områden på en karta väljs i förväg blir det omöjligt att färglägga de återstående områdena på ett sådant sätt att totalt sett endast fyra färger används. Någon som verifierar motexemplet kanske inte tänker på att det kan vara nödvändigt att ändra färgen på dessa regioner. Detta kommer att få motexemplet att se giltigt ut, även om det inte är det.
Kanske är en effekt som ligger bakom denna vanliga missuppfattning det faktum att färgbegränsningen inte är transitiv: en region behöver bara ha en annan färg än de regioner som den rör direkt, inte regioner som rör regioner som den rör. Om detta var begränsningen skulle plana grafer kräva ett godtyckligt stort antal färger.
Andra falska bevis bryter mot teoremets antaganden på oväntade sätt, t.ex. genom att använda en region som har flera separata delar eller genom att inte tillåta att regioner av samma färg rör sig vid en punkt.
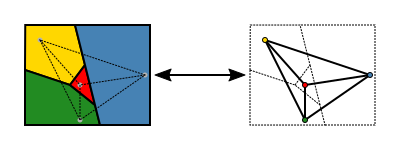
Kartan (vänster) har färgats med fem färger, och det är nödvändigt att ändra minst fyra av de tio regionerna för att få en färgning med endast fyra färger (höger).
Färgläggning av politiska kartor
I verkligheten har många länder exklaver eller kolonier. Eftersom de tillhör landet måste de färgas med samma färg som moderlandet. Detta innebär att det vanligtvis behövs mer än fyra färger för att färglägga en sådan karta. När matematiker talar om den graf som hör ihop med problemet säger de att den inte är plan. Även om det är lätt att kontrollera om en graf är planär är det mycket svårt att hitta det minsta antal färger som behövs för att färglägga den. Det är NP-komplett, vilket är ett av de svåraste problem som finns. Det minsta antalet färger som behövs för att färglägga en graf kallas dess kromatiska tal. Många av de problem som uppstår när man försöker lösa fyrfärgssatsen är relaterade till diskret matematik. Därför används ofta metoder från algebraisk topologi.
Utvidgning till "icke plana" kartor
Enligt fyrfärgssatsen måste "kartan" vara på en plan yta, det som matematiker kallar ett plan. År 1890 skapade Percy John Heawood det som idag kallas Heawoods gissning: Den ställer samma fråga som fyrfärgssatsen, men för vilket topologiskt objekt som helst. Som exempel kan en torus färgas med högst sju färger. Heawoods gissning ger en formel som fungerar för alla sådana objekt, utom Klein-flaskan.
Frågor och svar
F: Vad är fyrfärgssatsen?
S: Fyrfärgssatsen är en matematisk sats som säger att i varje plan yta med regioner kan regionerna färgas med högst fyra färger. Angränsande regioner får inte få samma färg.
F: Hur fastställdes det första beviset för fyrfärgssatsen?
S: Det första beviset för fyrfärgssatsen var ett bevis genom utmattning med 1 936 fall. Detta innebär att det fastställdes genom att det delades upp i fall och att varje fall bevisades separat.
F: Är kartmakare intresserade av detta problem?
Svar: Nej, kartmakare är inte särskilt intresserade av detta problem eftersom kartor som endast använder fyra färger är sällsynta och vanligtvis kräver endast tre färger. Böcker om kartografi och kartframställningens historia nämner inte fyrfärgsegenskapen.
F: Vad är femfärgssatsen?
S: Enligt femfärgssatsen räcker det med fem färger för att färglägga en karta och den har ett kort, elementärt bevis som bevisades i slutet av 1800-talet.
F: Hur svårt var det att bevisa att det endast behövs fyra färger för att färglägga kartor?
Svar: Att bevisa att det endast behövs fyra färger för att färglägga kartor visade sig vara mycket svårare än väntat, eftersom många falska bevis och falska motbevis har dykt upp sedan det första påståendet 1852.
F: Finns det något exempel på en karta där det skulle behövas 5 eller fler färger för att färga alla regioner korrekt?
S: Ja, ett sådant exempel är när en region är omgiven av ett udda antal andra regioner som berör varandra i en cykel - 5 eller fler färger kan vara nödvändiga för att färga alla regioner korrekt i detta fall.
Sök

