Heavisidefunktion
Heavisidefunktionen H är en icke-kontinuerlig funktion vars värde är noll för en negativ inmatning och ett för en positiv inmatning.
Funktionen används inom matematiken i styrteori för att representera en signal som aktiveras vid en bestämd tidpunkt och förblir aktiverad på obestämd tid. Den har fått sitt namn efter engelsmannen Oliver Heaviside.
Heaviside-funktionen är integralen av Dirac-deltafunktionen: H′ = δ. Detta skrivs ibland som
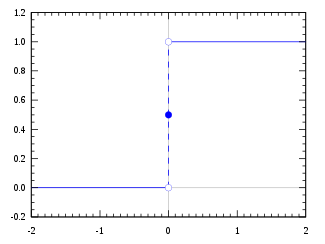
Heavisides stegfunktion, med användning av halvmaximumskonventionen
Diskret form
Vi kan också definiera en alternativ form av Heavisides stegfunktion som en funktion av en diskret variabel n:
H [ n ] = { 0 , n < 0 1 , n ≥ 0 {\displaystyle H[n]={\begin{cases}0,&n<0\\\1,&n\geq 0\end{cases}}}
där n är ett heltal.
Eller
H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)}
Den diskreta tidsenhetsimpulsen är den första differensen av det diskreta tidssteget.
δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1]. }
Denna funktion är den kumulativa summeringen av Kroneckerdeltat:
H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}
där
δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0}\,}
är den diskreta enhetsimpulsfunktionen.
Representationer
Ofta är en integralrepresentation av Heavisides stegfunktion användbar:
H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e i x τ d τ . {\displaystyle H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau . } 
H(0)
Funktionens värde vid 0 kan definieras som H(0) = 0, H(0) = ½ eller H(0) = 1.
H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} 
Relaterade sidor
- Laplace-transformation
Frågor och svar
F: Vad är Heaviside-funktionen?
S: Heaviside-funktionen är en icke-kontinuerlig funktion vars värde är noll för en negativ ingång och ett för en positiv ingång.
F: Varför används Heaviside-funktionen i reglerteori?
S: Heaviside-funktionen används i reglerteori för att representera en signal som slås på vid en viss tidpunkt och förblir påslagen i det oändliga.
F: Vem är personen efter vilken Heaviside-funktionen fick sitt namn?
S: Heaviside-funktionen har fått sitt namn efter engelsmannen Oliver Heaviside.
F: Vad är förhållandet mellan Heaviside-funktionen och Dirac delta-funktionen?
S: Heavisidefunktionen är integralen av Dirac deltafunktionen: H′(x)= δ(x).
F: Vad ger Heavisidefunktionen för positiva indata?
S: Heaviside-funktionen ger ett värde för positiva indata.
F: Vad ger Heaviside-funktionen för negativa ingångsvärden?
S: Heaviside-funktionen ger noll för negativa indata.
F: Vilken typ av funktion är Heaviside-funktionen?
S: Heaviside-funktionen är en icke-kontinuerlig funktion.
Sök
![{\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}](https://www.alegsaonline.com/image/efb65c686bdec46712eae1997c363f7ef8709b79.svg)

![{\displaystyle \delta \left[n\right]=H[n]-H[n-1].}](https://www.alegsaonline.com/image/e6c417f161a7987a4db18818743eeb23494b0feb.svg)
![{\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}](https://www.alegsaonline.com/image/5db28db3163e2940aaf93d0fc180edb19d865d32.svg)
![{\displaystyle \delta [k]=\delta _{k,0}\,}](https://www.alegsaonline.com/image/97a99ab7d257c74f38fbb2d42c8e42e1cb16d0e9.svg)