Ljusklocka – definition och tidsutvidgning i speciell relativitet
Klar och intuitiv förklaring av ljusklockan och tidsutvidgning i speciell relativitet, med algebraiska exempel och Pythagoras för att räkna hur tiden saktas ner.
Ljusklockan och idén bakom
Ljusklockan är ett enkelt och tydligt sätt att illustrera en grundläggande egenskap i speciella relativitetsteorin. Konstruktionen består i korthet av en ljuskälla ( längst ner på en stång ), en spegel (överst) och en detektor vid basen som registrerar när den reflekterade ljusblixten återvänder. Varje gång detektorn ser en blink räknas en "tick" och en ny blink skickas upp till spegeln. Eftersom ljusets hastighet är konstant kan vi exakt beräkna hur lång tid en tick tar i olika rörelseförhållanden och därigenom visa fenomenet tidsutvidgning.
En liknelse för att förstå relativ rörelse
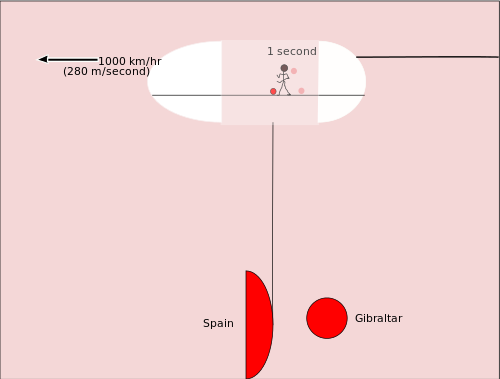
Tänk dig en spelare som dribblar en basketboll i lastrummet på ett flygplan. För spelaren (i flygplanet) går dribblingarna ungefär som vanligt, men för en observatör på marken ser varje studs röra sig framåt i planetets riktning — bollen färdas en längre sträcka relativt marken än vad den gör relativt spelaren. Detta visar på skillnaden mellan rörelsen i klockans egen referensram och i en annan referensram som ser klockan i rörelse.
Ljusklockan vid Nordpolen (klockans viloram)
Anta att vi bygger en ljusklocka vid ett teleskop på Nordpolen. Avståndet mellan ljuskällan i botten och spegeln i toppen är a. När klockan står stilla i vår referensram (Nordpolen) färdas ljuset en sträcka 2a (upp + ner) vid hastigheten c. Tiden mellan två tick är därför
t = 2a / c.
I textexemplet kan vi ta a = 0,5 km, vilket ger att ljuset färdas 1 km per tick och därmed t = 1 km / 300 000 km/s ≈ 3,333·10-6 s.
Observerad klocka när den rör sig (jordobservation)
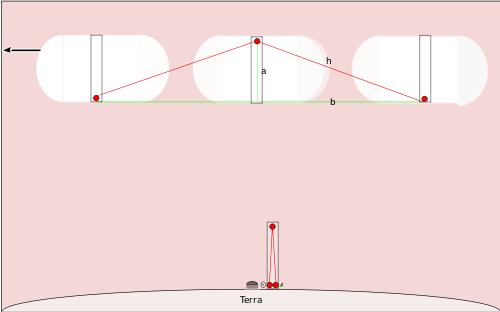
Tänk nu att ett rymdskepp med en likadan ljusklocka passerar över Nordpolen med hastighet r (i praktiken en stor del av ljusets hastighet). För en observatör på marken är situationen annorlunda: medan ljusblixten färdas upp mot spegeln rör sig basen av klockan framåt, så ljusets bana i observatörens referensram blir sned (en hypotenusa). På samma sätt blir vägen ner en annan sned bana. Varje halvresa (upp eller ner) i observatörens ram bildar en rätvinklig triangel med höjden a och basen (r t'/2), där t' är den tid observatören på jorden mäter mellan start och återkomst av en blink (alltså tiden för en tick enligt jordens observatörer).
Härledning med Pythagoras
För halva färdsträckan (upp eller ner) blir hypotenusan
h = √(a2 + (r t'/2)2).
Totala sträckan ljuset färdas enligt jordobservatören är då d = 2h. Eftersom ljuset färdas med hastighet c gäller också
c t' = 2 √(a2 + (r t'/2)2).
Vi löser denna ekvation för t' enligt följande enkla steg:
- Dela båda sidor med 2: (c t')/2 = √(a2 + (r t'/2)2)
- Kvadrera båda sidor: (c2 t'2)/4 = a2 + (r2 t'2)/4
- Samlade t'2-termer: (c2 t'2)/4 − (r2 t'2)/4 = a2
- Faktorera: (t'2/4) (c2 − r2) = a2
- Lös för t': t'2 = 4 a2 / (c2 − r2) = (4 a2/c2) · 1/(1 − r2/c2)
- Ta kvadratroten och använd t = 2a/c (klockans tick i viloramen):
t' = (2a / c) · 1 / √(1 − r2/c2) = t / √(1 − r2/c2).
Tolkning: tidsutvidgning och gamma-faktorn
Uttrycket ovan visar den välkända tidsutvidgningen i speciell relativitet. Tiden mellan ticks i klockans egen vila (kallad proper tid och här betecknad t) är kortare än den tid en observatör ser för samma tick när klockan rör sig. Faktor som förlänger tiden kallas Lorentzfaktorn eller gamma:
γ = 1 / √(1 − r2/c2), så t' = γ t.
Alltså: ju snabbare rymdskeppet rör sig (ju närmare c), desto större blir γ och desto mer utdragen blir tiden mätt av jordobservatören. Detta innebär att en rörlig klocka "tickar långsammare" jämfört med samma klocka i vila (ur perspektivet hos observatören som ser klockan i rörelse).
Exempel
Om t = 1 s och r = 0,5 c får vi γ = 1 / √(1 − 0,25) = 1 / √0,75 ≈ 1,1547. Då blir t' ≈ 1,1547 s — alltså cirka 15,5 % längre tid för varje tick enligt observatörer som ser rymdskeppet röra sig.
I vårt tidigare numeriska exempel med a = 0,5 km gavs t ≈ 3,333·10−6 s; vid samma hastighet r = 0,5 c blir t' ≈ 3,849·10−6 s.
Ytterligare kommentarer och experiment
Det är viktigt att notera att tidsutvidgningen är relativ: observatörer i rymdskeppet ser istället jordens klockor som förlängda på samma sätt (symmetri), och full förståelse kräver också begreppet samtidighet i olika referensramar. Effekten har bekräftats i många experiment — till exempel genom att jämföra atomklockor i höghastighetsflygningar eller partiklars ökade livslängd vid höga hastigheter.
Du kan experimentera numeriskt med olika hastigheter här: http://www.1728.org/reltivty.htm
Frågor och svar
F: Vad är en ljusklocka?
S: En ljusklocka är en anordning som är utformad för att visa en grundläggande egenskap hos den speciella relativitetsteorin. Den fungerar genom att reflektera en ljusblixt från en avlägsen spegel och använda dess återkomst för att utlösa en annan ljusblixt, samtidigt som den räknar hur många ljusblixtar som har uppstått på vägen.
F: Vad är tidsutvidgning?
Svar: Tidsutvidgning är ett fenomen som uppstår när människor på jorden ser ett rymdskepp flyga med hjälp av en ljusklocka. De ser att den tickar relativt långsamt under inflytande av relativiteten.
F: Hur kan vi beräkna hur mycket tiden saktar ner i ett rymdskepp?
Svar: Vi kan använda algebra och Pythagoras sats för att beräkna hur mycket tiden saktar ner i ett rymdskepp. Vi måste tillämpa ekvationen d = rt (avstånd är lika med hastighet gånger tid) och använda ljusets konstanta hastighet c i två problem.
F: Hur fungerar en ljusklocka?
S: En ljusklocka består av en ljuskälla längst ner på en lång stav med en spegel högst upp och en elektronisk detektor längst ner. När den slås på passerar en enda ljusblixt från botten till toppen, där den reflekteras nedåt och upptäcks av detektorn i botten, som lägger till en räknare till den bifogade räknaren och utlöser en ny ljusblixt uppåt igen. Processen fortsätter tills den stoppas eller återställs.
F: Vilken ekvation behöver vi för denna beräkning?
Svar: Vi behöver t' = 2a/(c√(1-r2/c2)), där t' (tiden mellan klockan på Nordpolen) är lika med 2a/c dividerat med √(1-r2/c2). Om t = 1 sekund, och om den färdas med halva ljusets hastighet, är t' = 1,1547 sekunder.
F. Hur förhåller sig Pythagoras sats till denna beräkning?
Svar: Pythagoras sats hjälper oss att hitta h (hypotenusan), som är en del av ekvationen som gör att vi kan beräkna hur länge varje tick varar i sekunder (d=ct). När vi känner till h kan vi lösa t', som talar om hur länge varje stygn varar enligt människorna på jorden som tittar från Nordpolen och människorna på själva fartyget, som passerar över dem mycket snabbt.
Sök