Algebra | en del av matematiken

Algebra (från arabiska: الجبر, translittererat "al-jabr", som betyder "återförening av trasiga delar") är en del av matematiken. Den använder variabler för att representera ett värde som ännu inte är känt. När ett likhetstecken (=) används kallas detta för en ekvation. En mycket enkel ekvation som använder en variabel är: 2 + 3 = x {\displaystyle 2+3=x} $2+3=x$ . I det här exemplet är x = 5 {\displaystyle x=5} $x=5$ Det kan också sägas att "x {\displaystyle x} är lika med fem". Detta kallas att lösa x {\displaystyle x} .

Förutom ekvationer finns det ojämlikheter (mindre än och större än). En speciell typ av ekvation kallas funktion. Denna används ofta när man gör grafer eftersom den alltid omvandlar en ingång till en utgång.

Algebra kan användas för att lösa verkliga problem eftersom algebrareglerna fungerar i verkligheten och siffror kan användas för att representera värden för verkliga saker. Fysik, teknik och dataprogrammering är områden där algebra används hela tiden. Det är också användbart att känna till inom lantmäteri, konstruktion och affärsverksamhet, särskilt redovisning.

Personer som använder sig av algebra använder sig av talregler och matematiska operationer som används på tal. De enklaste är att addera, subtrahera, multiplicera och dividera. Mer avancerade operationer involverar exponenter och börjar med kvadrater och kvadratrötter.

Algebra användes först för att lösa ekvationer och olikheter. Två exempel är linjära ekvationer (ekvationen för en rak linje, y = m x + b {\displaystyle y=mx+b} $y=mx+b$ eller y = m x + c {\displaystyle y=mx+c} $y=mx+c$ ) och kvadratiska ekvationer, där variablerna är kvadrerade (multiplicerade med sig själva, t.ex: 2 ⋅ 2 {\displaystyle 2\cdot 2} $2\cdot 2$ , 3 ⋅ 3 {\displaystyle 3\cdot 3} $3\cdot 3$ , eller x ⋅ x {\displaystyle x\cdot x} $x\cdot x$ ).

Historia

Tidiga former av algebra utvecklades av babylonierna och grekiska geometriker som Hero av Alexandria. Ordet "algebra" är dock en latinsk form av det arabiska ordet Al-Jabr ("gjutning") och kommer från en matematikbok Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Uppsats om beräkningen av gjutning och ekvation") som skrevs på 800-talet av en persisk matematiker, Muhammad ibn Mūsā al-Khwārizmī, som var muslim och född i Khwarizm i Uzbekistan. Han blomstrade under Al-Ma'moun i Bagdad i Irak under åren 813-833 e.Kr. och dog omkring 840 e.Kr. Boken fördes till Europa och översattes till latin på 1100-talet. Boken fick då namnet "algebra". (Slutet på matematikerns namn, al-Khwarizmi, ändrades till ett ord som var lättare att säga på latin och blev det engelska ordet algorithm).

Exempel

Här är ett enkelt exempel på ett algebraproblem:

Sue har 12 godis och Ann har 24 godis. De bestämmer sig för att dela med sig så att de får lika många godis. Hur många godis kommer var och en av dem att ha?

Här är de steg som du kan använda för att lösa problemet:

För att få samma antal godis måste Ann ge några till Sue. Låt x {\displaystyle x} representera antalet godis som Ann ger till Sue.
Sues godis plus x {\displaystyle x} måste vara samma som Anns godis minus x {\displaystyle x} . Detta skrivs som: 12 + x = 24 - x {\displaystyle 12+x=24-x} $12+x=24-x$
Subtrahera 12 från båda sidor av ekvationen. Detta ger: x = 12 - x {\displaystyle x=12-x} $x=12-x$ . (Det som händer på ena sidan av likhetstecknet måste också hända på den andra sidan för att ekvationen fortfarande ska vara sann. Så i det här fallet, när 12 subtraherades från båda sidor, blev det ett mellansteg på 12 + x - 12 = 24 - x - 12 {\displaystyle 12+x-12=24-x-12} $12+x-12=24-x-12$ . När en person är bekväm med detta skrivs inte mellansteget ner).
Lägg till x {\displaystyle x} på båda sidor av ekvationen. Detta ger: 2 x = 12 {\displaystyle 2x=12} $2x=12$
Dela båda sidorna av ekvationen med 2. Detta ger x = 6 {\displaystyle x=6} $x=6$ . Svaret är sex. Detta innebär att om Ann ger Sue 6 godis, kommer de att ha samma antal godis.
För att kontrollera detta, sätt tillbaka 6 i den ursprungliga ekvationen där x {\displaystyle x} var: 12 + 6 = 24 - 6 {\displaystyle 12+6=24-6} $12+6=24-6$
Detta ger 18 = 18 {\displaystyle 18=18} $18=18$ vilket är sant. De har nu 18 godis vardera.

Med lite övning kan algebra användas när man står inför ett problem som är för svårt att lösa på något annat sätt. Problem som att bygga en motorväg, konstruera en mobiltelefon eller hitta ett botemedel mot en sjukdom kräver alla algebra.

Skrivalgebra

Som i de flesta delar av matematiken skrivs addition av y {\displaystyle y} och z {\displaystyle z} $z$ (eller y {\displaystyle y} plus z {\displaystyle z} $z$ ) som y + z {\displaystyle y+z} $y+z$ ;

subtraktion av z {\displaystyle z} $z$ från y {\displaystyle y} (eller y {\displaystyle y} minus z {\displaystyle z} $z$ ) skrivs som y - z {\displaystyle y-z} $y-z$ ;

och dividerar y {\displaystyle y} med z {\displaystyle z} $z$ (eller y {\displaystyle y} över z {\displaystyle z} $z$ ) skrivs som y / z {\displaystyle y/z} $y/z$ eller y z {\displaystyle y \over z} ${y \over z}$ .

I algebra kan multiplikation av y {\displaystyle y} med z {\displaystyle z} $z$ (eller y {\displaystyle y} gånger z {\displaystyle z} $z$ ) skrivas på tre olika sätt: y ⋅ z {\displaystyle y\cdot z} $y\cdot z$ , y ( z ) {\displaystyle y(z)} $y(z)$ eller bara y z {\displaystyle yz} $yz$ . Alla dessa beteckningar betyder samma sak: y {\displaystyle y} gånger z {\displaystyle z} $z$ . Symbolen " × {\displaystyle \times } $\times$ " som används i aritmetik används inte i algebra, eftersom den liknar bokstaven x {\displaystyle x} , som ofta används som en variabel.

När vi multiplicerar ett tal och en variabel i algebra kan vi helt enkelt skriva talet framför bokstaven: 5 ⋅ y ⟺ 5 y {\displaystyle 5\cdot y\iff 5y} $5\cdot y\iff 5y$ . När talet är 1 skrivs det inte eftersom 1 gånger vilket tal som helst är det talet ( 1 ⋅ y = y {\displaystyle 1\cdot y=y} $1\cdot y=y$ ) och därför behövs det inte. Och när det är 0 kan vi helt ta bort termerna, eftersom 0 gånger vilket tal som helst är noll ( 0 ⋅ y = 0 {\displaystyle 0\cdot y=0} $0\cdot y=0$ ).

Som en liten notis kan nämnas att du inte behöver använda bokstäverna x {\displaystyle x} eller y {\displaystyle y} i algebra. Variabler är bara symboler som betyder något okänt tal eller värde, så du kan använda vilken bokstav som helst för en variabel (utom e {\displaystyle e} $e$ (Eulers tal) och i {\displaystyle i} $i$ (imaginär enhet), eftersom dessa är matematiska konstanter). x {\displaystyle x} och y {\displaystyle y} är dock de vanligaste.

Funktioner och grafer

En viktig del av algebra är studiet av funktioner, eftersom de ofta förekommer i ekvationer som vi försöker lösa. En funktion är som en maskin som du kan sätta in ett tal (eller flera tal) i och få ut ett visst tal (eller flera tal). När man använder funktioner kan grafer vara kraftfulla verktyg som hjälper oss att studera ekvationernas lösningar.

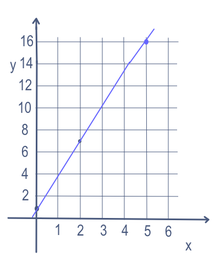
En graf är en bild som visar alla värden för de variabler som gör ekvationen eller ojämlikheten sann. Vanligtvis är detta lätt att göra när det bara finns en eller två variabler. Grafen är ofta en linje, och om linjen inte böjer sig eller går rakt upp och ner kan den beskrivas med grundformeln y = m x + b {\displaystyle y=mx+b} $y=mx+b$ . Variabeln b {\displaystyle b} $b$ är grafens y-intercept (där linjen korsar den vertikala axeln) och m {\displaystyle m} är linjens lutning eller branthet. Denna formel gäller för koordinaterna i en graf, där varje punkt på linjen skrivs ( x {\displaystyle x} , y {\displaystyle y} ).

I vissa matematiska problem, t.ex. ekvationen för en linje, kan det finnas mer än en variabel (i det här fallet x {\displaystyle x} och y {\displaystyle y} ). För att hitta punkter på linjen ändras en variabel. Den variabel som ändras kallas den "oberoende" variabeln. Sedan görs matematiken för att få fram ett tal. Det tal som skapas kallas den "beroende" variabeln. Oftast skrivs den oberoende variabeln som x {\displaystyle x} och den beroende variabeln som y {\displaystyle y}. till exempel i y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$ . Detta visas ofta i ett diagram med en x-axel {\displaystyle x} (som går åt vänster och höger) och en y-axel {\displaystyle y} (som går upp och ner). Det kan också skrivas i funktionsform: f ( x ) = 3 x + 1 {\displaystyle f(x)=3x+1} $f(x)=3x+1$ . Så i detta exempel kan vi sätta in 5 för x {\displaystyle x} och få y = 16 {\displaystyle y=16} $y=16$ . Genom att sätta in 2 för x {\displaystyle x} skulle vi få y = 7 {\displaystyle y=7} $y=7$ . Och 0 för x {\displaystyle x} skulle ge y = 1 {\displaystyle y=1} $y=1$ . Det skulle alltså finnas en linje som går genom punkterna (5,16), (2,7) och (0,1), vilket framgår av grafen till höger.

Om x {\displaystyle x} har en potens av 1 är det en rät linje. Om den är kvadrerad eller har en annan potens är den krökt. Om den använder en ojämlikhet ( < < {\displaystyle <} $<$ eller > {\displaystyle >} $>$ ), är vanligtvis en del av grafen skuggad, antingen över eller under linjen.

Linjär ekvation för y = 3 x + 1 {\displaystyle y=3x+1} $y=3x+1$

Regler

I algebra finns det några regler som kan användas för att förstå ekvationer bättre. Dessa kallas algebraregler. Även om dessa regler kan verka meningslösa eller uppenbara är det klokt att förstå att dessa egenskaper inte gäller inom alla grenar av matematiken. Därför är det bra att veta hur dessa axiomatiska regler förklaras, innan man tar dem för givna. Innan du går vidare till reglerna bör du reflektera över två definitioner som kommer att ges.

Motsats: motsatsen till en {\displaystyle a} är - en {\displaystyle -a} .
Reciprok: Reciproken av en {\displaystyle a} är 1 a {\displaystyle {\frac {1}{a}}} ${\frac {1}{a}}$ .

Kommutativ egenskap för addition

"Kommutativ" innebär att en funktion får samma resultat om man byter ut siffrorna. Med andra ord spelar ordningen på termerna i en ekvation ingen roll. När två termer (addender) adderas gäller den "kommutativa egenskapen för addition". I algebraiska termer ger detta a + b = b + a {\displaystyle a+b=b+a} a+b=b+a .

Observera att detta inte gäller för subtraktion (dvs. a - b ≠ b - a {\displaystyle a-b\neq b-a} $a-b\neq b-a$ utom om a = b {\displaystyle a=b} $a=b$ ).

Kommutativ egenskap för multiplikation

När två termer (faktorer) multipliceras gäller "multiplikationens kommutativa egenskap". I algebraiska termer ger detta a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} $a\cdot b=b\cdot a$ .

Observera att detta inte gäller för division (dvs. a b ≠ b a {\displaystyle {\frac {\frac {a}{b}}}\neq {\frac {b}{a}}}) ${\frac {a}{b}}\neq {\frac {b}{a}}$ när a ≠ 0 {\displaystyle a\neq 0} $a\neq 0$ och b ≠ 0 {\displaystyle b\neq 0} $b\neq 0$ , utom om a = b {\displaystyle a=b} $a=b$ ).

Associativ egenskap hos addition

"Associativ" avser gruppering av tal. Den associativa egenskapen hos addition innebär att när man adderar tre eller fler termer spelar det ingen roll hur dessa termer är grupperade. Algebraiskt ger detta a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Observera att detta inte gäller för subtraktion, t.ex. 1 - ( 2 - 3 ) ≠ ( 1 - 2 ) - 3 {\displaystyle 1-(2-3)\neq (1-2)-3} $1-(2-3)\neq (1-2)-3$ (se distributiv egenskap).

Associativ egenskap för multiplikation

Multiplikationens associativa egenskap innebär att när man multiplicerar tre eller fler termer spelar det ingen roll hur dessa termer är grupperade. Algebraiskt ger detta a ( b c ) = ( a b ) c {\displaystyle a(bc)=(ab)c} $a(bc)=(ab)c$ . Observera att detta inte gäller för division, t.ex. 1 / ( 2 / 4 ) ≠ ( 1 / 2 ) / 4 {\displaystyle 1/(2/4)\neq (1/2)/4} $1/(2/4)\neq (1/2)/4$ .

Distributiv egenskap

Den distributiva egenskapen säger att multiplikationen av en term med en annan term kan distribueras. Till exempel: a ( b + c ) = a b + a c {\displaystyle a(b+c)=ab+ac} $a(b+c)=ab+ac$ . (Förväxla inte detta med de associativa egenskaperna! Till exempel: a ( b + c ) ≠ ( a b ) + c {\displaystyle a(b+c)\neq (ab)+c} $a(b+c)\neq (ab)+c$ .)

Additiv identitet

Identitet är ett tals egenskap att det är lika med sig självt. Med andra ord finns det en operation av två tal som gör att det är lika med variabeln i summan. Den additiva identitetsegenskapen säger att varje tal plus 0 är det talet: a + 0 = a {\displaystyle a+0=a} a+0=a . Detta gäller även för subtraktion: a - 0 = a {\displaystyle a-0=a} a-0=a .

Multiplikativ identitet

Den multiplikativa identitetsegenskapen säger att varje tal gånger 1 är detta tal: a ⋅ 1 = a {\displaystyle a\cdot 1=a} $a\cdot 1=a$ . Detta gäller även för division: a 1 = a {\displaystyle {\frac {a}{1}}}=a} ${\frac {a}{1}}=a$ .

Additiv invers egenskap

Den additiva inversegenskapen är ungefär som motsatsen till den additiva identiteten. När vi adderar ett tal och dess motsats blir resultatet 0. Algebraiskt sett kan man säga följande: a + - a = 0 {\displaystyle a+-a=0} $a+-a=0$ , vilket är samma sak som a - a = 0 {\displaystyle a-a=0} $a-a=0$ . Till exempel är den additiva inversen (eller motsatsen) till 1 -1.

Multiplikativ invers egenskap

Den multiplikativa inversegenskapen innebär att när vi multiplicerar ett tal med dess inversa blir resultatet 1. Algebraiskt sett säger den följande: a ⋅ $a\cdot {\frac {1}{a}}=1$ , vilket är samma sak som a a = 1 {\displaystyle {\frac {a}{a}}=1} ${\frac {a}{a}}=1$ . Till exempel är den multiplikativa inversen (eller bara inversen) av 2 1/2. För att få inversen av ett bråk byter man om på täljaren och nämnaren: inversen av 2 3 {\displaystyle {\frac {2}{3}}}} ${\frac {2}{3}}$ är 3 2 {\displaystyle {\frac {3}{2}}}} ${\frac {3}{2}}$ .

Avancerad algebra

Förutom "elementär algebra", eller grundläggande algebra, finns det avancerade former av algebra som lärs ut på högskolor och universitet, t.ex. abstrakt algebra, linjär algebra och universell algebra. Detta inkluderar hur man använder en matris för att lösa många linjära ekvationer på en gång. Abstrakt algebra är studiet av saker som återfinns i ekvationer, som går bortom siffror till det mer abstrakta med grupper av siffror.

Många matematiska problem handlar om fysik och teknik. I många av dessa fysikproblem är tid en variabel. Den bokstav som används för tid är t {\displaystyle t} $t$ . Att använda de grundläggande idéerna i algebra kan hjälpa till att reducera ett matematiskt problem till dess enklaste form vilket gör det lättare att lösa svåra problem. Energi är e {\displaystyle e} $e$ , kraft är f {\displaystyle f} , massa är m {\displaystyle m} , acceleration är a {\displaystyle a} och ljusets hastighet är ibland c {\displaystyle c} $c$ . Detta används i några kända ekvationer, som f = m a {\displaystyle f=ma} $f=ma$ och e = m c 2 {\displaystyle e=mc^{2}}} $e=mc^{2}$ (även om det krävdes mer komplicerad matematik än algebra för att komma fram till den sista ekvationen).

Relaterade sidor

Förteckning över matematiska ämnen
Arbetsordning
Parabola
System för datoralgebra

Frågor och svar

F: Vad är algebra?

S: Algebra är en del av matematiken som använder variabler för att representera ett värde som ännu inte är känt.

F: Vad betyder ett likhetstecken i algebra?

S: Ett likhetstecken (=) betecknar en ekvation i algebra.

F: Vad är en funktion i algebra?

S: En funktion i algebra är en speciell typ av ekvation som alltid omvandlar en inmatning till en utmatning.

F: Hur kan algebra användas för att lösa verkliga problem?

S: Algebra kan användas för att lösa verkliga problem eftersom algebraens regler fungerar i det verkliga livet och siffror kan användas för att representera värden för verkliga saker. Fysik, teknik och dataprogrammering är områden där algebra används hela tiden. Det är också användbart att känna till inom lantmäteri, konstruktion och affärsverksamhet, särskilt redovisning.

F: Vilka är några matematiska operationer som används på tal i algebra?

S: I algebra använder man sig av talregler och matematiska operationer som att addera, subtrahera, multiplicera och dividera tal. Mer avancerade operationer involverar exponenter, med början i kvadrater och kvadratrötter.

F: Vad är exempel på ekvationer som används i algebra?

S: Exempel på ekvationer som används i algebra är linjära ekvationer (ekvationen för en rak linje) och kvadratiska ekvationer som har variabler som är kvadrerade (multiplicerade med sig själva).