Parallellpostulatet: Euklids femte postulat förklarat
Upptäck Euklids parallellpostulat: förklaring, historik och hur det skiljer euklidisk från icke‑euklidisk geometri.
Inom geometrin är parallellpostulatet ett av axiomen i euklidisk geometri. Ibland kallas det också för Euklids femte postulat, eftersom det är det femte postulatet i Euklids Elementar. Postulatet utgör en grundläggande antagelse om hur räta linjer och vinklar förhåller sig i planet och påverkar många geometriska satser.
Postulatet säger att:
Om du skär ett linjesträck med två linjer och de två inre vinklarna som linjerna bildar är mindre än 180°, kommer de två linjerna att mötas om du förlänger dem tillräckligt länge.
En vanlig modern och ekvivalent formulering är Playfairs axiom:
- Playfairs axiom: För en given linje och en punkt utanför den finns exakt en linje genom punkten som inte skär den givna linjen (alltså är parallell).
Varför är postulatet speciellt?
Till skillnad från de andra axiomen i Euklids verk kunde parallellpostulatet inte enkelt härledas från de övriga antagandena. Under nästan två tusen år försökte många matematiker bevisa det ur de andra postulatena utan att använda det uttryckligen. Misslyckanden med sådana försök ledde i början av 1800‑talet till upptäckten av icke‑euklidisk geometri.
Historia och utveckling
- Försök att bevisa parallellpostulatet ledde fram till arbete av bland andra Saccheri och Lambert på 1700‑talet, som formulerade olika strategier och undersökte konsekvenserna av att anta dess negation.
- På 1800‑talet utvecklade Nikolaj Lobachevskij och János Bolyai oberoende av varandra en konsekvent hyperbolisk geometri där parallellpostulatet ersätts av en annan regel — i sådan geometri finns fler än en linje genom en punkt som inte skär en given linje.
- Carl Friedrich Gauss hade också kommit fram till liknande idéer men publicerade dem inte. Senare gav Eugenio Beltrami, Felix Klein och Henri Poincaré modeller som visade att hyperbolisk geometri var lika konsistent som euklidisk geometri, under förutsättning att den euklidiska är konsekvent.
Konsekvenser och ekvivalenta påståenden
Parallellpostulatet är ekvivalent med flera andra påståenden i plan geometri. Några viktiga exempel är:
- Summan av vinklarna i en triangel är 180°.
- Det finns rektanglar (en fyrhörning med fyra räta vinklar).
- Genom en punkt utanför en linje går högst en linje som inte skär den givna linjen (Playfairs axiom).
- Om två linjer är parallella mot en tredje linje, är de parallella mot varandra.
- Om alternativa inre vinklar vid en transversal är lika så är linjerna parallella.
Dessa påståenden är inte sanna i samma form i icke‑euklidiska geometrier. I hyperbolisk geometri är triangelns vinkelsumma mindre än 180°, i elliptisk (spherical) geometri är den större än 180°.
Icke‑euklidiska geometrier och modeller
Genom att ersätta parallellpostulatet med ett annat antagande får man olika geometriska världar:
- Hyperbolisk geometri: Genom en punkt utanför en linje går minst två olikartade linjer som inte skär den givna linjen. Detta leder till bland annat att triangelns vinkelsumma är mindre än 180°. Modeller: Poincarés disk, Poincarés övre halvplan, Beltrami–Klein.
- Elliptisk (sferisk) geometri: Inga parallella linjer existerar — alla "räta" linjer (stora cirklar på en sfär) skär varandra. Triangelns vinkelsumma är större än 180°.
Beltramimodellen och Poincarémodellerna visade att om den euklidiska geometrin är konsistent, så är hyperbolisk geometrin också det. Detta fastställde parallellpostulatets oberoende av de andra euklidiska axiomen.
Var används begreppet idag?
Parallellpostulatet är fortfarande centralt i undervisning av klassisk geometri, men modern geometri och matematik undervisar ofta både euklidiska och icke‑euklidiska modeller för att ge en bredare bild av möjligheterna och konsekvenserna av olika axiomatiska val. Inom relativitetsteori och differentialgeometri används begrepp om krökning i stället för det enkla parallellbegreppet från Euklides, eftersom rumtiden där är icke‑euklidisk.
Sammanfattning
- Parallellpostulatet är Euklids femte postulat och ett fundament i klassisk euklidisk geometri.
- Det finns flera ekvivalenta formuleringar, där Playfairs axiom är den vanligaste moderna varianten.
- Historiska försök att härleda postulatet från de andra axiomen misslyckades och ledde till upptäckten av konsekventa icke‑euklidiska geometrier.
- Konsekvenserna av att ändra eller slopa parallellpostulatet visar hur känsliga geometriska satser är för de grundläggande antagandena.
Den geometri som följer alla Euklids axiom kallas euklidisk geometri. Geometrier som inte följer alla Euklids axiom kallas icke-euklidisk geometri, och studiet av dessa gav upphov till stora framsteg inom matematiken under 1800‑talet och framåt.
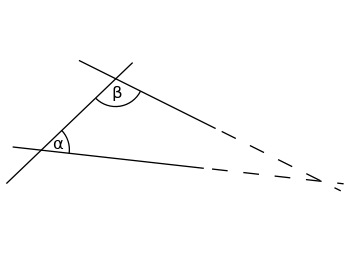
Om summan av de inre vinklarna α (alfa) och β (beta) är mindre än 180° kommer de två linjerna att skära varandra någonstans, om båda förlängs till oändligheten.
Historia
Vissa matematiker ansåg att Euklides femte postulat var mycket längre och mer komplicerat än de fyra andra postulaten. Många av dem trodde att det kunde bevisas utifrån de andra enklare axiomen. Några matematiker meddelade att de hade bevisat satsen från de enklare postulaten, men alla visade sig ha fel.
Playfairs axiom
En annan nyare sats som kallas Playfairs axiom liknar Euklids femte postulat. Det säger att:
Om du har en rät linje och en punkt som inte ligger på linjen kan du bara dra en rät linje genom denna punkt som inte möter den andra rät linjen.
Matematikerna upptäckte faktiskt att detta axiom inte bara liknar Euklids femte postulat utan har exakt samma innebörd. Matematiskt sett kallas de två påståendena för "likvärdiga" påståenden. I dag används Playfairs axiom oftare av matematiker än Euklids ursprungliga parallella postulat.
Icke-euklidisk geometri
Så småningom försökte några matematiker bygga nya geometrier utan att använda axiomet. En typ av icke-euklidisk geometri kallas elliptisk geometri. I elliptisk geometri ersätts parallellpostulatet med ett axiom som säger att:
Med en rät linje och en punkt som inte ligger på linjen kan du inte rita en rät linje genom denna punkt som inte till slut korsar den andra rät linjen.
Matematikerna upptäckte att när de ersatte Euklids femte postulat med detta axiom kunde de fortfarande bevisa många av Euklids andra satser. Ett sätt att föreställa sig elliptisk geometri är att tänka på ytan av en jordglob. På en jordglob verkar längdlinjerna vara parallella vid ekvatorn, men de möts alla vid polerna. I slutet av 1800-talet visade sig den elliptiska geometrin vara konsekvent. Detta bevisade att Euklids femte postulat inte var oberoende av de andra postulaten. Efter detta slutade matematikerna för det mesta att försöka bevisa det femte postulatet utifrån de fyra andra postulaten. I stället började många matematiker studera andra geometrier som inte följer Euklids femte postulat.
Ett annat axiom som matematiker ibland ersätter Euklids femte axiom med är följande:
Om du har en rät linje och en punkt som inte ligger på linjen, kan du rita minst två räta linjer genom denna punkt som inte korsar den andra räta linjen.
Detta kallas hyperbolisk geometri.
En annan geometri tar helt enkelt bort Euklids femte postulat och ersätter det inte med något annat. Detta kallas neutral geometri eller absolut geometri.
Sök