Pi | matematisk konstant som är förhållandet mellan en cirkels omkrets och dess diameter

Grunderna

Definition

π definieras vanligen som förhållandet mellan en cirkels omkrets C och dess diameter d:

π = C d . {\displaystyle \pi ={\frac {C}{d}}}.}

Ungefärligt värde

Pi skrivs ofta som π, eller den grekiska bokstaven π som en förkortning. Pi är också ett irrationellt tal, vilket innebär att det inte kan skrivas som ett bråk ( a b {\displaystyle a \over b} ), där "a" och "b" är heltal (hela tal). Detta innebär i princip att siffrorna i pi som står till höger om decimalvärdet går i evighet - utan att upprepas i ett mönster - och att det är omöjligt att skriva det exakta värdet av pi som ett tal. Pi kan endast approximeras eller mätas till ett värde som är tillräckligt nära för praktiska ändamål.

Ett värde nära pi är 3,1415926535358979323838462643... Ett vanligt bråk som närmar sig pi är 22 / 7 {\displaystyle 22/7} , vilket ger ungefär 3,14285714. Denna approximation är 0,04 % från det sanna värdet av pi. Även om denna approximation accepteras för de flesta av dess användningsområden i det verkliga livet, är bråket 355 / 113 {\displaystyle 355/113} mer exakt (ger ungefär 3,14159292) och kan användas när ett värde närmare pi behövs. Datorer kan användas för att få bättre approximationer av pi.

I mars 2019 räknade Emma Haruka Iwao ut värdet av pi till 31,4 biljoner siffror.

 
En cirkels omkrets är något mer än tre gånger så lång som dess diameter. Det exakta förhållandet kallas π .  


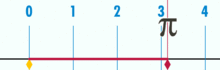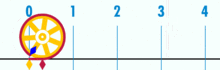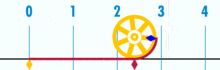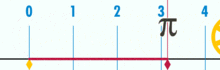
Ett diagram som visar hur π kan hittas med hjälp av en cirkel med en diameter på ett. Cirkelns omkrets är π.  

Historia

Matematiker har känt till pi i tusentals år, eftersom de har arbetat med cirklar lika länge. Civilisationer så gamla som babylonierna har kunnat approximera pi till många siffror, till exempel bråket 25/8 och 256/81. De flesta historiker tror att de gamla egyptierna inte hade något begrepp om π och att överensstämmelsen är en tillfällighet.

Den första skriftliga hänvisningen till pi är från 1900 f.Kr. Omkring 1650 f.Kr. angav egyptiern Ahmes ett värde i Rhindpapyrus. Babylonierna kunde konstatera att värdet pi var något större än 3 genom att helt enkelt göra en stor cirkel och sedan fästa en repbit på omkretsen och diametern, notera avstånden mellan dem och sedan dividera omkretsen med diametern.

Kunskapen om talet pi gick tillbaka till Europa och kom i händerna på hebréerna, som gjorde talet viktigt i en del av Bibeln som kallas Gamla testamentet. Efter detta var det vanligaste sättet att försöka hitta pi att rita en form med många sidor inuti en cirkel och använda formens area för att hitta pi. Den grekiske filosofen Archimedes använde till exempel en polygonform med 96 sidor för att hitta värdet på pi, men kineserna kunde år 500 e.Kr. använda en polygonform med 16 384 sidor för att hitta värdet på pi. Grekerna, som Anaxagoras av Clazomenae, var också upptagna med att ta reda på andra egenskaper hos cirkeln, till exempel hur man gör kvadrater av cirklar och hur man kvadrerar talet pi. Sedan dess har många människor försökt ta reda på mer och mer exakta värden på pi.

En historia om pi
Filosof	Datum	Tillnärmning
Claudius Ptolemaios	omkring 150 e.Kr.	3.1416
Zu Chongzhi	430-501 CE	3.1415929203
al-Khwarizmi	omkring 800 e.Kr.	3.1416
al-Kashi	omkring 1430	3.14159265358979
Viète	1540-1603	3.141592654
Roomen	1561-1615	3.14159265358979323
Van Ceulen	omkring 1600	3.14159265358979323846264338327950288

På 1500-talet kom man fram till allt bättre sätt att räkna ut pi, till exempel den komplicerade formel som den franske advokaten François Viète utvecklade. Den grekiska symbolen "π" användes för första gången i en uppsats skriven 1706 av William Jones.

En matematiker vid namn Lambert visade också 1761 att talet pi är irrationellt, det vill säga att det inte kan skrivas som en bråkdel enligt normala normer. En annan matematiker vid namn Lindeman kunde också 1882 visa att pi ingick i den grupp av tal som kallas transcendentala, vilket är tal som inte kan vara lösningen på en polynomisk ekvation.

Pi kan också användas för att räkna ut många andra saker än cirklar. Pi:s egenskaper har gjort det möjligt att använda det inom många andra matematiska områden än geometri, studiet av former. Några av dessa områden är komplex analys, trigonometri och serier.

 

Pi i verkligheten

Det finns olika sätt att beräkna många siffror av π. Detta är dock av begränsad nytta.

Pi kan ibland användas för att beräkna arean eller omkretsen av en cirkel. För att hitta en cirkels omkrets används formeln C (omkrets) = π × (diameter). För att beräkna arean av en cirkel använder du formeln π (radie²). Denna formel skrivs ibland som A = π r 2 {\displaystyle A=\pi r^{2}} , där r är variabeln för radien i en cirkel och A är variabeln för cirkelns area.

Att beräkna omkretsen av en cirkel med ett fel på 1 mm:

• 4 siffror behövs för en radie på 30 meter.
• 10 siffror för en radie som är lika med jordens.
• 15 siffror för en radie som är lika med avståndet från jorden till solen.
• 20 siffror för en radie som är lika med avståndet från jorden till Polaris.

Den 14 mars firas vanligen som Pi-dagen, eftersom den 14 mars också skrivs som 3/14, vilket representerar de tre första siffrorna 3,14 i approximationen av pi. Pi-dagen startade under 2001.

 

Relaterade sidor

• Förteckning över nummer
• Irrationella tal
• Kvadratrot av 2
• Det gyllene snittet
• E (matematisk konstant)
• Att göra cirkeln fyrkantig
• Transcendentalt tal