Ampère's cirkuital lag

Ursprunglig Ampères cirkulationslag

Lagen relaterar magnetfält till elektriska strömmar som producerar dem. En forskare kan använda Amperes lag för att bestämma magnetfältet i samband med en given ström eller strömmen i samband med ett givet magnetfält, om det inte finns något elektriskt fält som förändras i tiden. I sin ursprungliga form relaterar Ampere's cirkulära lag magnetfältet till dess elektriska strömkälla. Lagen kan skrivas i två former, "integralformen" och "differentialformen". Formerna är likvärdiga och relateras genom Kelvin-Stokes-satsen. Den kan också skrivas i termer av antingen B- eller H-magnetiska fält. Även här är de två formerna likvärdiga (se avsnittet "bevis" nedan).

Det är nu känt att Ampères cirkulationslag är en korrekt fysikalisk lag i en magnetostatisk situation: Systemet är statiskt, utom möjligen för kontinuerliga, stabila strömmar i slutna kretsar. I alla andra fall är lagen felaktig om inte Maxwells korrigering inkluderas (se nedan).

Integralform

I SI-enheter (versionen i cgs-enheter finns i ett senare avsnitt) är "integralformen" av den ursprungliga Ampères cirkulationslag:

• ∮ C B ⋅ d ℓ = μ 0 ∬ S J ⋅ d S {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}\iint _{S}\mathbf {J} \cdot \mathrm {d} \mathbf {S} }
• ∮ C H ⋅ d ℓ = ∬ S J f ⋅ d S {\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\mathbf {J} _{\mathrm {f} }\cdot \mathrm {d} \mathbf {S} }

eller på motsvarande sätt,

• ∮ C B ⋅ d ℓ = μ 0 I e n c {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\mu _{0}I_{\mathrm {enc} }}
• ∮ C H ⋅ d ℓ = I f , e n c {\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=I_{\mathrm {f,enc} }}

där

• - är vektorns punktprodukt, ∮ C {\displaystyle \textstyle \oint _{C}} är det slutna linjeintegralet runt den slutna kurvan C, ∬ S {\displaystyle \textstyle \iint _{S}} betecknar ett integral över den yta S som omges av kurvan C (det dubbla integraltecknet är tänkt att beteckna att integralen är tvådimensionell till sin natur);
• B är det magnetiska B-fältet i teslas, H är det magnetiska H-fältet i ampere per meter;
• I_f,enc är den fria nettoströmmen som tränger igenom ytan S, I_enc är den totala nettoströmmen som tränger igenom ytan S, inklusive både fri och bunden ström.
• J_f är den fria strömtätheten genom den yta S som omges av kurvan C, J är den totala strömtätheten genom den yta S som omges av kurvan C, inklusive både fri och bunden ström;
• dℓ är ett infinitesimalt element (en differential) av kurvan C (dvs. en vektor vars storlek är lika med längden på det infinitesimala linjeledet och vars riktning ges av tangenten till kurvan C), dS är vektorns area av ett infinitesimalt element av ytan S (dvs. en vektor vars storlek är lika med arean av det infinitesimala ytelementet och vars riktning är normal till ytan S. Normalkanalen måste motsvara orienteringen av C enligt högerhandregeln);
• μ₀ är den magnetiska konstanten;

Se nedan för ytterligare förklaring av kurvan C och ytan S. Det finns ett antal tvetydigheter i ovanstående definitioner som kräver ett förtydligande och ett val av konvention.

För det första är tre av dessa termer förknippade med teckentvetydigheter: linjeintegralen ∮ C {\displaystyle \textstyle \oint _{C}} skulle kunna gå runt slingan i båda riktningarna (med eller moturs); vektorområdet dS skulle kunna peka i någon av de två riktningar som är normala för ytan; och I_enc är nettoströmmen som passerar genom ytan S, vilket innebär att strömmen som passerar genom den ena riktningen minus strömmen i den andra riktningen - men båda riktningarna kan väljas som positiva. Dessa tvetydigheter löses med hjälp av den högra regeln: Med högerhandens handflata mot integrationsytan och pekfingret pekar i linjeintegrationens riktning, pekar den utsträckta tummen i den riktning som måste väljas för vektorytan dS. Även den ström som går i samma riktning som dS måste räknas som positiv. Regeln för högerhandens grepp kan också användas för att bestämma tecknen.

För det andra finns det oändligt många möjliga ytor S som har kurvan C som gräns. (Tänk dig en tvålfilm på en trådslinga, som kan deformeras genom att flytta tråden). Vilken av dessa ytor ska väljas? Om slingan till exempel inte ligger i ett enda plan finns det inget självklart val. Svaret är att det inte spelar någon roll; det kan bevisas att vilken yta som helst med gräns C kan väljas.

Differentialform

Med hjälp av Kelvin-Stokes-satsen kan denna ekvation också skrivas i en "differentiell form". Återigen gäller denna ekvation endast i det fall då det elektriska fältet är konstant i tiden; se nedan för den mer allmänna formen. I SI-enheter lyder ekvationen:

∇ × B = μ 0 J {\displaystyle \mathbf {\nabla } \times \mathbf {B} =\mu _{0}\mathbf {J} }

∇ × H = J f {\displaystyle \mathbf {\nabla } \times \mathbf {H} =\mathbf {J_{f}} }

där

∇ × {\displaystyle \mathbf {\nabla } \times \!\ } är curloperatorn.  

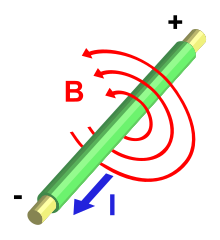
En elektrisk ström producerar ett magnetfält.  

Anmärkning om fri ström kontra bunden ström

Den elektriska ström som uppstår i de enklaste situationer som finns i läroböckerna skulle klassificeras som "fri ström". Lagen kan till exempel tillämpas på den ström som passerar genom en tråd eller ett batteri. Däremot uppstår "bunden ström" i samband med bulkmaterial som kan magnetiseras och/eller polariseras. (Alla material kan göra det i viss utsträckning.)

När ett material magnetiseras (t.ex. genom att placera det i ett yttre magnetfält) förblir elektronerna bundna till sina respektive atomer, men beter sig som om de kretsar runt kärnan i en viss riktning, vilket skapar en mikroskopisk ström. När strömmarna från alla dessa atomer läggs samman skapar de samma effekt som en makroskopisk ström, som ständigt cirkulerar runt det magnetiserade föremålet. Denna magnetiseringsström J_M är ett bidrag till "bunden ström".

Den andra källan till bunden ström är bunden laddning. När ett elektriskt fält tillämpas kan de positiva och negativa bundna laddningarna separeras över atomära avstånd i polariserbara material, och när de bundna laddningarna rör sig förändras polariseringen, vilket skapar ett annat bidrag till den "bundna strömmen", polariseringsströmmen J_P .

Den totala strömtätheten J som beror på fria och bundna laddningar är då:

J = J f + J M + J P , {\displaystyle \mathbf {J} =\mathbf {J_{f}+J_{M}+J_{P}} \ ,}

med J_f den "fria" eller "ledande" strömtätheten.

All ström är i grunden lika, mikroskopiskt sett. Det finns ofta praktiska skäl för att behandla bunden ström annorlunda än fri ström. Den bundna strömmen uppstår till exempel vanligtvis i atomära dimensioner, och man kanske vill dra nytta av en enklare teori som är avsedd för större dimensioner. Resultatet blir att den mer mikroskopiska Ampères lag, uttryckt i termer av B och den mikroskopiska strömmen (som omfattar fria, magnetiserings- och polarisationsströmmar), ibland sätts in i den ekvivalenta formen nedan i termer av endast H och den fria strömmen. För en detaljerad definition av fri ström och bunden ström och beviset för att de två formuleringarna är likvärdiga, se avsnittet "bevis" nedan.

 

Brister i den ursprungliga formuleringen av Ampères cirkulationslag

Två frågor om Ampères lag är viktiga. För det första finns det en fråga om kontinuitetsekvationen för elektrisk laddning. Det finns en sats i vektorkalkyl som säger att divergensen av en curl alltid måste vara noll. Därför är

∇ ⋅ ( ∇ × B ) = 0 {\displaystyle \nabla \cdot (\nabla \times {\mathbf {B}})=0}

och den ursprungliga Ampères lag innebär alltså att

∇ ⋅ J = 0 {\displaystyle \nabla \cdot {\mathbf {J}}=0}

Men i allmänhet

∇ ⋅ J = - ∂ ρ ρ ∂ t {\displaystyle \nabla \cdot {\mathbf {J}}=-{\frac {\partial \rho }{\partial t}}}

som inte är noll för en tidsvarierande laddningstäthet. Ett exempel är en kondensatorkrets där det finns tidsvarierande laddningstätheter på plattorna.

För det andra finns det en fråga om elektromagnetiska vågors utbredning. I det fria utrymmet, där

J = 0 {\displaystyle {\mathbf {J}}={\mathbf {0}}}

Ampères lag innebär att

∇ × B = 0 {\displaystyle \nabla \times {\mathbf {B}}={\mathbf {0}}}}

utan istället

∇ × B = - 1 c 2 ∂ E ∂ t {\displaystyle \nabla \times {\mathbf {B}}=-{\frac {1}{c^{2}}}}{\frac {\partial {\mathbf {E}}}}{\partial t}}}

För att behandla dessa situationer måste bidraget från förskjutningsströmmen läggas till strömtermen i Ampères lag.

James Clerk Maxwell uppfattade förskjutningsströmmen som en polarisationsström i det dielektriska virvelhavet, som han använde för att modellera magnetfältet med vatten (hydrodynamiskt) och med mekaniska system (mekaniskt). Han lade till denna förskjutningsström till Ampères cirkulära lag i ekvation (112) i sin artikel On Physical Lines of Force från 1861.

Förskjutningsström

I det fria rummet är förskjutningsströmmen relaterad till tidshastigheten för förändring av det elektriska fältet.

I ett dielektrikum finns ovanstående bidrag till förskjutningsströmmen också, men ett större bidrag till förskjutningsströmmen är relaterat till polariseringen av de enskilda molekylerna i det dielektriska materialet. Även om laddningar inte kan flöda fritt i ett dielektrikum kan laddningarna i molekylerna förflytta sig en aning under påverkan av ett elektriskt fält. De positiva och negativa laddningarna i molekylerna separeras under det applicerade fältet, vilket orsakar en ökning av polarisationstillståndet, uttryckt som polarisationsdensiteten P. Ett förändrat polarisationstillstånd är likvärdigt med en ström.

Båda bidragen till förskjutningsströmmen kombineras genom att förskjutningsströmmen definieras som:

J D = ∂ ∂ t D ( r , t ) , {\displaystyle \mathbf {J_{D}} ={\frac {\partial }{\partial t}}\mathbf {D} ({\boldsymbol {r}},\ t)\ ,}

där det elektriska förskjutningsfältet definieras som:

D = ε 0 E + P = ε 0 ε r E , {\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} =\varepsilon _{0}\varepsilon _{r}\mathbf {E} \ ,}

där ε₀ är den elektriska konstanten, ε_r den relativa statiska permittiviteten och P är polarisationstätheten. Om man ersätter denna form för D i uttrycket för förskjutningsströmmen har den två komponenter:

J D = ε 0 ∂ E ∂ t + ∂ P ∂ t . {\displaystyle \mathbf {J} _{\mathrm {D} }=\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}+{\frac {\partial \mathbf {P} }{\partial t}}. }

Den första termen på höger sida finns överallt, även i ett vakuum. Den innebär ingen faktisk laddningsrörelse, men den har ändå ett tillhörande magnetfält, som om den vore en faktisk ström. Vissa författare använder namnet förskjutningsström för endast detta bidrag.

Den andra termen på höger sida är förskjutningsströmmen enligt Maxwells ursprungliga uppfattning, som är förknippad med polariseringen av de enskilda molekylerna i det dielektriska materialet.

Maxwells ursprungliga förklaring till förskjutningsströmmar fokuserade på den situation som uppstår i dielektriska medier. I den moderna tiden efter etern har begreppet utvidgats till att även gälla situationer utan materiella medier, t.ex. vakuumet mellan plattorna i en laddande vakuumkondensator. Förskjutningsströmmen är motiverad idag eftersom den uppfyller flera krav på en elektromagnetisk teori: korrekt förutsägelse av magnetfält i områden där ingen fri ström flyter, förutsägelse av vågutbredning av elektromagnetiska fält och bevarande av elektrisk laddning i fall där laddningstätheten är tidsvarierande. För en utförligare diskussion se Förskjutningsström.

 

Utvidgning av den ursprungliga lagen: Maxwell-Ampère-ekvationen

Ampères ekvation utvidgades genom att inkludera polariseringsströmmen, vilket avhjälpte den begränsade tillämpligheten av Ampères ursprungliga cirkulationslag.

Om man behandlar fria laddningar separat från bundna laddningar är Ampères ekvation inklusive Maxwells korrigering i termer av H-fältet (H-fältet används eftersom det inkluderar magnetiseringsströmmarna, så J_M förekommer inte uttryckligen, se H-fältet och även Notera):

∮ C H ⋅ d ℓ = ∬ S ( J f + ∂ ∂ t D ) ⋅ d A {\displaystyle \oint _{C}\mathbf {H} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\left(\mathbf {J} _{\mathrm {f} }+{\frac {\partial }{\partial t}}\mathbf {D} \right)\cdot \mathrm {d} \mathbf {A} }

(integralform), där H är det magnetiska H-fältet (även kallat "hjälpmagnetfält", "magnetfältsintensitet" eller bara "magnetfält"), D är det elektriska förskjutningsfältet och J_f är den inneslutna ledningsströmmen eller den fria strömtätheten. I differentiell form,

∇ × H = J f + ∂ ∂ t D . {\displaystyle \mathbf {\nabla } \times \mathbf {H} =\mathbf {J} _{\mathrm {f} }+{\frac {\partial }{\partial t}}\mathbf {D} \ . }

Om man däremot behandlar alla laddningar på samma sätt (oavsett om de är bundna eller fria laddningar) är den generaliserade Ampèreekvationen (även kallad Maxwell-Ampèreekvationen) (se avsnittet "bevis" nedan):

∮ C B ⋅ d ℓ = ∬ S ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) ⋅ d A {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}=\iint _{S}\left(\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E} \right)\cdot \mathrm {d} \mathbf {A} }

i integralform. I differentialform,

∇ × B = ( μ 0 J + μ 0 ϵ 0 ∂ ∂ t E ) . {\displaystyle \mathbf {\nabla } \times \mathbf {B} =(\mu _{0}\mathbf {J} +\mu _{0}\epsilon _{0}{\frac {\partial }{\partial t}}\mathbf {E} )\ . }

I båda formerna omfattar J magnetiseringsströmtäthet samt lednings- och polarisationsströmtätheter. Det innebär att strömtätheten på höger sida av Ampère-Maxwell-ekvationen är:

J f + J D + J M = J f + J P + J M + ε 0 ∂ E ∂ t = J + ε 0 ∂ E ∂ t , {\displaystyle \mathbf {J_{f}+J_{D}+J_{M}} =\mathbf {J_{f}+J_{P}+J_{M}} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}=\mathbf {J}} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\ ,}

där strömtätheten J_D är förskjutningsströmmen och J är det bidrag till strömtätheten som faktiskt beror på förflyttning av laddningar, både fria och bundna. Eftersom ∇ - D = ρ är problemet med kontinuiteten i Ampères ursprungliga formulering inte längre något problem. På grund av termen i ε₀ ∂E / ∂t är vågutbredning i det fria rummet nu möjlig.

Med tillägget av förskjutningsströmmen kunde Maxwell (korrekt) anta att ljuset var en form av elektromagnetisk våg. Se elektromagnetisk vågekvation för en diskussion om denna viktiga upptäckt.

Bevis på likvärdighet

Bevis för att formuleringarna av Ampères lag i termer av fri ström är likvärdiga med formuleringarna som omfattar totalströmmen.

I detta bevis kommer vi att visa att ekvationen ∇ × H = J f + ∂ D ∂ t {\displaystyle \nabla \times \mathbf {H} =\mathbf {J} _{f}+{\frac {\partial \mathbf {D} }{\partial t}}}} är likvärdig med ekvationen ∇ × B / μ 0 = J + ϵ 0 ∂ E ∂ t {\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {J} +\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}} Observera att vi bara behandlar differentialformerna, inte integralformerna, men det räcker eftersom differential- och integralformerna är likvärdiga i varje fall, enligt Kelvin-Stokes-satsen. Vi introducerar polarisationsdensiteten P, som har följande förhållande till E och D: D = ϵ 0 E + P {\displaystyle \mathbf {D} =\epsilon _{0}\mathbf {E} +\mathbf {P} } Därefter introducerar vi magnetiseringstätheten M, som har följande samband med B och H: B / μ 0 = H + M {\displaystyle \mathbf {B} /\mu _{0}=\mathbf {H} +\mathbf {M} } och följande förhållande till den bundna strömmen: J b o u n d = ∇ × M + ∂ P ∂ t , {\displaystyle \mathbf {J} _{\mathrm {bound} }=\nabla \times \mathbf {M} +{\frac {\partial \mathbf {P} }{\partial t}}}\ ,} = J M + J P , {\displaystyle =\mathbf {J} _{\mathrm {M} }+\mathbf {J} _{\mathrm {P}} }\ ,} där J M = ∇ × M , {\displaystyle \mathbf {J} _{\mathrm {M} }=\nabla \times \mathbf {M} \ ,} kallas magnetiseringsströmtätheten, och J P = ∂ P ∂ t , {\displaystyle \mathbf {J} _{\mathrm {P} }={\frac {\partial \mathbf {P} }{\partial t}}} ,} är polarisationsströmtätheten. Med ekvationen för B: ∇ × B / μ 0 = ∇ × ( H + M ) {\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {\nabla } \times \left(\mathbf {H+M} \right)} } = ∇ × H + J M {\displaystyle =\mathbf {\nabla } \times \mathbf {H} +\mathbf {J_{M}} } = J f + J P + ε 0 ∂ E ∂ t + J M {\displaystyle =\mathbf {J_{f}} +\mathbf {J_{P}} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}+\mathbf {J_{M}} } Därför hänvisar vi till definitionen av den bundna strömmen: ∇ × B / μ 0 = J f + J b o u n d + ε 0 ∂ E ∂ t {\displaystyle \mathbf {\nabla } \times \mathbf {B} /\mu _{0}=\mathbf {J_{f}} +\mathbf {J} _{\mathrm {bound} }+\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}} = J + ε 0 ∂ E ∂ t , {\displaystyle =\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}}\ ,} som skulle visas.

 

Ampères lag i cgs-enheter

I cgs-enheter lyder ekvationens integralform, inklusive Maxwells korrigering, som följer

∮ C B ⋅ d ℓ = 1 c ∬ S ( 4 π J + ∂ E ∂ t ) ⋅ d S {\displaystyle \oint _{C}\mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }}={\frac {1}{c}}\iint _{S}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}}\right)\cdot \mathrm {d} \mathbf {S} }

där c är ljusets hastighet.

Den differentiella formen av ekvationen (återigen inklusive Maxwells korrigering) är

∇ × B = 1 c ( 4 π J + ∂ E ∂ t ) . {\displaystyle \mathbf {\nabla } \times \mathbf {B} ={\frac {1}{c}}\left(4\pi \mathbf {J} +{\frac {\partial \mathbf {E} }{\partial t}}\right). }  

Relaterade sidor