Punktprodukt

Definition

Punktprodukten av två vektorer a = [a₁ , a₂ , ..., a_n ] och b = [b₁ , b₂ , ..., b_n ] definieras som:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

där Σ betecknar summering (summan av alla termer) och n är vektorrummets dimension.

I dimension 2 är punktprodukten av vektorerna [a,b] och [c,d] ac + bd. På samma sätt är punktprodukten av vektorerna [a,b,c] och [d,e,f] i dimension 3 ad + be + cf. Exempelvis är punktprodukten av två tredimensionella vektorer [1, 3, -5] och [4, -2, -1]

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Geometrisk tolkning

I euklidisk geometri är punktprodukten, längden och vinkeln relaterade till varandra. För en vektor a är punktprodukten a - a kvadraten på längden av a, eller

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}}

där ||a|| betecknar längden (storleken) av a. Mer allmänt, om b är en annan vektor

a ⋅ b = ‖ a ‖ ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\\\\,\left\|\mathbf {b} \right\|\cos \theta \,}

där ||a|| och ||b|| anger längden på a och b och θ är vinkeln mellan dem.

Denna formel kan omformas för att bestämma storleken på vinkeln mellan två vektorer som inte är noll:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}}right\\}}\}right)}

Man kan också först omvandla vektorerna till enhetsvektorer genom att dividera med deras magnitud:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\}}}

Då ges vinkeln θ av följande formel

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}}\cdot {\boldsymbol {\hat {b}}})}

Eftersom cosinus av 90° är noll, är punktprodukten av två ortogonala (vinkelräta) vektorer alltid noll. Dessutom kan två vektorer betraktas som ortogonala om och endast om deras punktprodukt är noll och de båda har en längd som inte är noll. Denna egenskap ger en enkel metod för att testa villkoret för ortogonalitet.

Ibland används dessa egenskaper också för att definiera punktprodukten, särskilt i två och tre dimensioner; denna definition är likvärdig med den ovan nämnda. För högre dimensioner kan formeln användas för att definiera begreppet vinkel.

De geometriska egenskaperna bygger på att basen är ortonormal, dvs. består av parvis vinkelräta vektorer med enhetlig längd.

Skalärprojektion

Om både a och b har längden ett (dvs. de är enhetsvektorer) är deras punktprodukt helt enkelt cosinus av vinkeln mellan dem.

Om endast b är en enhetsvektor ger punktprodukten a - b |a| cos(θ), dvs. storleken på projektionen av a i riktning mot b, med ett minustecken om riktningen är motsatt. Detta kallas den skalära projektionen av a på b, eller den skalära komponenten av a i riktning mot b (se figuren). Denna egenskap hos punktprodukten har flera användbara tillämpningar (se till exempel nästa avsnitt).

Om varken a eller b är en enhetsvektor är storleken på projektionen av a i riktning mot b till exempel a - (b / |b|) eftersom enhetsvektorn i riktning mot b är b / |b|.

Rotation

En rotation av den ortonormala bas som vektorn a representeras av erhålls genom en multiplikation av a med en rotationsmatris R. Denna matrismultiplikation är bara en kompakt representation av en sekvens av punktprodukter.

Låt till exempel

• B₁ = {x, y, z} och B₂ = {u, v, w} är två olika ortonormala baser av samma rum R³ , där B₂ erhålls genom att bara rotera B₁ ,
• a₁ = (a_x , a_y , a_z ) representerar vektor a i termer av B ,₁
• a₂ = (a_u , a_v , a_w ) representerar samma vektor i termer av den roterade basen B₂ ,
• u₁ , v₁ , w₁ är de roterade basvektorerna u, v, w som representeras i termer av B₁ .

Därefter utförs rotationen från B₁ till B₂ på följande sätt:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}\\{mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\a_{v}\\\a_{w}\end{bmatrix}}. }

Observera att rotationsmatrisen R sätts samman genom att använda de roterade basvektorerna u₁ , v₁ , w₁ som rader, och dessa vektorer är enhetsvektorer. Per definition består Ra₁ av en sekvens av punktprodukter mellan var och en av de tre raderna i R och vektorn a₁ . Var och en av dessa punktprodukter bestämmer en skalär komponent av a i riktning mot en roterad basvektor (se föregående avsnitt).

Om₁ är en radvektor, snarare än en kolumnvektor, måste R innehålla de roterade basvektorerna i sina kolumner och eftermultiplicera₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

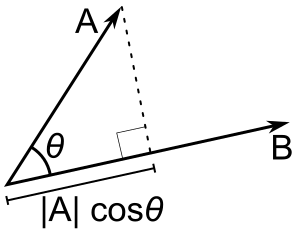
A - B = |A| |B| cos(θ). |A| cos(θ) är den skalära projektionen av A på B.

Fysik

Inom fysiken är magnitud en skalär i fysikalisk mening, dvs. en fysikalisk kvantitet som är oberoende av koordinatsystemet och som uttrycks som en produkt av ett numeriskt värde och en fysisk enhet, inte bara ett tal. Punktprodukten är också en skalär i denna mening, given genom formeln, oberoende av koordinatsystemet. Exempel:

• Mekaniskt arbete är punktprodukten av kraft- och förskjutningsvektorer.
• Det magnetiska flödet är punktprodukten av magnetfältet och areavektorerna.
• Volymflödet är punktprodukten av vätskans hastighet och areavektorerna.

Egenskaper

Följande egenskaper gäller om a, b och c är reella vektorer och r är en skalär.

Punktprodukten är kommutativ:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Punktprodukten är distributiv över vektoraddition:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Punktprodukten är bilinjär:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

När den multipliceras med ett skalärt värde uppfyller punktprodukten kraven:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(de två sista egenskaperna följer av de två första).

Två vektorer a och b som inte är noll är vinkelräta om och endast om a - b = 0.

Till skillnad från multiplikation av vanliga tal, där om ab = ac, så är b alltid lika med c om inte a är noll, följer punktprodukten inte annulleringslagen:

Om a - b = a - c och a ≠ 0 kan vi skriva: a - (b - c) = 0 enligt distributiva lagen; resultatet ovan säger att detta bara betyder att a är vinkelrätt mot (b - c), vilket fortfarande gör att (b - c) ≠ 0, och därför b ≠ c.

Förutsatt att basen är ortonormal är punktprodukten invariant vid isometriska förändringar av basen: rotationer, reflektioner och kombinationer, med fast ursprung. Den ovan nämnda geometriska tolkningen bygger på denna egenskap. Med andra ord, för ett ortonormalt rum med valfritt antal dimensioner är punktprodukten invariant under en koordinattransformation baserad på en ortogonal matris. Detta motsvarar följande två villkor:

• Den nya basen är återigen ortonormal (dvs. den är ortonormal uttryckt i den gamla basen).
• De nya basvektorerna har samma längd som de gamla (dvs. enhetslängd i förhållande till den gamla basen).

Om a och b är funktioner är derivatan av a - b a' - b + a - b'.

Expansion av trippelprodukter

Detta är en mycket användbar identitet (även känd som Lagranges formel) som involverar punkt- och korsprodukten. Den skrivs som

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

vilket är lättare att komma ihåg som "BAC minus CAB", med tanke på vilka vektorer som är prickade tillsammans. Denna formel används ofta för att förenkla vektorberäkningar inom fysiken.

Bevis för den geometriska tolkningen

Betrakta elementet i R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Upprepad tillämpning av Pythagoras sats ger för dess längd |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Men det är samma sak som

v ⋅ v = v 1 2 + v 2 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

Vi drar alltså slutsatsen att om man tar punktprodukten av en vektor v med sig själv får man vektorns längd i kvadrat.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Betrakta nu två vektorer a och b som sträcker sig från ursprunget och som är åtskilda av en vinkel θ. En tredje vektor c kan definieras som

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}}\ \mathbf {a} -\mathbf {b} .\,}

vilket ger en triangel med sidorna a, b och c. Enligt cosinuslagen har vi följande

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} |\mathbf {b} |\cos \theta .\,}

Genom att ersätta de kvadrerade längderna med punktprodukter enligt Lemma 1 får vi följande resultat

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} (1)

Men eftersom c ≡ a - b, har vi också

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

som enligt fördelningslagen expanderar till

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

Genom att slå ihop de två c - c-ekvationerna (1) och (2) får vi följande resultat

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Genom att subtrahera a - a + b - b från båda sidorna och dividera med -2 får man

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Generalisering

Den inre produkten generaliserar punktprodukten till abstrakta vektorrum och betecknas vanligen med ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . På grund av den geometriska tolkningen av punktprodukten definieras normen ||a|| för en vektor a i ett sådant inre produktutrymme som

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

så att den generaliserar längden, och vinkeln θ mellan två vektorer a och b genom

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\\|\mathbf {a} \|\\,\|\mathbf {b} \|}}. }

I synnerhet anses två vektorer vara ortogonala om deras inre produkt är noll.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

För vektorer med komplexa poster skulle den givna definitionen av punktprodukten leda till helt andra geometriska egenskaper. Till exempel kan en vektors punktprodukt med sig själv vara ett godtyckligt komplext tal, och kan vara noll utan att vektorn är nollvektor; detta skulle i sin tur få allvarliga konsekvenser för begrepp som längd och vinkel. Många geometriska egenskaper kan räddas, till priset av att man ger upp de symmetriska och bilinjära egenskaperna hos skalarprodukten, genom att alternativt definiera

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

där b_i är den komplexa konjugaten av b_i . Skalarprodukten av varje vektor med sig själv är ett icke-negativt reellt tal, och den är icke-noll utom för nollvektorn. Denna skalarprodukt är dock inte linjär i b (utan snarare konjugerad linjär), och skalarprodukten är inte heller symmetrisk, eftersom

a ⋅ b = b ⋅ a ¯ {\\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}}} .

Denna typ av skalarprodukt är dock ganska användbar och leder till begreppen hermitisk form och allmänna inre produktutrymmen.

Frobenius inre produkt generaliserar punktprodukten till matriser. Den definieras som summan av produkterna av motsvarande komponenter i två matriser av samma storlek.

Generalisering till tensorer

Punktprodukten mellan en tensor av ordning n och en tensor av ordning m är en tensor av ordning n+m-2. Punktprodukten beräknas genom att multiplicera och summera över ett enda index i båda tensorer. Om A {\displaystyle \mathbf {A} } och B {\displaystyle \mathbf {B} } är två tensorer med elementrepresentation A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} och B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} är elementen i punktprodukten A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } ges av

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

Denna definition reduceras naturligt till den vanliga vektor-punktprodukten när den tillämpas på vektorer och matrismultiplikation när den tillämpas på matriser.

Ibland används en dubbel punktprodukt för att representera multiplikation och summering över två index. Den dubbla punktprodukten mellan två andra ordningens tensorer är en skalär.

Relaterade sidor

• Cauchy-Schwarz ojämlikhet
• Korsande produkt
• Matrismultiplikation
• Fysik