Ljusets hastighet (c) – definition, värde och roll i relativitetsteorin
Upptäck ljusets hastighet c — dess exakta värde, definition och avgörande roll i relativitetsteorin samt hur 299 792 458 m/s binder samman rum, tid och energi.
Ljusets hastighet i tomt utrymme är en universell fysikalisk konstant. Det betyder att den är densamma överallt i det tomma rummet och inte förändras med tiden. Fysiker använder ofta bokstaven c för att beteckna ljusets hastighet i tomt utrymme (vakuum). Den är per definition exakt 299 792 458 meter per sekund (983 571 056 fot per sekund). En foton (ljuspartikel) färdas med denna hastighet i vakuum.
Enligt den speciella relativitetsteorin är c den maximala hastighet som all energi, materia och fysisk information i universum kan färdas med. Det är hastigheten för alla masslösa partiklar, t.ex. fotoner, och tillhörande fält - inklusive elektromagnetisk strålning, t.ex. ljus - i ett vakuum.
Den nuvarande teorin förutsäger att den är gravitationens hastighet (dvs. gravitationsvågor). Sådana partiklar och vågor färdas med c oavsett källans rörelse eller observatörens tröghetsreferensram. I relativitetsteorin är c ett samband mellan rum och tid och förekommer i den berömda ekvationen för massa-energi-ekvivalens E = mc2.
Den speciella relativitetsteorin bygger på förutsägelsen, som hittills har bekräftats av observationer, att den uppmätta ljushastigheten i ett vakuum är densamma oavsett om ljuskällan och den person som utför mätningen rör sig i förhållande till varandra eller inte. Detta uttrycks ibland som att "ljusets hastighet är oberoende av referensramen".
Exakt värde och varför det är definierat så
c är per definition exakt 299 792 458 m/s. Denna exakta definition infördes 1983 när SI-systemet omdefinierade metern som den sträcka ljuset färdas i vakuum under 1/299 792 458 sekund. Syftet var att basera längdenhetsdefinitionen på en stabil fundamental konstant istället för på materiella standarder. Eftersom tidsmätningar (atomur) kan göras mycket exakt är detta en praktisk och stabil grund för hela måttenhetssystemet.
Vad det innebär för materia, energi och information
- Inga massiva partiklar når c: Partiklar med vilomassa kan aldrig uppnå ljusets hastighet eftersom den energi som krävs skulle bli oändlig.
- Masslösa partiklar färdas med c: Fotoner och andra masslösa excitationsmodi i fält (t.ex. vissa teoretiska gravitationskvanta) rör sig i vakuum med hastigheten c.
- Begränsning av informationsöverföring: c sätter en övre gräns för hur snabbt signaler och orsakssamband kan spridas. Det är grunden för begreppet kausalitet i fysiken.
Konsekvenser i relativitetsteorin
Att c är konstant leder till flera effekter som skiljer sig från klassisk (Newtonsk) intuition:
- Tidsdilatation: Rör sig ett objekt nära ljusets hastighet upplevs tiden för objektet som långsammare jämfört med en stillastående observatör (faktor γ = 1/√(1 − v²/c²)).
- Längdkontraktion: Avstånd i rörelseriktningen förkortas för ett objekt som rör sig relativt en observatör.
- Relativistisk massa/energi: Ett objekts energi ökar kraftigt med hastigheten; den välkända ekvationen E = mc2 visar att massa och energi är ekvivalenta. En mer allmän formel för rörelseenergi är E = γmc2.
Experiment och observationer som stödjer konstanten
Idén att ljusets hastighet är konstant oberoende av observatörens rörelse har verifierats i många experiment och observationer, bland annat:
- Michelson–Morley-experimentet (slutet av 1800-talet) visade ingen riktad skillnad i ljushastighet orsakad av jordens rörelse genom en hypotetisk "éter".
- Flera senare laboratorieexperiment och högprecisionstest, t.ex. Kennedy–Thorndike- och Ives–Stilwell-typer, stödjer speciell relativitet.
- Observationer av kosmiska partiklar och partikelacceleratorer visar att partiklar närmar sig men aldrig når c och att tidsdilatation för sönderfallstider stämmer med teorin.
Mätningar av gravitationsvågor och hastigheten för gravitation
Modern observationsdata har också kopplat gravitationens informationsspridning till c. Ett viktigt test var observationen av gravitationsvågan GW170817 från en sammansmältning av neutronstjärnor, tillsammans med en nästan samtidig gammablixt (gamma-ray burst). Skillnaden i ankomsttid för gravitationsvågor och elektromagnetisk strålning var mycket liten, vilket begränsar eventuell avvikelse i gravitationens hastighet till mycket små nivåer och stöder att gravitationsvågor färdas med hastigheten c inom mätosäkerheterna.
Praktiska konsekvenser och vardagliga exempel
- GPS-systemet måste ta hänsyn till relativistiska effekter (tidsdilatation både från satelitens hastighet och från gravitationen) för att ge korrekt positionsbestämning.
- I astronomi innebär den ändliga ljushastigheten att vi ser avlägsna objekt som de var tidigare i tiden. När vi observerar en stjärna eller en galax ser vi ett historiskt ljus, inte objektets nuvarande tillstånd.
Sammanfattning
Ljusets hastighet i vakuum, c, är en grundläggande konstant i modern fysik: den är exakt definierad som 299 792 458 m/s, är maximal hastighet för information och masslösa partiklar, och ligger till grund för relativitetsteorins beskrivning av rum och tid. Denna konstant påverkar allt från teoretiska konstruktioner i kosmologi till praktiska tekniska system som GPS.
Exempel
Detta beteende skiljer sig från våra vanliga föreställningar om rörelse, vilket visas i detta exempel:
George står på marken bredvid några tågspår (järnväg). Ett tåg rusar förbi i 48 km/h. George kastar en baseboll i 140 km/h i tågets riktning. Tom, en passagerare på tåget, har en anordning (som en radarpistol) för att mäta kasthastigheten. Eftersom Tom befinner sig på tåget rör han sig redan med 48 km/h i kastriktningen, så Tom mäter bollens hastighet som endast 97 km/h.
Med andra ord beror basebollens hastighet, som Tom mäter på tåget, på tågets hastighet.
I exemplet ovan rörde sig tåget med 1/3 av bollens hastighet, och bollens hastighet som mättes på tåget var 2/3 av kasthastigheten som mättes på marken.
Upprepa nu experimentet med ljus i stället för en baseboll, det vill säga George har en ficklampa i stället för att kasta en baseboll. George och Tom har båda samma apparater som mäter ljusets hastighet (i stället för radarpistolen i basebollexemplet).
George står på marken bredvid några tågspår. Ett tåg rusar förbi med 1/3 av ljusets hastighet. George blinkar med en ljusstråle i tågets riktning. George mäter ljusets hastighet till 186 282 miles per sekund (299 792 kilometer per sekund). Tom, en passagerare på tåget, mäter ljusstrålens hastighet. Vilken hastighet mäter Tom?
Intuitivt kan man tänka sig att hastigheten på ljuset från ficklampan som mäts på tåget borde vara 2/3 av den hastighet som mäts på marken, precis som hastigheten på basebollen var 2/3. Men i själva verket är den hastighet som mäts på tåget det fulla värdet, 186 282 miles per sekund (299 792 kilometer per sekund), inte 124 188 miles per sekund (199 861 kilometer per sekund).
Det låter omöjligt, men det är vad man mäter. En del av orsaken är att ljus är energi som agerar och rör sig på ett helt annat sätt än materia eller fasta föremål som en baseboll.
Maxwells ekvationer förutsade ljusets hastighet och bekräftade Michael Faradays idé att ljuset var en elektromagnetisk våg (ett sätt för energi att röra sig). Av dessa ekvationer framgår att ljusets hastighet är relaterad till inversen av kvadratroten av permittiviteten i det fria rummet, ε0, och permeabiliteten i det fria rummet, μ0:
c = 1 ε 0 μ 0 . {\displaystyle c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ . }
En konsekvens av detta faktum är att ingenting kan gå snabbare än ljusets hastighet. En annan konsekvens är att när det gäller föremål som har massa kommer ett föremål, oavsett hur mycket energi som används för att öka hastigheten, att komma närmare och närmare, men det kommer aldrig att nå ljusets hastighet. Dessa idéer upptäcktes i början av 1900-talet av Albert Einstein, vars arbete helt förändrade vår förståelse av ljuset.
Refraktionsindexet för ett klart material är förhållandet mellan ljusets hastighet i vakuum och ljusets hastighet i materialet.
Mätning
Rømer
Ole Christensen Rømer använde en astronomisk mätning för att göra den första kvantitativa uppskattningen av ljusets hastighet. Mätt från jorden är perioderna för månar som kretsar kring en avlägsen planet kortare när jorden närmar sig planeten än när jorden avlägsnar sig från den. Det avstånd som ljuset färdas från planeten (eller dess måne) till jorden är kortare när jorden befinner sig i den punkt i sin bana som ligger närmast planeten än när jorden befinner sig i den punkt i sin bana som ligger längst bort, och skillnaden i avstånd är diametern på jordens bana runt solen. Den observerade förändringen i månens omloppstid är i själva verket skillnaden i den tid det tar ljuset att färdas över det kortare eller längre avståndet. Rømer observerade denna effekt för Jupiters innersta måne Io, och han drog slutsatsen att ljuset tar 22 minuter på sig för att korsa diametern på jordens bana.
Bradley
En annan metod är att använda ljusets aberration, som upptäcktes och förklarades av James Bradley på 1700-talet. Denna effekt är resultatet av en vektorad addition av hastigheten hos ljuset som kommer från en avlägsen källa (t.ex. en stjärna) och hastigheten hos observatören (se diagrammet till höger). En observatör i rörelse ser alltså ljuset komma från en något annorlunda riktning och ser följaktligen källan i en position som är förskjuten från sin ursprungliga position. Eftersom riktningen för jordens hastighet ändras kontinuerligt när jorden kretsar runt solen, gör denna effekt att stjärnors skenbara position flyttas runt. Utifrån vinkelskillnaden i stjärnornas position är det möjligt att uttrycka ljusets hastighet i termer av jordens hastighet runt solen. Detta, med den kända längden på ett år, kan enkelt omvandlas till den tid som behövs för att färdas från solen till jorden. År 1729 använde Bradley denna metod för att härleda att ljuset färdas 10 210 gånger snabbare än jorden i dess omloppsbana (den moderna siffran är 10 066 gånger snabbare) eller, motsvarande, att det skulle ta ljuset 8 minuter och 12 sekunder att färdas från solen till jorden.
Modernt
Numera mäter man "ljustiden per avståndsenhet" - den omvända delen av c (1/c), uttryckt i sekunder per astronomisk enhet - genom att jämföra tiden för radiosignaler att nå olika rymdskepp i solsystemet. Rymdfarkosternas position beräknas utifrån solens och de olika planeternas gravitationseffekter. Genom att kombinera många sådana mätningar erhålls ett värde som passar bäst för ljustiden per avståndsenhet. Från och med 2009[uppdatering] är den bästa uppskattningen, som godkänts av Internationella astronomiska unionen (IAU), följande:
ljustid för en enhetssträcka: 499.004783836(10) s
c = 0,0020039888880410(4) AU/s
c = 173,144632674(3) AU/dag.
Den relativa osäkerheten i dessa mätningar är 0,02 delar per miljard (2×10-11), vilket motsvarar osäkerheten i jordbaserade längdmätningar genom interferometri. Eftersom metern definieras som den längd som ljuset tillryggalägger under ett visst tidsintervall, kan mätningen av ljustiden för en enhetsavstånd också tolkas som en mätning av längden av en AU i meter. Metern anses vara en enhet för egentlig längd, medan AU ofta används som en enhet för observerad längd i en viss referensram.
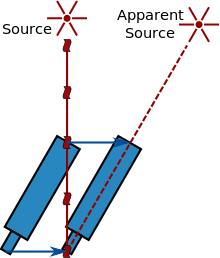
Aberration av ljus: Ljus från en avlägsen källa verkar komma från en annan plats i ett rörligt teleskop på grund av ljusets begränsade hastighet.
Praktiska effekter
Ljusets begränsade hastighet är ett stort hinder för långväga rymdresor. Om man antar att en resa till andra sidan Vintergatan skulle den totala tiden för ett meddelande och dess svar vara cirka 200 000 år. Ännu allvarligare är att inga rymdfarkoster kan färdas snabbare än ljuset, så all transport i galaktisk skala skulle i praktiken vara enkelriktad och ta mycket längre tid än vad någon modern civilisation har existerat.
Ljusets hastighet kan också vara ett problem på mycket korta avstånd. I superdatorer utgör ljusets hastighet en gräns för hur snabbt data kan skickas mellan processorer. Om en processor arbetar med 1 gigahertz kan en signal bara färdas högst cirka 30 centimeter i en enda cykel. Processorer måste därför placeras nära varandra för att minimera kommunikationsfördröjningarna, vilket kan leda till problem med kylningen. Om klockfrekvenserna fortsätter att öka kommer ljusets hastighet så småningom att bli en begränsande faktor för den interna utformningen av enskilda chip.
Relaterade sidor
Frågor och svar
F: Vad är ljusets hastighet?
S: Ljusets hastighet, som betecknas med "c", är en fysikalisk konstant som är exakt 299 792 458 meter per sekund (983 571 056 fot per sekund).
F: Hur representeras ljusets hastighet?
S: Ljusets hastighet betecknas vanligen med "c" och i vakuummedium betecknas den specifikt med "c^0".
F: Vilka partiklar färdas med ljusets hastighet?
S: Fotoner (ljuspartiklar) färdas med denna hastighet i vakuum. Dessutom färdas alla masslösa partiklar som fotoner och tillhörande fält - inklusive elektromagnetisk strålning som ljus - med c oavsett källa eller observatörens tröghetsreferensram.
F: Vad säger den speciella relativitetsteorin om ljusets hastighet?
S: Enligt den speciella relativitetsteorin är c den maximala hastighet med vilken all energi, materia och fysisk information kan färdas i universum. Den säger också att den uppmätta ljushastigheten i ett vakuum förblir oförändrad oavsett om ljuskällan eller observatören rör sig i förhållande till varandra.
F: Hur hänger c samman med tid och rum?
S: I relativitetsteorin kopplar c samman rum och tid genom att det förekommer i Einsteins berömda ekvation E = mc2. Denna ekvation visar hur energi kan omvandlas till massa och vice versa.
F: Finns det några bevis som stöder den speciella relativitetsteorins förutsägelse om den uppmätta ljushastigheten?
S: Ja - hittills har observationer bekräftat denna förutsägelse att oavsett vilken referensram den observeras från eller vilken källa den färdas i - den uppmätta hastigheten förblir konstant.
Sök
