Differentialekvation
En differentialekvation är en matematisk ekvation som innefattar variabler som x eller y, samt den hastighet med vilken dessa variabler förändras. Differentialekvationer är speciella eftersom lösningen på en differentialekvation i sig själv är en funktion i stället för ett tal.
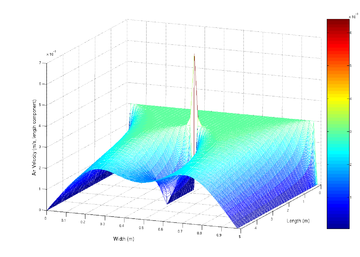
En bild av luftflödet som modelleras med hjälp av en differentialekvation.
Typer av differentialekvationer
Om en differentialekvation endast omfattar x och dess derivata, dvs. den hastighet med vilken x förändras, kallas den för en första ordningens differentialekvation. En differentialekvation av högre ordning har derivat av andra derivat. Om det finns fler variabler än bara x och y sägs det vara en partiell differentialekvation. Ibland lyder något i världen åt flera differentialekvationer samtidigt. Dessa sägs modelleras med hjälp av kopplade differentialekvationer.
Vissa differentialekvationer kan lösas exakt, andra inte. Ibland kan en ekvation bara uppskattas, och ett datorprogram kan göra detta mycket snabbt. Även om de kan verka överdrivet komplicerade för någon som inte har studerat differentialekvationer tidigare, berättar de människor som använder differentialekvationer att de inte skulle kunna räkna ut viktiga saker utan dem. De flesta vetenskapsmän och ingenjörer (liksom matematiker) läser minst en kurs i differentialekvationer när de går i skolan. Vissa matematiker ägnar sin karriär åt att undersöka differentialekvationer som är svåra att lösa.
Använder
Differentialekvationer används inom många vetenskapsområden eftersom de beskriver verkliga saker:
- Inom fysiken för olika former av rörelse eller svängningar.
- Radioaktivt sönderfall beräknas med hjälp av differentialekvationer.
- Isaac Newtons andra rörelselag
- Newtons lag om kylning
- Vågekvationen
- Laplaces ekvation
- Navier-Stokes ekvationer beskrev rörelsen av vätskor.
- Hamiltonekvationer för allmän mekanik
Personer som studerat differentialekvationer
- Carl Gustav Jacob Jacobi
- Hiroshi Umemura
- Israel Gelfand
- Peter Lax
- Ryogo Hirota
- Sofya Kovalevskaya
- Vladimir Arnold
Frågor och svar
F: Vad är en differentialekvation?
S: En differentialekvation är en matematisk ekvation som involverar variabler och deras förändringstakt.
F: Varför är differentialekvationer speciella?
S: Differentialekvationer är speciella eftersom lösningen är en funktion istället för ett tal.
F: Vilken typ av problem hjälper differentialekvationer till att lösa?
S: Differentialekvationer hjälper till att lösa problem där en parameters beroende av en annan är okänd men kan uttryckas som en derivata.
F: Vad är sambandet mellan differentialekvationer och att hitta funktioner?
S: Differentialekvationer hjälper till att hitta en funktion genom dess derivata som är relaterad till andra uttryck.
F: Vilka variabler ingår i en differentialekvation?
S: En differentialekvation innehåller variabler som x eller y och deras förändringstakt.
F: Hur skiljer sig differentialekvationer från vanliga ekvationer?
S: Differentialekvationer skiljer sig från vanliga ekvationer eftersom lösningen är en funktion snarare än ett tal.
F: I vilka situationer kan en differentialekvation vara användbar?
S: Differentialekvationer är användbara i problem där en parameters beroende av en annan är oklart men kan uttryckas som en derivata.
