Gyllene snittet

Med ett tal, nämligen a, och ett annat mindre tal, b, får man kvoten mellan de två talen genom att dividera dem. Deras förhållande är a/b. Ett annat förhållande hittas genom att addera de två talen och dividera detta med det större talet a. Det nya förhållandet är (a+b)/a. Om dessa två förhållanden är lika med samma tal kallas det talet för gyllene snittet. Den grekiska bokstaven φ {\displaystyle \varphi } $\varphi$ (phi) brukar användas som namn för det gyllene snittet.

Till exempel, om b = 1 och a/b = φ {\displaystyle \varphi } $\varphi$ så är a = φ {\displaystyle \varphi } $\varphi$ . Det andra förhållandet (a+b)/a är då ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } $(\varphi +1)/\varphi$ . Eftersom dessa två förhållanden är lika är detta sant:

φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}} $\varphi ={\frac {\varphi +1}{\varphi }}$

Ett sätt att skriva detta tal är

φ = 1 + 5 2 = 1.618... {\displaystyle \varphi ={\frac {1+{{sqrt {5}}}}{2}}}=1.618...} $\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618...$

5 {\displaystyle {\sqrt {5}}}} ${\sqrt {5}}$ är ett tal som när det multipliceras med sig självt ger 5: 5 × 5 = 5 {\displaystyle {\sqrt {5}}}\times {\sqrt {5}}=5} ${\sqrt {5}}\times {\sqrt {5}}=5$ .

Det gyllene snittet är ett irrationellt tal. Det betyder att om en person försöker skriva det, kommer det aldrig att sluta och aldrig att skapa ett mönster, utan det kommer att börja så här: 1.6180339887... En viktig sak med det här talet är att om du drar av 1 från det eller dividerar 1 med det får du samma tal.

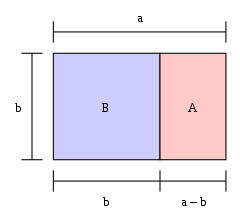
Gyllene rektangel

Om längden på en rektangel dividerad med bredden är lika med det gyllene snittet är rektangeln en "gyllene rektangel". Om en kvadrat skärs av från den ena änden av en gyllene rektangel är den andra änden en ny gyllene rektangel. På bilden är den stora rektangeln (blå och rosa tillsammans) en gyllene rektangel eftersom a/b = φ {\displaystyle a/b=\varphi } $a/b=\varphi$ . Den blå delen (B) är en kvadrat, och den rosa delen för sig själv (A) är en annan gyllene rektangel eftersom b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } $b/(a-b)=\varphi$ . Den stora rektangeln och den rosa rektangeln har samma form, men den rosa rektangeln är mindre och är vänd.

Den stora rektangeln BA är en gyllene rektangel, dvs. förhållandet b:a är 1: φ {\displaystyle \varphi } $\varphi$ . För varje sådan rektangel, och endast för rektanglar med den specifika proportionen, är det som återstår, A, en annan gyllene rektangel, dvs. med samma proportioner som den ursprungliga rektangeln, om vi tar bort kvadrat B.

Fibonacci-tal

Fibonacci-talen är en lista med tal. En person kan hitta nästa nummer i listan genom att addera de två sista numren. Om en person delar ett nummer i listan med det nummer som kom före det, kommer detta förhållande allt närmare det gyllene snittet.

Fibonacci-tal	dividerat med den föregående	Förhållandet
1
1	1/1	= 1.0000
2	2/1	= 2.0000
3	3/2	= 1.5000
5	5/3	= 1.6667
8	8/5	= 1.6000
13	13/8	= 1.6250
21	21/13	= 1.6154...
34	34/21	= 1.6190...
55	55/34	= 1.6177...
89	89/55	= 1.6182...
...	...	...
	φ {\\displaystyle \varphi } $\varphi$	= 1.6180...

Det gyllene snittet i naturen

I naturen används ofta det gyllene snittet för att arrangera blad eller blommor. I dessa används den gyllene vinkeln på cirka 137,5 grader. Blad eller blommor som är arrangerade i den vinkeln utnyttjar solljuset bäst.

Dessutom är avståndet mellan kroppens mittpunkt och golvet och avståndet mellan huvudets topp och ryggradens bas båda i enlighet med det gyllene snittet. Trots att det saknas i vanliga arkitektoniska och designmönster är Leonardo Fibonaccis upptäckt allmänt erkänd som banbrytande. Det kan ta formen av orkaner, elefantbetar, myror, sjöborrar, sjöstjärnor, honungsbin och många andra saker.

Fibonacci-sekvensen börjar med 0 och fortsätter i all oändlighet: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Det finns en summa av två siffror före varje siffra. Själva mönstret är ganska elementärt och oansenligt.

Tills du får veta att detta förhållande ligger bakom skönheten hos Mona Lisa, de mänskliga lemmarna, datakryptering och till och med antalet spiraler på en solrosas huvud. Det verkar som om universum har ett naturligt sätt att hålla reda på siffror.

Blommor har alltid ett udda antal kronblad som överensstämmer med Fibonacci-sekvensen. Till exempel har fredsliljan tre kronblad, smörblommor fem, cikoria 21, prästkragar 34 och så vidare.

Här är några fler naturliga förekomster av det gyllene snittet:

Fröställningar. Blommor producerar frön i sin kärna, som sedan spiralformas utåt och fyller blommans huvud.

Ananas, blomkål och Romanesco-broccoli. Dessa överensstämmer också med Fibonacci-sekvensen.

Tallkottar. Tallkottarna har spiralmönster på sina frökapslar, där två spiraler på varje kotte växer i motsatt riktning när de växer.

Grenar av ett träd. I naturen ses detta mönster när ett träd utvecklar en gren och sedan delar sig i två nya tillväxtpunkter. Sedan kommer bara en av de två nya stammarna att aktivt växa, medan den andra kommer att ligga i vila.

Metoder för fåglars flygning. Hökens bästa angreppsvinkel är vinkelrät mot målets flygbana, vilket är detsamma som spiralens lutning.

Spiralgalaxer. Det finns flera spiralarmar i Vintergatan, var och en med en logaritmisk spiral på omkring 12 grader.

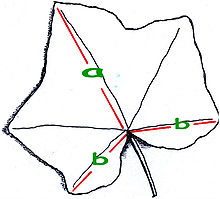
Ett blad av murgröna som visar det gyllene snittet.

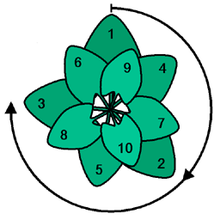
Genom att använda den gyllene vinkeln utnyttjas solens ljus optimalt. Detta är en vy från toppen.

Relaterade sidor

Fibonacci-tal
Phi

Frågor och svar

Fråga: Vad är förhållandet mellan två tal?

S: Förhållandet mellan två tal fås genom att dividera dem, så förhållandet skulle vara a/b.

F: Hur kan man hitta ett annat förhållande?

S: Ett annat förhållande kan hittas genom att addera de två talen och sedan dividera denna summa med det större talet, a. Detta nya förhållande skulle vara (a+b)/a.

Fråga: Vad heter det när dessa två förhållanden är lika stora som varandra?

S: När dessa två förhållanden är lika stora som varandra kallas det gyllene snittet. Det representeras vanligtvis med den grekiska bokstaven צ eller phi.

F: Om b = 1 och a/b = צ , vad betyder det för a?

S: Om b = 1 och a/b = צ , betyder det att a också är צ.

F: Hur kan man på vilket sätt skriva detta tal?

S: Ett sätt att skriva detta tal är צ = 1 + 5 / 2 = 1,618...

F: Vad betyder det om man subtraherar 1 från det eller dividerar 1 med det?

S: Om du subtraherar 1 från det eller dividerar 1 med det får du tillbaka samma tal - med andra ord är båda lika med gyllene snittet.

F: Är det gyllene snittet ett irrationellt tal?

S: Ja, det gyllene snittet är ett irrationellt tal, vilket innebär att om någon försöker skriva ut det, kommer det aldrig att finnas något slut och inget mönster - man kan bara börja med något som "1,6180339887...".